sklearn
特征工程
(Feature Engineering)
特征工程是使用专业背景知识和技巧处理数据**,**使得特征能在机器学习算法上发挥更好的作用的过程
数据集
scikit-learn 提供了一些标准数据集
1
| from sklearn import datasets
|
小规模 load_*()
datasets.load_*()
获取小规模数据集,数据包含在 datasets 里
1
2
| data1 = datasets.load_iris()
data2 = datasets.load_boston()
|
大规模 fetch_*()
datasets.fetch_*(data_home, subset)
获取大规模数据集,需要从网络上下载
- data_home:数据集下载的目录,默认是 ~/scikit_learn_data/
- subset:选择要加载的数据集。’train’或者’test’,‘all’,可选
返回值
load 和 fetch 返回的数据类型为 datasets.base.Bunch (字典继承)
- data:特征数据数组,是二维 numpy.ndarray 数组
- *target:*标签数组,是 n_samples 的一维 numpy.ndarray 数组
- DESCR:数据描述
- feature_names:特征名,新闻数据,手写数字、回归数据集没有
- target_names:标签名
1
2
3
4
5
6
7
8
9
10
11
| from sklearn.datasets import load_iris
# 获取鸢尾花数据集
iris = load_iris()
print("鸢尾花数据集的返回值:\n", iris) # 将所有参数全部返回,返回值是一个继承自字典的Bench
print("鸢尾花的特征值:\n", iris.data)
print("鸢尾花的目标值:\n", iris.target)
print("鸢尾花特征的名字:\n", iris.feature_names)
print("鸢尾花目标值的名字:\n", iris.target_names)
print("鸢尾花的描述:\n", iris.DESCR)
# 同样可以写作诸如iris['data']的格式
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| 鸢尾花的特征值:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
...
[6.3 2.5 5. 1.9]
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
鸢尾花的目标值:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
鸢尾花特征的名字:
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
鸢尾花目标值的名字:
['setosa' 'versicolor' 'virginica']
鸢尾花的描述:
.. _iris_dataset:
Iris plants dataset
--------------------
**Data Set Characteristics:**
:Number of Instances: 150 (50 in each of three classes)
...
- Many, many more ...
|
数据集划分
简单划分 train_test_split
1
| from sklearn.model_selection import train_test_split
|
train_test_split ( arrays, *options )
- x:数据集的特征值
- y:数据集的标签值
- test_size:测试集的大小,一般为 float
- random_state:随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
返回:测试集特征值,测试集标签,训练集特征值,训练集标签(默认随机取)
1
| x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)
|
K 折交叉验证
(KFold Cross Validation)
1
| from sklearn.model_selection import KFold
|
KFold ( n_splits=5, *, shuffle=False, random_state=None )
返回 k 折对象
参数
- n_splits:K 子集个数,int, default=5
- shuffle:是否要洗牌(打乱数据),bool, default=False
- random_state:int or RandomState instance, default=None
方法
- get_n_splits([X, y, groups]):返回迭代次数,Returns the number of splitting iterations in the cross-validator
- split(X):生成器,返回训练和测试集的索引值,Generate indices to split data into training and test set.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| from sklearn.model_selection import KFold
from sklearn import datasets
# 数据集导入
iris = datasets.load_iris()
x = iris.data
y = iris.target
# KFold
kf = KFold(n_splits=5)
# 输出划分数
print(kf.get_n_splits(x))
# 划分数据集
for train_index, test_index in kf.split(x):
print("TRAIN:", train_index, "\nTEST:", test_index)
x_train, x_test = x[train_index], x[test_index]
y_train, y_test = y[train_index], y[test_index]
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
| 5
TRAIN: [ 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65
66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101
102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149]
TEST: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29]
TRAIN: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 26 27 28 29 60 61 62 63 64 65
66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101
102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149]
TEST: [30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59]
TRAIN: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 90 91 92 93 94 95 96 97 98 99 100 101
102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149]
TEST: [60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83
84 85 86 87 88 89]
TRAIN: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89
120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149]
TEST: [ 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107
108 109 110 111 112 113 114 115 116 117 118 119]
TRAIN: [ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71
72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107
108 109 110 111 112 113 114 115 116 117 118 119]
TEST: [120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137
138 139 140 141 142 143 144 145 146 147 148 149]
|
特征抽取
(feature extraction)
将任意数据(如文本或图像)转换为可用于机器学习的数字特征
1
| import sklearn.feature_extraction
|
字典特征提取 DictVectorizer
它是一个转换器,应用时需要进行实例化
API
sklearn.feature_extraction.DictVectorizer(sparse=True,…)
- DictVectorizer.fit_transform(X)
- X:字典或者包含字典的迭代器
- 返回 sparse 矩阵或 array 数组
- DictVectorizer.inverse_transform(X)
- X:array 数组或者 sparse 矩阵
- 返回转换之前数据格式
- DictVectorizer.get_feature_names()
例
流程分析
- 实例化类 DictVectorizer
- 调用 fit_transform 方法输入数据并转换(注意返回格式)
1
2
3
4
5
6
7
8
9
10
11
| from sklearn.feature_extraction import DictVectorizer
data = [{'city': '北京','temperature':100}, {'city': '上海','temperature':60}, {'city': '深圳','temperature':30}]
# 1、实例化一个转换器类
transfer = DictVectorizer(sparse=False)# 拒绝返回稀疏矩阵
# 2、调用fit_transform
data = transfer.fit_transform(data)
print("返回的结果:\n", data)
print("特征名字:\n", transfer.get_feature_names())
|
输出
1
2
3
4
5
6
| 返回的结果:
[[ 0. 1. 0. 100.]
[ 1. 0. 0. 60.]
[ 0. 0. 1. 30.]]
特征名字:
['city=上海', 'city=北京', 'city=深圳', 'temperature']
|
若返回稀疏矩阵,改 sparse=True
1
2
3
4
5
6
7
8
9
| 返回的结果:
(0, 1) 1.0
(0, 3) 100.0
(1, 0) 1.0
(1, 3) 60.0
(2, 2) 1.0
(2, 3) 30.0
特征名字:
['city=上海', 'city=北京', 'city=深圳', 'temperature']
|
这个处理数据的技巧叫做 one-hot 编码
文本词频特征提取 text.CountVectorizer
对文本数据进行词频特征值化
它是一个转换器,应用时需要进行实例化
API
CountVectorizer(stop_words=[])
- CountVectorizer.fit_transform(X)
- X:文本或者包含文本字符串的可迭代对象
- 返回 sparse 矩阵
- CountVectorizer.inverse_transform(X)
- X:array 数组或者 sparse 矩阵
- 返回转换之前数据格
- CountVectorizer.get_feature_names()
例
流程分析
- 实例化类 CountVectorizer
- 调用 fit_transform 方法输入数据并转换 (注意返回格式,利用 toarray() 进行 sparse 矩阵转换 array 数组)
1
2
3
4
5
6
7
8
9
10
11
12
| from sklearn.feature_extraction.text import CountVectorizer
data = ["life is short,i like like python",
"life is too long,i dislike python"]
# 1、实例化一个转换器类
transfer = CountVectorizer()
# 2、调用fit_transform
data = transfer.fit_transform(data)
print("文本特征抽取的结果:\n", data.toarray())
print("返回特征名字:\n", transfer.get_feature_names())
|
输出(因为没有 sparse 参数,若要转换成二维数组形式,需要利用 toarray())
1
2
3
4
5
| 文本特征抽取的结果:
[[0 1 1 2 0 1 1 0]
[1 1 1 0 1 1 0 1]]
返回特征名字:
['dislike', 'is', 'life', 'like', 'long', 'python', 'short', 'too']
|
若直接返回稀疏矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| 文本特征抽取的结果:
(0, 2) 1
(0, 1) 1
(0, 6) 1
(0, 3) 2
(0, 5) 1
(1, 2) 1
(1, 1) 1
(1, 5) 1
(1, 7) 1
(1, 4) 1
(1, 0) 1
返回特征名字:
['dislike', 'is', 'life', 'like', 'long', 'python', 'short', 'too']
|
中文处理
使用 jieba 分词库
jieba.cut()
分析
- 准备句子,利用 jieba.cut 进行分词
- 实例化 CountVectorizer
- 将分词结果变成字符串当作 fit_transform 的输入值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| from sklearn.feature_extraction.text import CountVectorizer
import jieba
def cut_word(text):
# 用结巴对中文字符串进行分词
text = " ".join(list(jieba.cut(text)))
return text
data = ["一种还是一种今天很残酷,明天更残酷,后天很美好,但绝对大部分是死在明天晚上,所以每个人不要放弃今天。",
"我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
# 将原始数据转换成分好词的形式
text_list = []
for sent in data:
text_list.append(cut_word(sent))
print(text_list)
# 1、实例化一个转换器类
transfer = CountVectorizer()
# 2、调用fit_transform
data = transfer.fit_transform(text_list)
print("文本特征抽取的结果:\n", data.toarray())
print("返回特征名字:\n", transfer.get_feature_names())
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
|
['一种 还是 一种 今天 很 残酷 , 明天 更 残酷 , 后天 很 美好 , 但 绝对 大部分 是 死 在 明天 晚上 , 所以 每个 人 不要 放弃 今天 。', '我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 , 这样 当 我们 看到 宇宙 时 , 我们 是 在 看 它 的 过去 。', '如果 只用 一种 方式 了解 某样 事物 , 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。']
文本特征抽取的结果:
[[2 0 1 0 0 0 2 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 2 0 1 0 2 1 0 0 0 1 1 0 0 1
0]
[0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0 1 3 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 1 0
1]
[1 1 0 0 4 3 0 0 0 0 1 1 0 1 0 1 1 0 1 0 0 1 0 0 0 1 0 0 0 2 1 0 0 1 0 0
0]]
返回特征名字:
['一种', '不会', '不要', '之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '还是', '这样']
|
Tf-idf 文本特征提取 text.TfidfVectorizer
TF-IDF 的主要思想是:如果某个词或短语在一篇文章中出现的概率高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。
TF-IDF 作用:用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。
公式
- 词频(term frequency,tf)指的是某一个给定的词语在该文件中出现的频率
- 逆向文档频率(inverse document frequency,idf)是一个词语普遍重要性的度量。由总文件数目除以包含该词语之文件的数目,再将得到的商取以 10 为底的对数得到
$$
tfidf_{i,j}=tf_{i,j}\times idf_i
$$
假如一篇文件的总词语数是 100 个,而词语"非常"出现了 5 次,那么"非常"一词在该文件中的词频就是5/100=0.05。而计算文件频率(IDF)的方法是以文件集的文件总数,除以出现"非常"一词的文件数。所以,如果"非常"一词在1,000份文件出现过,而文件总数是 10,000,000 份的话,其逆向文件频率就是 lg(10,000,000 / 1,0000)=3。最后"非常"对于这篇文档的tf-idf的分数为0.05 * 3=0.15
API
TfidfVectorizer(stop_words=[])
- TfidfVectorizer.fit_transform(X)
- X:文本或者包含文本字符串的可迭代对象
- 返回 sparse 矩阵
- TfidfVectorizer.inverse_transform(X)
- X:array 数组或者 sparse 矩阵
- 返回转换之前数据格
- TfidfVectorizer.get_feature_names()
例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| from sklearn.feature_extraction.text import TfidfVectorizer
import jieba
def cut_word(text):
# 用结巴对中文字符串进行分词
text = " ".join(list(jieba.cut(text)))
return text
data = ["一种还是一种今天很残酷,明天更残酷,后天很美好,但绝对大部分是死在明天晚上,所以每个人不要放弃今天。",
"我们看到的从很远星系来的光是在几百万年之前发出的,这样当我们看到宇宙时,我们是在看它的过去。",
"如果只用一种方式了解某样事物,你就不会真正了解它。了解事物真正含义的秘密取决于如何将其与我们所了解的事物相联系。"]
# 将原始数据转换成分好词的形式
text_list = []
for sent in data:
text_list.append(cut_word(sent))
print(text_list)
# 1、实例化一个转换器类
transfer = TfidfVectorizer(stop_words=['一种', '不会', '不要'])
# 2、调用fit_transform
data = transfer.fit_transform(text_list)
print("文本特征抽取的结果:\n", data.toarray())
print("返回特征名字:\n", transfer.get_feature_names())
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| ['一种 还是 一种 今天 很 残酷 , 明天 更 残酷 , 后天 很 美好 , 但 绝对 大部分 是 死 在 明天 晚上 , 所以 每个 人 不要 放弃 今天 。', '我们 看到 的 从 很 远 星系 来 的 光是在 几百万年 之前 发出 的 , 这样 当 我们 看到 宇宙 时 , 我们 是 在 看 它 的 过去 。', '如果 只用 一种 方式 了解 某样 事物 , 你 就 不会 真正 了解 它 。 了解 事物 真正 含义 的 秘密 取决于 如何 将 其 与 我们 所 了解 的 事物 相 联系 。']
文本特征抽取的结果:
[[0. 0. 0. 0.43643578 0. 0.
0. 0. 0. 0.21821789 0. 0.21821789
0. 0. 0. 0. 0.21821789 0.21821789
0. 0.43643578 0. 0.21821789 0. 0.43643578
0.21821789 0. 0. 0. 0.21821789 0.21821789
0. 0. 0.21821789 0. ]
[0.2410822 0. 0. 0. 0.2410822 0.2410822
0.2410822 0. 0. 0. 0. 0.
0. 0. 0.2410822 0.55004769 0. 0.
0. 0. 0.2410822 0. 0. 0.
0. 0.48216441 0. 0. 0. 0.
0. 0.2410822 0. 0.2410822 ]
[0. 0.644003 0.48300225 0. 0. 0.
0. 0.16100075 0.16100075 0. 0.16100075 0.
0.16100075 0.16100075 0. 0.12244522 0. 0.
0.16100075 0. 0. 0. 0.16100075 0.
0. 0. 0.3220015 0.16100075 0. 0.
0.16100075 0. 0. 0. ]]
返回特征名字:
['之前', '了解', '事物', '今天', '光是在', '几百万年', '发出', '取决于', '只用', '后天', '含义', '大部分', '如何', '如果', '宇宙', '我们', '所以', '放弃', '方式', '明天', '星系', '晚上', '某样', '残酷', '每个', '看到', '真正', '秘密', '绝对', '美好', '联系', '过去', '还是', '这样']
|
特征预处理
(feature preprocessing)
通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程
数据的无量纲处理:使不同规格的数据转换到同一规格
特征的单位或者大小相差较大,或者某特征的方差相比其他的特征要大出几个数量级**,**容易影响(支配)目标结果,使得一些算法无法学习到其它的特征,所以要进行归一化/标准化。
1
| import sklearn.preprocessing
|
归一化
通过对原始数据进行变换把数据映射到(默认为)[0,1] 之间
公式
$$
X’=\cfrac{x-min}{max-min}\
X’’=X’*(mx-mi)+mi
$$
作用于每一列,max 为一列的最大值,min 为一列的最小值,X’’为最终结果,mx,mi分别为指定区间值,默认mx为1,mi为0
API
MinMaxScaler (feature_range=(0,1)… )
- MinMaxScalar.fit_transform(X)
- X:numpy array 格式的数据 [n_samples,n_features]
- 返回值:转换后的形状相同的 array
例
以下为数据实例
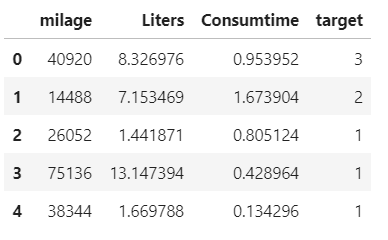
实例化 MinMaxScalar
通过 fit_transform 转换
1
2
3
4
5
6
7
8
9
10
11
12
| from sklearn.preprocessing import MinMaxScaler
import pandas as pd
path = "../Data/Dating.txt"
data = pd.read_csv(path)
# 1、实例化一个转换器类
transfer = MinMaxScaler(feature_range=(0, 1)) # 默认 MIN=0, MAX=1
# 2、调用fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']]) # 需要传numpy array格式, 返回array
print("最小值最大值归一化处理的结果:\n", data)
|
输出
1
2
3
4
5
6
| 最小值最大值归一化处理的结果:
[[0.43582641 0.58819286 0.53237967]
[0. 0.48794044 1. ]
[0.19067405 0. 0.43571351]
[1. 1. 0.19139157]
[0.3933518 0.01947089 0. ]]
|
注意最大值最小值是变化的,另外,最大值与最小值非常容易受异常点影响,所以这种方法鲁棒性较差,只适合传统精确小数据场景
标准化
通过对原始数据进行变换把数据变换到均值为 0,标准差为 1 的范围内
优势
- 对于归一化来说:如果出现异常点,影响了最大值和最小值,那么结果显然会发生改变
- 对于标准化来说:如果出现异常点,由于具有一定数据量,少量的异常点对于平均值的影响并不大,从而方差改变较小
公式
$$
X’=\cfrac{x-mean}{\sigma}
$$
作用于每一列,mean 为平均值,σ 为标准差
API
StandardScaler( )
- StandardScaler.fit_transform(X)
- X:numpy array 格式的数据
[n_samples, n_features] - 返回值:转换后的形状相同的 array
- StandardScaler.mean_
- StandardScaler.var_
例
同样对 2.4.1 的数据进行处理
实例化 StandardScaler
通过 fit_transform 转换
1
2
3
4
5
6
7
8
9
10
11
12
13
| import pandas as pd
from sklearn.preprocessing import StandardScaler
data = pd.read_csv(path)
# 1、实例化一个转换器类
transfer = StandardScaler() # 值都在0附近,所以有负数是正常的
# 2、调用fit_transform
data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
print("标准化的结果:\n", data)
print("每一列特征的平均值:\n", transfer.mean_)
print("每一列特征的方差:\n", transfer.var_)
|
输出
1
2
3
4
5
6
7
8
9
10
| 标准化的结果:
[[ 0.0947602 0.44990013 0.29573441]
[-1.20166916 0.18312874 1.67200507]
[-0.63448132 -1.11527928 0.01123265]
[ 1.77297701 1.54571769 -0.70784025]
[-0.03158673 -1.06346729 -1.27113187]]
每一列特征的平均值:
[3.8988000e+04 6.3478996e+00 7.9924800e-01]
每一列特征的方差:
[4.15683072e+08 1.93505309e+01 2.73652475e-01]
|
特征降维
(Feature Dimension Reduce)
降维是指在某些限定条件下,降低随机变量(特征)个数,得到一组“不相关”主变量的过程
两种方式
特征选择
1
| import sklearn.feature_selection
|
数据中包含冗余或无关变量(或称特征、属性、指标等),旨在从原有特征中找出主要特征
方法
- 过滤式(Filter):主要探究特征本身特点、特征与特征和目标值之间关联
- 嵌入式(Embedded):算法自动选择特征(特征与目标值之间的关联)
- 决策树:信息熵、信息增益
- 正则化:L1、L2
- 深度学习:卷积等
低方差特征过滤
删除低方差的一些特征
API
VarianceThreshold(threshold = 0.0)
- Variance.fit_transform(X)
- X:numpy array 格式的数据 [n_samples, n_features]
- 返回值:训练集差异低于 threshold 的特征将被删除。默认值是保留所有非零方差特征,即删除所有样本中具有相同值的特征。
例
处理以下例子

分析
1
2
3
4
5
6
7
8
9
10
11
12
13
| from sklearn.feature_selection import VarianceThreshold
import pandas as pd
path="../Data/Dating.txt"
data = pd.read_csv(path)
# 1、实例化一个转换器类
transfer = VarianceThreshold(threshold=1)
# 2、调用fit_transform
data = transfer.fit_transform(data.iloc[:, 0:-1])
print("删除低方差特征的结果:\n", data)
print("形状:\n", data.shape)
|
输出
1
2
3
4
5
6
7
8
| 删除低方差特征的结果:
[[4.0920000e+04 8.3269760e+00]
[1.4488000e+04 7.1534690e+00]
[2.6052000e+04 1.4418710e+00]
[7.5136000e+04 1.3147394e+01]
[3.8344000e+04 1.6697880e+00]]
形状:
(5, 2)
|
相关系数
去除相关特征(correlated feature)的影响
使用 Scipy 实现
1
| from scipy.stats import pearsonr
|
原理
皮尔逊相关系数(Pearson Correlation Coefficient):反映变量之间相关关系密切程度的统计指标
$$
r=\cfrac{n\sum xy=\sum x\sum y}{\sqrt{n\sum x^2 -(\sum x)^2}\sqrt{n\sum y^2-(\sum y)^2}}
$$
相关系数的值介于–1 与+1 之间,即–1≤ r ≤+1。其性质如下:
- 当 r > 0 时,表示两变量正相关,r < 0 时,两变量为负相关
- 当|r|=1 时,表示两变量为完全相关,当 r=0 时,表示两变量间无相关关系
- 当 0<|r|<1 时,表示两变量存在一定程度的相关。且|r|越接近 1,两变量间线性关系越密切;|r|越接近于 0,表示两变量的线性相关越弱
- 一般可按三级划分:|r|<0.4 为低度相关;0.4≤|r|<0.7 为显著性相关;0.7≤|r|<1 为高度线性相关
API
pearsonr(X, Y)
- X:numpy array 格式的数据
- Y:numpy array 格式的数据
- 返回值
- r:相关系数 [-1,1] 之间
- p-value:p 值(p 值越小,表示相关系数越显著,一般 p 值在 500 个样本以上时有较高的可靠性)
如果相关性高可用以下方法:
选取其中一个特征
两个特征加权求和
主成分分析(高维数据变低维,舍弃原由数据,创造新数据,如:压缩数据维数,降低原数据复杂度,损失少了信息)
例
两两特征之间进行相关性计算
1
2
3
4
5
6
7
8
9
10
11
12
| from scipy.stats import pearsonr
import pandas as pd
path="../Data/Dating.txt"
data = pd.read_csv(path)
# 皮尔逊相关系数范围[-1,1], 如果大于0就是正相关(越接近1就越相关), 反之亦然
r = pearsonr(data["milage"], data["Liters"])
print("milage和Liters的相关系数为:\n", r)
r = pearsonr(data["milage"], data["Consumtime"])
print("milage和Liters的相关系数为:\n", r)
|
输出
1
2
3
4
| milage和Liters的相关系数为:
(0.660861943290103, 0.2246299034335304)
milage和Liters的相关系数为:
(-0.6406267138718624, 0.2441916485876286)
|
主成分分析
(PCA)将数据分解为较低维数空间
1
| from sklearn.decomposition import PCA
|
概念
- 定义:高维数据转化为低维数据的过程,在此过程中可能会舍弃原有数据、创造新的变量
- 作用:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息
- 应用:回归分析或者聚类分析当中
API
PCA(n_components=None)
参数:n_components
- 小数:表示保留百分之多少的信息
- 整数:减少到多少特征
PCA.fit_transform(X)
- X:numpy array 格式的数据 [n_samples,n_features]
- 返回值:转换后指定维度的 array
例
1
2
3
4
5
6
7
| from sklearn.decomposition import PCA
data = [[2, 8, 4, 5], [3, 8, 5, 5], [10, 5, 1, 0]] # 3*4矩阵 包含四个特征
transfer = PCA(n_components=3) # 为整数就是转为多少个特征 保留的至少都比原特征值少一个
data_new = transfer.fit_transform(data)
print("(主成分分析)PCA降维:\n", data_new)
|
输出
1
2
3
4
| (主成分分析)PCA降维:
[[-3.57495904e+00 -6.64748145e-01 1.07947657e-16]
[-3.17447323e+00 6.91574499e-01 1.07947657e-16]
[ 6.74943227e+00 -2.68263539e-02 1.07947657e-16]]
|
若 n_components 设为 0.95
1
2
3
4
| (主成分分析)PCA降维:
[[-3.57495904]
[-3.17447323]
[ 6.74943227]]
|
转换器和估计器
转换器
(transformer)
特征工程的接口称之为转换器;转换器是特征工程的父类
调用步骤
实例化 (实例化的是一个转换器类(Transformer))
调用 fit_transform(对于文档建立分类词频矩阵,不能同时调用)
转换器调用形式
- fit_transform()
- fit()
- transform()
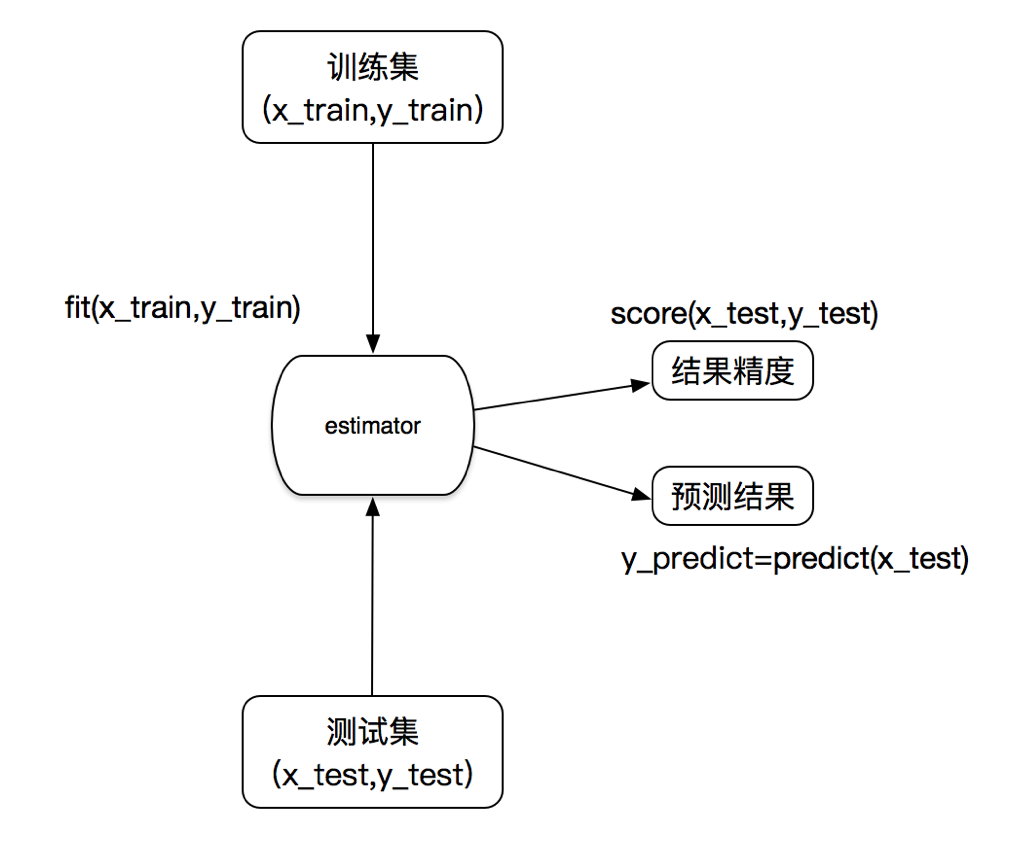
估计器
(estimator)
估计器实现了算法的 API,估计器是算法的父类
- 用于分类的估计器:
- sklearn.neighbors k-近邻算法
- sklearn.naive_bayes 贝叶斯
- sklearn.linear_model.LogisticRegression 逻辑回归
- sklearn.tree 决策树与随机森林
- 用于回归的估计器:
- sklearn.linear_model.LinearRegression 线性回归
- sklearn.linear_model.Ridge 岭回归
- 用于无监督学习的估计器
- sklearn.cluster.KMeans 聚类
调用步骤
实例化估计器类 estimator
进行训练,一旦调用完毕,意味着模型生成
- estimator.fit(x_train, y_train)
模型评估
模型选择与调优
1
| from sklearn.model_selection import GridSearchCV
|
概念
交叉验证
(cross validation)
将拿到的训练数据,分为训练和验证集
超参数搜索-网格搜索
(Grid Search)
通常情况下,有很多参数是需要手动指定的(如 k-近邻算法中的 K 值),这种叫超参数。但是手动过程繁杂,所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
API
GridSearchCV(estimator, param_grid=None,cv=None)
对估计器的指定参数值进行详尽搜索
- 参数
- estimator:估计器对象
- param_grid:估计器参数
(dict){“n_neighbors”:[1,3,5]} - cv:指定几折交叉验证
- 方法
- 结果分析:
- best_params_:在交叉验证中验证的最好超参数
- best_score_:在交叉验证中验证的最好结果
- best_estimator_:最好的参数模型
- cv_results_:每次交叉验证后的验证集准确率结果和训练集准确率结果
分类的评估方法
分类评估报告 API
1
| from sklearn.metrics import classification_report
|
classification_report(y_true, y_pred, labels=[], target_names=None )
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字
- target_names:目标类别名称
- return:每个类别精确率与召回率
ROC 曲线与 AUC 指标
1
| from sklearn.metrics import roc_auc_score
|
- AUC 只能用来评价二分类
- AUC 非常适合评价样本不平衡中的分类器性能
TPR 与 FPR
- TPR = TP / (TP + FN)
- 所有真实类别为 1 的样本中,预测类别为 1 的比例
- 即为召回率(查全率)
- FPR = FP / (FP + FN)
- 所有真实类别为 0 的样本中,预测类别为 1 的比例
ROC 曲线
- ROC 曲线的横轴就是 FPRate,纵轴就是 TPRate,当二者相等时,表示的意义则是:对于不论真实类别是 1 还是 0 的样本,分类器预测为 1 的概率是相等的,此时 AUC 为 0.5
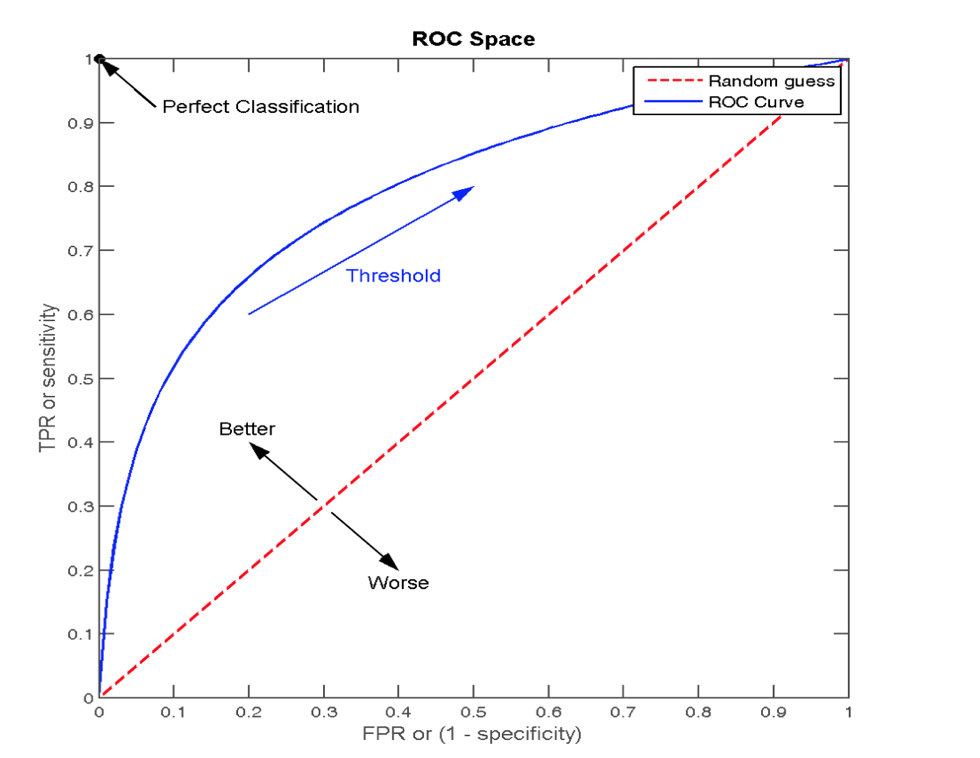
AUC 指标
- AUC 的概率意义是随机取一对正负样本,正样本得分大于负样本的概率
- AUC 的最小值为 0.5,最大值为 1,取值越高越好
- AUC=1,完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器(模型)妥善设定阈值的话,能有预测价值。
最终AUC的范围在 [0.5, 1] 之间,并且越接近1越好
API
roc_auc_score(y_true, y_score)
- 计算 ROC 曲线面积,即 AUC 值
- y_true:每个样本的真实类别,必须为 0 (反例), 1 (正例)标记
- y_score:每个样本预测的概率值
模型保存和加载
- 保存:joblib.dump( estimator, ‘XXX.pkl’ )
- 加载:estimator = joblib.load( ‘XXX.pkl’ )
例
1
2
3
4
5
6
7
8
9
10
| import joblib
def store_model(estimator, name):
joblib.dump(estimator, "../../models/"+name)
return "SUCCESS"
def load_model(name):
model = joblib.load("../../models/"+name)
return model
|
分类
KNN 算法
根据邻居,判断类别
1
| from sklearn.neighbors import KNeighborsClassifier
|
(K Nearest Neighbor)即 K - 近邻算法
如果一个样本在特征空间中的 k 个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
- 优点:
- 缺点:
- 懒惰算法,对测试样本分类时的计算量大,内存开销大
- 必须指定 K 值,K 值选择不当则分类精度不能保证
- 使用场景:小数据场景,几千~几万样本,具体场景具体业务去测试
API
KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
- n_neighbors:int,可选(默认= 5),使用的邻居数
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选用于计算最近邻居的算法,不同实现方式影响效率
- ‘ball_tree’ 将会使用 BallTree
- ‘kd_tree’ 将使用 KDTree
- ‘auto’ 将尝试根据传递给 fit 方法的值来决定最合适的算法
例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn import datasets
import numpy as np
import pandas as pd
# 数据集导入
iris = datasets.load_iris()
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=43)
# 标准化
transfer_std = StandardScaler()
x_train_std = transfer_std.fit_transform(x_train)
x_test_std = transfer_std.transform(x_test) # 测试集不要用fit, 因为要保持和训练集处理方式一致
# KNN
estimator_knn = KNeighborsClassifier(n_neighbors=3)
# 调优
param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
estimator_knn = GridSearchCV(
estimator_knn, param_grid=param_dict, cv=10) # 10折
# 训练模型
estimator_knn.fit(x_train_std, y_train)
y_pred = estimator_knn.predict(x_test_std)
print("预测值为:", y_pred, "\n真实值为:", y_test, "\n比较结果为:", y_test == y_pred)
print("准确率为:\n", estimator_knn.score(x_test_std, y_test))
print("最佳参数:\n", estimator_knn.best_params_)
print("最佳结果:\n", estimator_knn.best_score_)
print("最佳估计器:\n", estimator_knn.best_estimator_)
print("交叉验证结果:\n", estimator_knn.cv_results_)
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| 预测值为: [0 0 2 1 2 0 2 1 1 1 0 1 2 0 1 1 0 0 2 2 0 0 0 1 2 2 0 1 0 0 1 0 1 1 2 2 1
2]
真实值为: [0 0 2 1 2 0 2 1 1 1 0 1 2 0 1 1 0 0 2 2 0 0 0 2 2 2 0 1 0 0 1 0 1 1 2 2 1
2]
比较结果为: [ True True True True True True True True True True True True
True True True True True True True True True True True False
True True True True True True True True True True True True
True True]
准确率为:
0.9736842105263158
最佳参数:
{'n_neighbors': 1}
最佳结果:
0.9469696969696969
最佳估计器:
KNeighborsClassifier(n_neighbors=1)
交叉验证结果:
{'mean_fit_time': array([0.00029657, 0.00039995, 0.00039968, 0.00049977, 0.00029998,
0.00040131]), 'std_fit_time': array([0.00045309, 0.00048983, 0.00048951, 0.00049977, 0.00045822,
0.0004915 ]), 'mean_score_time': array([0.00089977, 0.00080023, 0.00110025, 0.00080018, 0.00079889,
0.00080283]), 'std_score_time': array([0.00029992, 0.0004004 , 0.00030082, 0.00040009, 0.00039965,
0.00040154]), 'param_n_neighbors': masked_array(data=[1, 3, 5, 7, 9, 11],
mask=[False, False, False, False, False, False],
fill_value='?',
dtype=object), 'params': [{'n_neighbors': 1}, {'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 7}, {'n_neighbors': 9}, {'n_neighbors': 11}], 'split0_test_score': array([0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667]), 'split1_test_score': array([0.91666667, 0.91666667, 0.83333333, 0.91666667, 0.91666667,
0.91666667]), 'split2_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
1. ]), 'split3_test_score': array([0.90909091, 0.90909091, 0.90909091, 0.90909091, 0.90909091,
0.81818182]), 'split4_test_score': array([1., 1., 1., 1., 1., 1.]), 'split5_test_score': array([0.90909091, 0.90909091, 1. , 1. , 1. ,
1. ]), 'split6_test_score': array([1., 1., 1., 1., 1., 1.]), 'split7_test_score': array([0.90909091, 0.81818182, 0.81818182, 0.81818182, 0.81818182,
0.81818182]), 'split8_test_score': array([1., 1., 1., 1., 1., 1.]), 'split9_test_score': array([1. , 0.90909091, 1. , 1. , 1. ,
0.90909091]), 'mean_test_score': array([0.9469697 , 0.92878788, 0.93863636, 0.9469697 , 0.9469697 ,
0.93787879]), 'std_test_score': array([0.04338734, 0.05412294, 0.06830376, 0.05945884, 0.05945884,
0.07048305]), 'rank_test_score': array([1, 6, 4, 1, 1, 5])}
|
朴素贝叶斯算法
(Naive Bayes)
相互独立的特征 + 贝叶斯公式
1
| from sklearn.naive_bayes import MultinomialNB
|
朴素:特征与特征之间是相互独立的
朴素贝叶斯算法经常用于文本分类, 因为文章转换成机器学习算法识别的数据是以单词为特征的
- 优点:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
- 分类准确度高,速度快
- 缺点:
- 由于使用了样本属性独立性的假设,所以如果特征属性有关联时其效果不好
原理
贝叶斯公式
以文本分类为例
$$
P(C|F_1,F_2,\ldots)=\cfrac{P(F_1,F_2,\ldots|C)P(C)}{P(F_1,F_2,\ldots)}
$$
- $P(C)$:每个文档类别的概率(某文档类别数/总文档数量)
- $P(W│C)$:给定类别下特征(被预测文档中出现的词)的概率
- $W$ 为给定文档的特征值(频数统计)
- 计算方法:$P(F_1│C)=N_i/N$ (训练文档中去计算)
- $N_i$:该 $F_1$ 词在 $C$ 类别所有文档中出现的次数
- $N$:所属类别 $C$ 下的文档的文本总和
- $P(F_1,F_2,\ldots)$ 预测文档中每个词的概率
拉普拉斯平滑系数
目的:防止计算出的分类概率为 0
$$
P(F_1|C)=\cfrac{N_i+\alpha}{N+\alpha m}
$$
- $\alpha$:预先指定的系数,默认为 1
- $m$:训练文档中特征词的种类数
1
2
3
4
| # 因为样本数量不够,会出现特征词不在一类文本中出现的情况
P(娱乐|影院,支付宝,云计算) = 𝑃(影院,支付宝,云计算|娱乐)∗P(娱乐)=(56/121)∗(15/121)∗(0/121)∗(60/90) = 0
# 此时需要实用到拉普拉斯平滑系数
P(娱乐|影院,支付宝,云计算) =P(影院,支付宝,云计算|娱乐)P(娱乐)=(56+1/121+4)(15+1/121+4)(0+1/121+1*4)(60/90) = 0.00002
|
API
MultinomialNB(alpha = 1.0)
例:20类新闻分类
分析
- 划分数据集
- tfidf 进行的特征抽取
- 朴素贝叶斯预测
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| from sklearn.datasets import fetch_20newsgroups, load_files
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
import pandas as pd
data = fetch_20newsgroups(subset="all")
x_train, x_test, y_train, y_test = \
train_test_split(data.data, data.target, test_size=0.2, random_state=22)
# 文本分类
transfer = TfidfVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 朴素贝叶斯
estimator = MultinomialNB()
estimator.fit(x_train, y_train)
y_predict = estimator.predict(x_test)
print("预测值为:", y_predict, "\n真实值为:", y_test, "\n比较结果为:", y_test == y_predict)
score = estimator.score(x_test, y_test)
print("准确率为: ", score)
|
输出
1
2
3
4
| 预测值为: [15 13 16 ... 13 2 13]
真实值为: [15 13 16 ... 13 2 13]
比较结果为: [ True True True ... True True True]
准确率为: 0.8511936339522547
|
决策树
(Decision Tree)
1
| from sklearn.tree import DecisionTreeClassifier
|
if - else 根据特征的信息熵筛选
原理
信息熵
$$
H(X)=-\sum\limits_{i=1}^n P(x_i)log_bP(x_i)
$$
条件信息熵
$$
H(D|A)=\sum\limits_{i=1}^n \cfrac{|D_i|}{|D|}H(D_i)
$$
信息增益
决策树的划分依据之一
特征 $A$ 对训练数据集 $D$ 的信息增益 $g(D,A)$,定义为集合 D 的信息熵 $H(D)$ 与特征 $A$ 给定条件下 $D$ 的信息条件熵 $H(D|A)$ 之差
$$
g(D,A)=H(D)=H(D|A)
$$
三种算法实现
- ID3
- C4.5
- CART
- 分类树: 基尼系数 最小的准则 在 sklearn 中可以选择划分的默认原则
- 优势:划分更加细致(从后面例子的树显示来理解)
API
DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)
决策树分类器
- criterion:默认是 ’gini’ 系数,也可以选择信息增益的熵 ’entropy’
- max_depth:树的深度大小
- random_state:随机数种子
保存树的结构
1
| from sklearn.tree import export_graphviz
|
export_graphviz()
该函数能够导出 DOT 格式
- tree.export_graphviz(estimator, out_file=path, feature_names)
例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
iris = datasets.load_iris()
x_train, x_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=22)
# 决策树训练
estimator = DecisionTreeClassifier(criterion="entropy")
estimator.fit(x_train, y_train)
# 生成树文件
export_graphviz(estimator, out_file="tree.dot",
feature_names=iris.feature_names)
y_pred = estimator.predict(x_test)
print("预测值为:", y_pred, "\n真实值为:", y_test, "\n比较结果为:", y_test == y_pred)
score = estimator.score(x_test, y_test)
print("准确率为: ", score)
|
输出
1
2
3
4
5
6
7
8
9
| 预测值为: [0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 1 0 0 1 1 1 0 0
0]
真实值为: [0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 2 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
比较结果为: [ True True True True True True True False True True True True
True True True True True True False True True True True True
True True True True True False True True True True True True
True True]
准确率为: 0.9210526315789473
|
随机森林
1
| from sklearn.ensemble import RandomForestClassifier
|
随机森林是一个包含多个决策树的分类器,并且其输出的类别是由个别树输出的类别的众数而定。
原理
学习算法根据下列算法而建造每棵树
- 用 N 来表示 样本个数,M 表示特征数目。
- 1、有放回地抽样(bootstrap),一次随机选出一个样本,重复 N 次
- 2、随机选出 m 个特征, m «M,建立决策树
API
RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, bootstrap=True, random_state=None, min_samples_split=2)
随机森林分类器
n_estimators:integer,optional(default = 10)森林里的树木数量 120,200,300,500,800,1200
criteria:string,可选(default =“gini”)分割特征的测量方法
max_depth:integer 或 None,可选(默认=无)树的最大深度 5,8,15,25,30
max_features=“auto”:每个决策树的最大特征数量
- If “auto”, then
max_features=sqrt(n_features). - If “sqrt”, then
max_features=sqrt(n_features) (same as “auto”). - If “log2”, then
max_features=log2(n_features). - If None, then
max_features=n_features.
bootstrap:boolean,optional(default = True)是否在构建树时使用放回抽样
min_samples_split:节点划分最少样本数
min_samples_leaf:叶子节点的最小样本数
超参数:n_estimator, max_depth, min_samples_split,min_samples_leaf
例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
iris = datasets.load_iris()
# 数据集划分
x_train, x_test, y_train, y_test = train_test_split(
iris.data, iris.target, random_state=22)
# RandomForest
estimator_rf = RandomForestClassifier()
# 超参调优
param_dict = {"n_estimators": [120,200,300,500,800,1200], "max_depth": [5, 8, 15, 25, 30]}
estimator_rf = GridSearchCV(estimator_rf, param_grid=param_dict,cv=5)
# 训练
estimator_rf.fit(x_train,y_train)
y_pred = estimator_rf.predict(x_test)
# 输出结果
print("预测值为:", y_pred, "\n真实值为:", y_test, "\n比较结果为:", y_test == y_pred)
print("准确率为:\n", estimator_rf.score(x_test, y_test))
print("最佳参数:\n", estimator_rf.best_params_)
print("最佳结果:\n", estimator_rf.best_score_)
print("最佳估计器:\n", estimator_rf.best_estimator_)
print("交叉验证结果:\n", estimator_rf.cv_results_)
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| 预测值为: [0 2 1 2 1 1 1 1 1 0 2 1 2 2 0 2 1 1 1 1 0 2 0 1 2 0 2 2 2 1 0 0 1 1 1 0 0
0]
真实值为: [0 2 1 2 1 1 1 2 1 0 2 1 2 2 0 2 1 1 2 1 0 2 0 1 2 0 2 2 2 2 0 0 1 1 1 0 0
0]
比较结果为: [ True True True True True True True False True True True True
True True True True True True False True True True True True
True True True True True False True True True True True True
True True]
准确率为:
0.9210526315789473
最佳参数:
{'max_depth': 5, 'n_estimators': 120}
最佳结果:
0.9553571428571429
最佳估计器:
RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
max_depth=5, max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=120, n_jobs=1,
oob_score=False, random_state=None, verbose=0,
warm_start=False)
交叉验证结果:
{'mean_fit_time': array([0.32009826, 0.57197742, ......., 0., 0., 0., 0.])}
|
逻辑回归
(Logistic Regression)
1
| from sklearn.linear_model import LogisticRegression
|
逻辑回归是机器学习中的一种分类模型,逻辑回归是一种分类算法,虽然名字中带有回归,但是它与回归之间有一定的联系。
原理
输入
逻辑回归的输入就是一个线性回归的结果。
$$
h(w)=w_1x_1+w_2x_2+w_3x_3\ldots+b
$$
激活函数
sigmoid 函数
$$
g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}
$$
分析
- 回归的结果输入到 sigmoid 函数当中
- 输出结果:[0, 1] 区间中的一个概率值,默认为 0.5 为阈值
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为 1 (正例),另外的一个类别会标记为 0 (反例)。(方便损失计算)
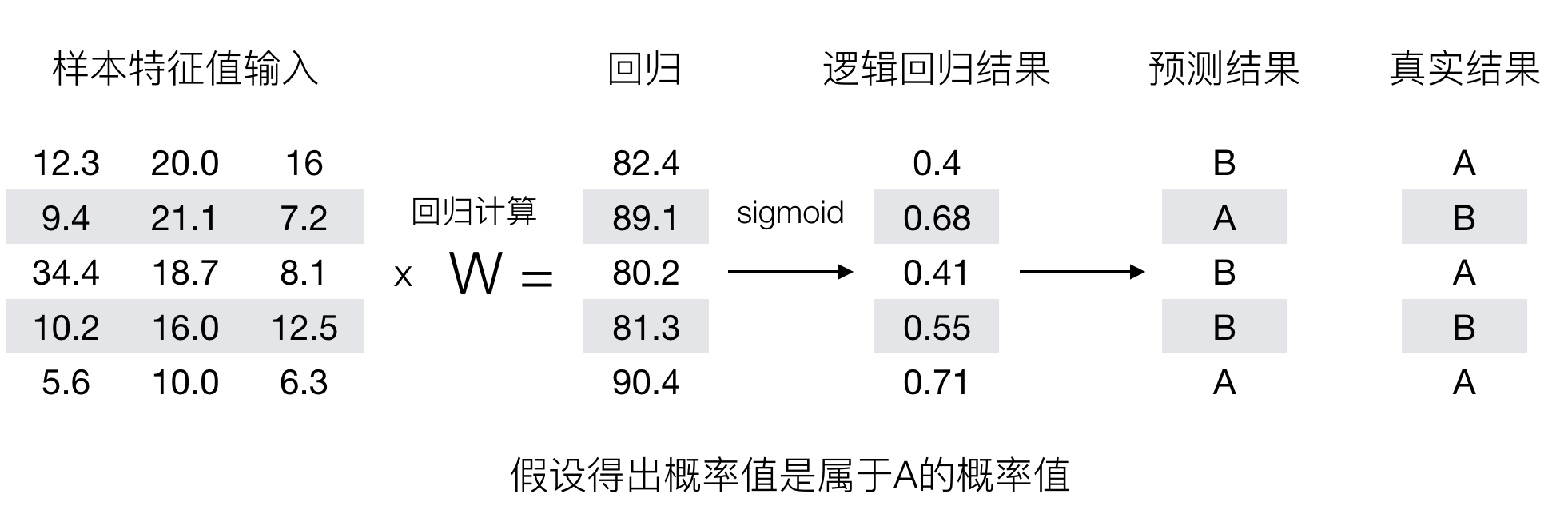
损失函数
逻辑回归的损失,称之为对数似然损失
$$
cost(h_\theta(x),y)=\sum\limits_{i=1}^m-y_ilog(h_\theta(x))-(1-y_i)log(1-h_\theta(x))
$$

优化
同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于 1 类别的概率,降低原本是 0 类别的概率。
API
LogisticRegression(solver=‘liblinear’, penalty=‘l2’, C = 1.0)
- solver:优化求解方式(默认开源的 liblinear 库实现,内部使用了坐标轴下降法来迭代优化损失函数)
- penalty:正则化的种类
- C:正则化力度
LogisticRegression 方法相当于 SGDClassifier(loss="log", penalty=" "), SGDClassifier 实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置 average=True。而使用 LogisticRegression (实现了 SAG)
例
案例:癌症分类预测-良/恶性乳腺癌肿瘤预测
数据描述
(1)699条样本,共11列数据,第一列用语检索的id,后9列分别是与肿瘤
相关的医学特征,最后一列表示肿瘤类型的数值。
(2)包含16个缺失值,用 ”?” 标出。
分析
初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report, roc_auc_score, roc_curve
import matplotlib.pyplot as plt
# 文件读取
column_name = ['Sample code number', 'Clump Thickness',
'Uniformity of Cell Size', 'Uniformity of Cell Shape', 'Marginal Adhesion',
'Single Epithelial Cell Size',
'Bare Nuclei', 'Bland Chromatin',
'Normal Nucleoli', 'Mitoses', 'Class']
original_data = pd.read_csv('../Data/breast-cancer-wisconsin.data',names=column_name)
original_data.head()
# 缺失值处理
# 第一步先替换 ? 为 nan
data = original_data.replace(to_replace="?", value=np.nan)
data.dropna(inplace=True)
print("检测是否还有缺失值(全为false表示没有缺失值)") # 检测是否还有缺失值
print(data.isnull().any())
# 第三步 筛选特征值和目标值
x = data.iloc[:, 1:-1] # 表示每一行数据都要, 从第一列到倒数第二列的column字段也要
y = data["Class"]
x_train, x_test, y_train, y_test = train_test_split(x, y)
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
| 检测是否还有缺失值(全为false表示没有缺失值)
Sample code number False
Clump Thickness False
Uniformity of Cell Size False
Uniformity of Cell Shape False
Marginal Adhesion False
Single Epithelial Cell Size False
Bare Nuclei False
Bland Chromatin False
Normal Nucleoli False
Mitoses False
Class False
|
训练
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| # 第四步: 开始特征工程
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 第五步, 预估器流程
estimator = LogisticRegression() # 默认参数
estimator.fit(x_train, y_train)
print("逻辑回归_权重系数为: ", estimator.coef_)
print("逻辑回归_偏置为:", estimator.intercept_)
# 第六步, 模型评估
y_predict = estimator.predict(x_test)
print("逻辑回归_预测结果", y_predict)
print("逻辑回归_预测结果对比:", y_test == y_predict)
score = estimator.score(x_test, y_test)
print("准确率为:", score)
# 2是良性的 4是恶性的
"""
但是实际上这个预测结果不是我们想要的, 以上只能说明预测的正确与否,
而事实上, 我们需要一种评估方式来显示我们对恶性breast的预测成功率, 也就是召回率
同时可以查看F1-score的稳健性
(召回率和精确率看笔记和截图)
所以下面换一种评估方法
"""
|
输出
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| 逻辑回归_权重系数为: [[1.20895973 0.34430535 0.93605533 0.50117234 0.22296947 1.22295345
0.81648447 0.64096012 0.71930684]]
逻辑回归_偏置为: [-0.9875554]
逻辑回归_预测结果 [2 4 2 2 4 4 2 2 4 2 2 2 4 4 4 2 2 4 4 4 4 2 4 4 4 2 2 4 2 2 4 2 4 4 4 2 4
2 2 2 2 4 4 2 4 2 2 2 2 4 2 2 2 4 4 2 4 2 2 2 2 2 2 4 4 4 2 2 2 2 2 4 2 2
2 2 4 2 2 2 2 2 2 2 2 4 2 2 4 2 2 2 4 2 4 2 2 2 2 2 2 2 2 2 4 4 2 2 4 4 2
2 2 4 2 4 2 2 4 4 2 2 2 2 4 2 2 2 4 2 2 2 2 2 4 2 4 2 4 2 2 4 2 2 2 4 4 4
2 2 2 2 4 4 2 2 2 2 2 2 2 4 2 2 2 2 2 2 2 4 2]
逻辑回归_预测结果对比: 541 True
288 True
395 True
409 True
568 True
...
442 True
51 False
370 True
304 True
363 True
Name: Class, Length: 171, dtype: bool
准确率为: 0.9766081871345029
|
查看精确率,召回率,F1-score
1
2
3
4
| Score = classification_report(y_test, y_predict, labels=[2, 4],
target_names=["良性", "恶性"])
print("查看精确率,召回率,F1-score\n", Score)
# support表示样本量
|
输出
1
2
3
4
5
6
7
8
9
| 查看精确率,召回率,F1-score
precision recall f1-score support
良性 0.98 0.98 0.98 114
恶性 0.96 0.96 0.96 57
accuracy 0.98 171
macro avg 0.97 0.97 0.97 171
weighted avg 0.98 0.98 0.98 171
|
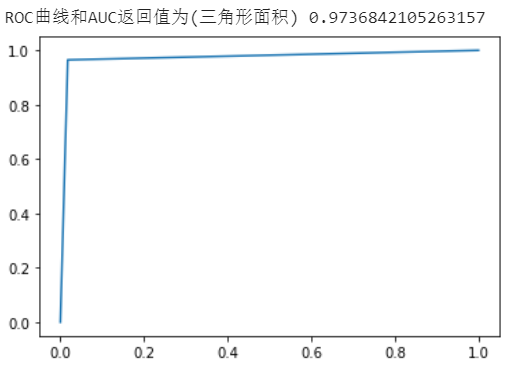
查看 ROC 曲线和 AUC 指标
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| """
ROC曲线和AUC指标(样本分类不均衡的情况下,可以使用这种方法)
AUC = 0.5 是瞎猜模型
AUC = 1 是最好的模型
AUC < 0.5 属于反向毒奶
更多的看截图
"""
# 需要转换为0,1表示
y_true = np.where(y_test > 3, 1, 0) # 表示大于3为1,反之为0(class值为2和4)
return_value = roc_auc_score(y_true, y_predict)
print("ROC曲线和AUC返回值为(三角形面积)", return_value)
fpr, tpr, thresholds = roc_curve(y_true, y_predict)
plt.plot(fpr, tpr)
plt.show()
|
输出
回归
(Regression)
- 小规模数据:
- LinearRegression(不能解决拟合问题)
- 岭回归
- 大规模数据:SGDRegressor
线性回归
1
| from sklearn.linear_model import LinearRegression, SGDRegressor
|
(Linear Regression)
线性回归 (Linear regression) 是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式
API
正规方程
正规方程的优化方法,不能解决拟合问题,一次性求解,针对小数据
- LinearRegression(fit_intercept=True)
- fit_intercept:是否计算偏置
- 属性
- LinearRegression.coef_:权重系数(回归系数)
- LinearRegression.intercept_:偏置
梯度下降
其实是随机梯度下降
- SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
- SGDRegressor 类实现了随机梯度下降学习,它支持不同的 loss 函数和正则化惩罚项来拟合线性回归模型。
- loss:损失类型
- loss=”squared_loss”: 普通最小二乘法
- fit_intercept:是否计算偏置
- learning_rate:string, optional
- 学习率填充,对于一个常数值的学习率来说,可以使用 learning_rate=’constant’ ,并使用 eta0 来指定学习率。
- ‘constant’:eta = eta0
- ‘optimal’:eta = 1.0 / (alpha * (t + t0)) [default]
- ‘invscaling’:eta = eta0 / pow(t, power_t=0.25)
- max_iter:迭代次数
- 属性
- SGDRegressor.coef_:回归系数
- SGDRegressor.intercept_:偏置
对比
| 梯度下降 | 正规方程 |
|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高 O(n3) |
回归性能评估
均方误差 MSE
1
| from sklearn.metrics import mean_squared_error
|
均方误差(Mean Squared Error)MSE 评价机制
mean_squared_error(y_test, y_pred)
- 均方误差回归损失
- y_test:真实值
- y_pred:预测值
- return:浮点数结果
平均绝对误差 MAE
1
| from sklearn.metrics import mean_absolute_error
|
mean_absolute_error(y_test, y_pred)
- 平均绝对误差回归损失
- y_test:真实值
- y_pred:预测值
- return:浮点数结果
例
初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error # 均方误差
boston_data = load_boston()
print("特征数量为:(样本数,特征数)", boston_data.data.shape)
x_train, x_test, y_train, y_test = train_test_split(boston_data.data,
boston_data.target, random_state=22)
# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
|
正规方程
1
2
3
4
5
6
7
8
9
10
| estimator = LinearRegression()
estimator.fit(x_train, y_train)
print("正规方程_权重系数为: ", estimator.coef_)
print("正规方程_偏置为:", estimator.intercept_)
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print("正规方程_房价预测:", y_predict)
print("正规方程_均分误差:", error)
|
输出
1
2
3
4
5
6
7
8
9
10
| 正规方程_权重系数为: [-0.64817766 1.14673408 -0.05949444 0.74216553 -1.95515269 2.70902585
-0.07737374 -3.29889391 2.50267196 -1.85679269 -1.75044624 0.87341624
-3.91336869]
正规方程_偏置为: 22.62137203166228
正规方程_房价预测: [28.22944896 31.5122308 21.11612841 32.6663189 20.0023467 19.07315705
21.09772798 19.61400153 19.61907059 32.87611987 20.97911561 27.52898011
15.54701758 19.78630176 ......
15.17700342 3.81620663 29.18194848 20.68544417 22.32934783 28.01568563
28.58237108]
正规方程_均分误差: 20.627513763095386
|
梯度下降
1
2
3
4
5
6
7
8
9
10
11
| estimator = SGDRegressor(learning_rate="constant", eta0=0.01, max_iter=10000)
# estimator = SGDRegressor(penalty='l2', loss="squared_loss") # 这样设置就相当于岭回归, 但是建议用Ridge方法
estimator.fit(x_train, y_train)
print("梯度下降_权重系数为: ", estimator.coef_)
print("梯度下降_偏置为:", estimator.intercept_)
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print("梯度下降_房价预测:", y_predict)
print("梯度下降_均分误差:", error)
|
输出
1
2
3
4
5
6
7
8
9
| 梯度下降_权重系数为: [-0.63057536 1.10395195 0.0426204 1.11219718 -1.91486635 2.72806163
-0.05021542 -3.52443232 2.47863671 -1.62374879 -1.9093765 1.08972091
-4.48569927]
梯度下降_偏置为: [22.36660176]
梯度下降_房价预测: [28.44139247 31.71808756 20.86031611 34.1638423 19.35660167 19.18397968
20.97064914 18.87641833 18.87914517 ......
14.57654182 2.54082058 29.38973401 20.80732646 21.65598607 27.85659704
29.41864109]
梯度下降_均分误差: 20.997365545229272
|
岭回归
(Ridge Regression)
1
| from sklearn.linear_model import Ridge, RidgeCV
|
岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上正则化的限制,从而达到解决过拟合的效果
原理
正则化类别
- L2 正则化
- 作用:可以使得其中一些 W 的都很小,都接近于 0,削弱某个特征的影响
- 优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象
- Ridge 回归
- L1 正则化
- 作用:可以使得其中一些 W 的值直接为 0,删除这个特征的影响
- LASSO 回归
线性回归的损失函数用最小二乘法,等价于当预测值与真实值的误差满足正态分布时的极大似然估计;岭回归的损失函数,是最小二乘法+L2范数,等价于当预测值与真实值的误差满足正态分布,且权重值也满足正态分布(先验分布)时的最大后验估计;LASSO的损失函数,是最小二乘法+L1范数,等价于等价于当预测值与真实值的误差满足正态分布,且且权重值满足拉普拉斯分布(先验分布)时的最大后验估计
API
常规岭回归
Ridge(alpha=1.0, fit_intercept=True,solver=“auto”, normalize=False)
具有 L2 正则化的线性回归
alpha:正则化力度,也叫 λ,即惩罚项系数
solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
normalize:数据是否进行标准化
normalize=False:可以在 fit 之前调用 preprocessing.StandardScaler 标准化数据
属性
Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
Ridge 方法相当于 SGDRegressor(penalty='l2', loss="squared_loss"), 只不过 SGDRegressor 实现了一个普通的随机梯度下降学习,推荐使用 Ridge(实现了 SAG)
交叉验证岭回归
RidgeCV(_BaseRidgeCV, RegressorMixin)
- 具有 L2 正则化的线性回归,可以进行交叉验证
- alphas:alpha 列表
- cv:交叉验证次数
- coef_:回归系数
例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| from sklearn.linear_model import Ridge, RidgeCV
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error # 均方误差
boston_data = load_boston()
x_train, x_test, y_train, y_test = train_test_split(boston_data.data,
boston_data.target, random_state=22)
# 标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 岭回归
estimator = Ridge(max_iter=10000, alpha=0.5) # 岭回归
# estimator = RidgeCV(alphas=[0.1, 0.2, 0.3, 0.5]) # 加了交叉验证的岭回归
estimator.fit(x_train, y_train)
print("岭回归_权重系数为: ", estimator.coef_)
print("岭回归_偏置为:", estimator.intercept_)
y_predict = estimator.predict(x_test)
error = mean_squared_error(y_test, y_predict)
print("岭回归_房价预测:", y_predict)
print("岭回归_均分误差:", error)
|
输出
1
2
3
4
5
6
7
8
| 岭回归_权重系数为: [-0.64193209 1.13369189 -0.07675643 0.74427624 -1.93681163 2.71424838
-0.08171268 -3.27871121 2.45697934 -1.81200596 -1.74659067 0.87272606
-3.90544403]
岭回归_偏置为: 22.62137203166228
岭回归_房价预测: [28.22536271 31.50554479 21.13191715 32.65799504 20.02127243 19.07245621
21.10832868 19.61646071 ......15.19441045 3.81755887 29.1743764 20.68219692 22.33163756 28.01411044
28.55668351]
岭回归_均分误差: 20.641771606180914
|
聚类
1
| from sklearn.cluster import KMeans
|
K-means(K 均值聚类)
- 特点:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类)
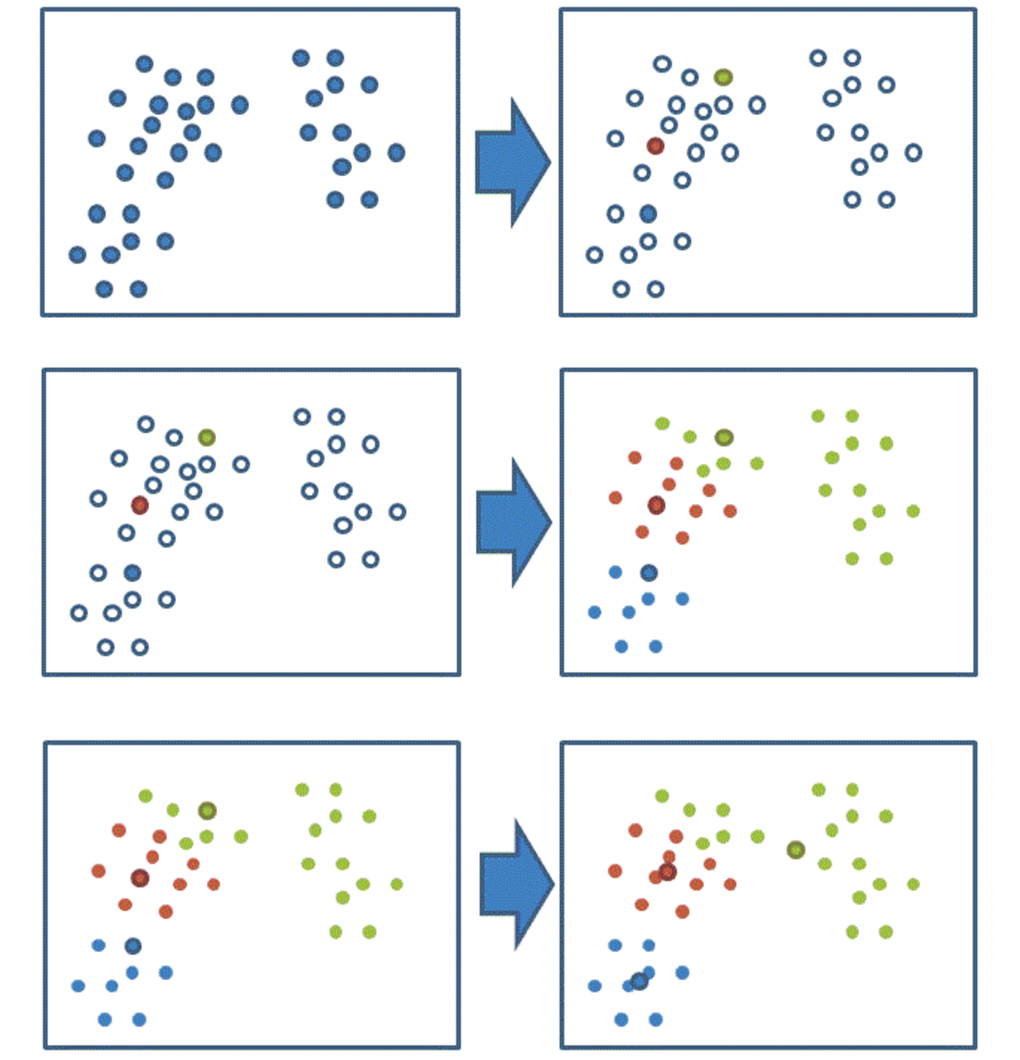
聚类步骤
随机设置 K 个特征空间内的点作为初始的聚类中心
对于其他每个点计算到 K 个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程
API
KMeans(n_clusters=8, init=‘k-means++’…)
- n_clusters:开始的聚类中心数量
- init:初始化方法,默认为’k-means ++’
KMeans.labels_:默认标记的类型,可以和真实值比较(不是值比较)
轮廓系数
1
| from sklearn.metrics import silhouette_score
|
轮廓系数作为 Kmeans 的性能评估指标
公式
$$
sc_i=\cfrac{b_i-a_i}{max(b_i,a_i)}
$$
注:对于每个点 $i$ 为已聚类数据中的样本 ,$b_i$ 为 $i$ 到其它族群的所有样本的距离最小值,$a_i$ 为 $i$ 到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值
轮廓系数值分析
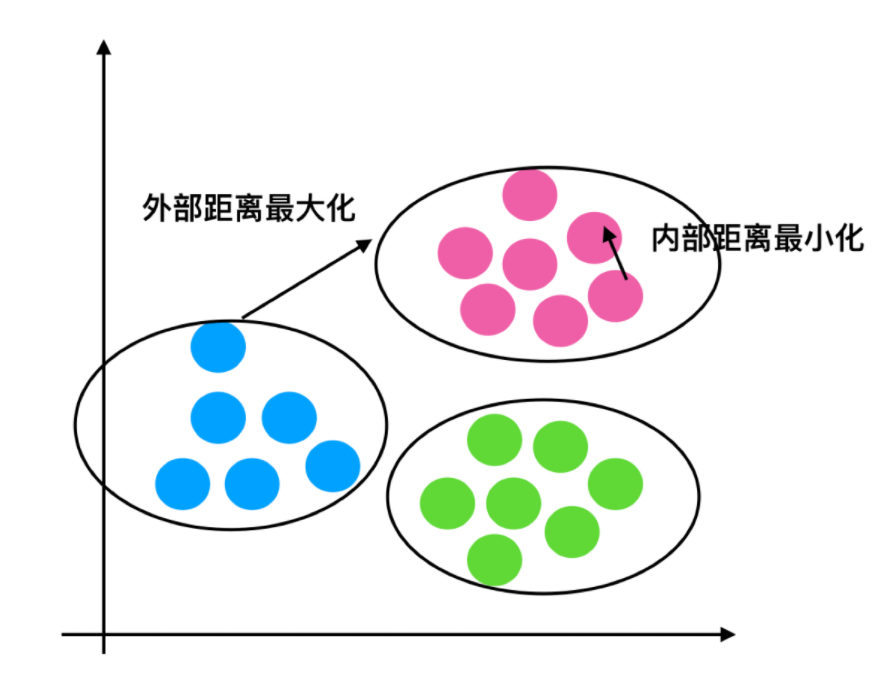
分析过程(以一个蓝 1 点为例)
计算出蓝 1 离本身族群所有点的距离的平均值$a_i$
蓝 1 到其它两个族群的距离计算出平均值红平均,绿平均,取最小的那个距离作为$b_i$
根据公式:极端值考虑:如果$b_i »a_i$,那么公式结果趋近于 1;如果$a_i»>b_i$,那么公式结果趋近于-1
结论:如果$b_i»a_i$,趋近于 1,效果好, $b_i«a_i$,趋近于-1,效果不好。轮廓系数的值是介于 [-1,1] ,越趋近于 1 代表内聚度和分离度都相对较优
API
- silhouette_score(X, labels):计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值(聚类结果)
例
分析
降维之后的数据
k-means 聚类
聚类结果显示
用户聚类结果评估
1
2
3
4
5
6
7
8
| import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets.samples_generator import make_blobs
# X为样本特征,Y为样本簇类别, 共1000个样本,每个样本2个特征,共4个簇,簇中心在[-1,-1], [0,0],[1,1], [2,2], 簇方差分别为[0.4, 0.2, 0.2]
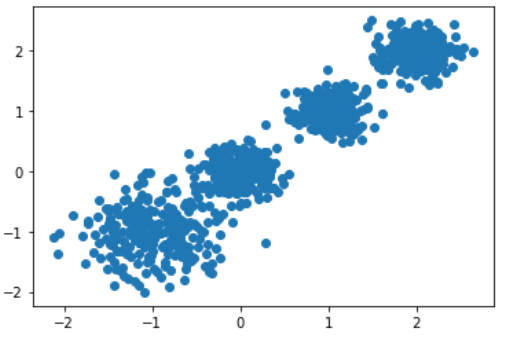
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.2, 0.2, 0.2])
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
|
案例样本
1
2
3
4
5
6
7
8
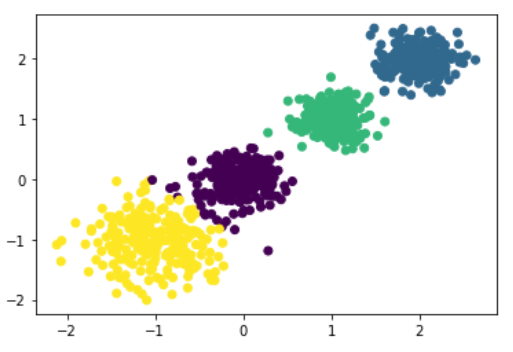
9
| from sklearn.cluster import KMeans
#y_pred = KMeans(n_clusters=4).fit_predict(X)
estimator = KMeans(n_clusters=4, init='k-means++')
estimator.fit(X)
y_pred = estimator.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
|
1
2
3
4
| from sklearn.metrics import silhouette_score
score = silhouette_score(X, y_pred)
print("模型轮廓系数为(1 最好, -1 最差):", score)
|
输出
1
| 模型轮廓系数为(1 最好, -1 最差): 0.6634549555891298
|










