数字图像整理
数字图像处理
数字图像基础
图像取样和量化
概念
一幅图像的 x 和 y 坐标及幅度可能都是连续的。为将它转换为数字形式,必须对坐标和幅度都进行取样操作。
对坐标值进行数字化称为取样
对幅值(灰度值)数字化称为量化
数字图像表示
令 f(s, t) 表示一幅具有两个连续变量 s 和 t 的连续图像函数。
通过取样和量化,可以把该函数转换为数字图像。
假设把这幅连续图像取样为一个二维阵列 f(x, y) ,其中 (x, y) 是离散坐标。
通常,图像在任何坐标 (x, y) 处的值记为 f(x, y),其中 x 和 y 都是整数。
由一幅图像的坐标张成的实平面部分称为空间域,x 和 y 称为空间变量或空间坐标。
f(x, y) 的表示方法
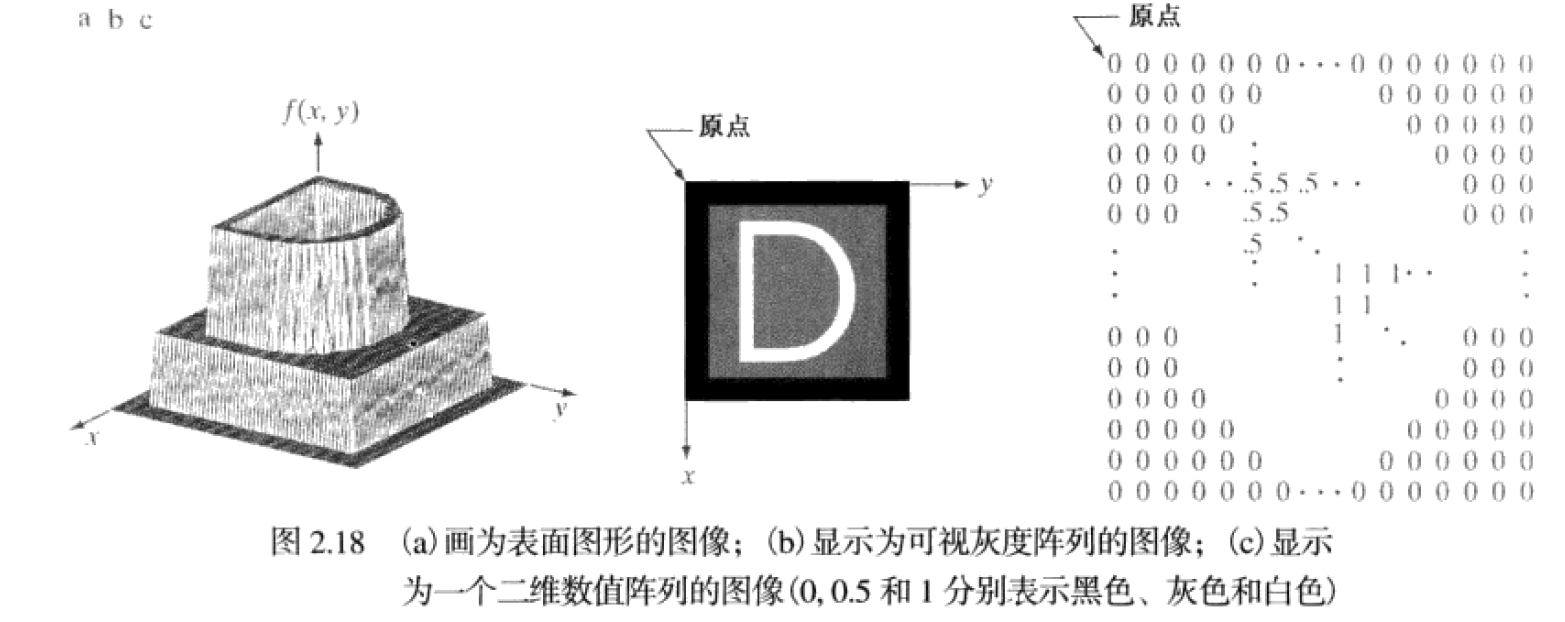
图像显示(如图 b)允许我们快速地观察结果。数值阵列(如图 c)用于处理和算法开发
数字图像的原点位于左上角,其中正 x 轴向下延伸,正 y 轴向右延申
一些规定
M 和 N(行和列)规定为整数
灰度级数通常取为 2 的整数次幂
$$ L=2^k $$
多数情形下,灰度值都会被缩放到用于图像存储和显示的整数区间 [0, L-1]
动态范围
灰度跨越的值域被称为动态范围(这里,将图像系统的动态范围定义为系统中最大可度量灰度与最小可检测灰度之比)
动态范围上限取决于饱和度,下限取决于噪声。基本上,动态范围由系统能表示的最低和最高灰度级来确定
将一幅图像中最高和最低灰度级间的灰度差定义为对比度。当一幅图像中像素可感知的数值具有高动态范围时,那么我们认为该图像具有高对比度。
存储数字图像所需的比特数 b 为 $$ b=M\times N\times k $$
当一幅图像有 2^k^ 个灰度级时,实际上通常称该图像为一幅 “k 比特图像”。例如,有 256 个可能的离散灰度值的图像称为 8 比特图像
空间分辨率
空间分辨率是图像中可辩别的最小细节的度量。在数量上,空间分辨率可以有很多方法来说明,其中单位距离的线对数和单位距离的点数(像素数) 是最通用的度量
灰度分辨率
类似地,灰度分辨率是指在灰度级中可分辨的最小变化,是主观指标
数字图像的平滑区域中的灰度级数不足引起的轮廓形状常称为伪轮廓
伪轮廓通常在以 16 或更少级数均匀设置的灰度级显示的图像中十分明显。
例如:当原图的灰度级是 256 时,两个位置的像素值只差 1 , 则在图像显示上不会有太大的差异,依旧观察不出来;但是当灰度级变为 8 时,两个位置的像素值相差 1 ,则会有明显的差异,因此也就产生了伪轮廓
放大和收缩数字图像
采用复制行/列可以实现整数倍的放大图像,采用删除行/列可以实现整数倍的缩小图像,但两种方法都无法实现任意倍数和任意位置的放大和缩小图像
步骤
- 计算新的像素在原图的对应位置;
- 为这些对应位置赋灰度值。
计算新像素在原图的对应位置
f(x,y) 表示输出图像,g(u,v) 表示输入图像。几何运算(图像的放大或缩小也是图像的几何运算)可定义为:
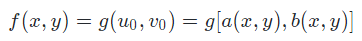
- 如果令:$u_0 = a(x,y) = x$; $v_0 = b(x,y) = y$
- 那么仅仅是把 g 拷贝到 f 而不加任何改动的恒等运算。
- 如果令:$u_0 = a(x,y) = x + x_0$; $v_0 = b(x,y) = y + y_0$
- 那么得到平移运算,其中点 (x~0~,y~0~) 被平移到原点
- 如果令:$u_0 = a(x,y) = x/c$; $v_0 = b(x,y) = y/d$
- 那么会使图像在 x 轴方向放大 c 倍,在 y 轴放大 d 倍。
- 例如:将一幅 200x200 的图像 g(u,v) 放大 1.5 倍,那么将得到 300x300 的新图像 f(x,y)。
- 产生新图像的过程,实际就是为 300x300 的像素赋值的过程。
- 假如为 f(150,150) 赋值 $f(150,150) = g(150/1.5,150/1.5) = g(100,100)$;
- 假如为 f(100,100) 赋值 $f(100,100) = g(100/1.5,100/1.5) = g(66.7,66.7)$
- 由于图像像素都是在整数坐标中,所以没有坐标值为 (66.7,66.7) 的像素。所以要采用插值的方法给其赋值。
为这些对应位置赋灰度值
因为 (u~0~, v~0~) 不一定要在坐标点上,故需要插值求 g(u~0~, v~0~);
- 最近邻内插
- 取点 (u~0~, v~0~) 最近的整数坐标 (u, v)。在上述例子中,为了求 (66.7, 66.7) 的灰度值,则用 (67, 67) 的灰度值来做插值
- 双线性插值
- 根据四个邻点的灰度值通过插值计算 g(u~0~, v~0~)
- 更多邻点的内插
- 更高次内插,这种方法往往能取得更为精确的结果,但是相应的计算量也会更大)
图像内插
我他妈也不知道到底考不考
像素间的一些基本关系
相邻像素
p 的水平垂直相邻像素,称为 p 的 4 邻域,记为 N~4~(p) p 的 4 个对角邻像素,称为 p 的 D 邻域,记为 N~D~(p) 4 邻域和 D 邻域合在一起称为 p 的 8 邻域,记为 N~8~(p)
邻接性
令 V 是用于定义邻接性的灰度值集合,V 中可能定义了很多灰度值,例如,在灰度值范围为 0 到 255 的邻接像素中,集合 V 可能是这 256 个值的任何一个子集。考虑三种类型的邻接:
4 邻接:如果 q 在 N~4~(p) 集中,具有 V 中数值的两个像素 p 和 q 是 4 邻接的
8 邻接:如果 q 在 N~8~(p) 集中,具有 V 中数值的两个像素 p 和 q 是 8 邻接的
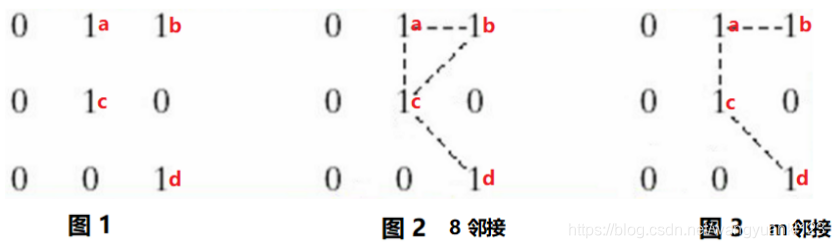
m 邻接(混合邻接):有两种情况
- q 在 N~4~(p) 中,
- q 在 N~D~(p) 中且集合 N~4~(p) ∩ N~4~(q) 中没有 V 值的像素,
混合邻接是 8 邻接的改进。混合邻接的引入是为了消除 8 邻接常常发生的二义性。
连通性
通路
从具有坐标 (x, y) 的像素 p 到具有坐标 (s, t) 的像素 q 的 通路(或曲线) 是特定的像素序列,通路上任意相邻的两个像素点满足某种邻接性
连通、连通分量和连通集
令 S 是图像中的一个像素子集。如果在 S 中,p 和 q 之间存在一个全部由 S 中的元素组成的通路
- 则可以说两个像素 p 和 q 在 S 中是连通的
- 对于 S 中的任何像素 p,S 中连通到该像素的像素集叫做 S 的连通分量
- 如果 S 仅有一个连通分量,则集合 S 叫做连通集
区域
令 R 是图像中的一个像素子集。
- 如果 R 是连通集,则称 R 为一个区域
- 两个区域,如果它们联合形成一个连通集,则区域 Ri 和 Rj 称为邻接区域,不邻接的区域称为 不连接区域
- 一个区域 R 的边界(也称为边缘或轮廓)是区域中像素的集合,该区域有一个或多个不在 R 中的邻点
前景和背景
假设一幅图像包含有 K 个不连接的区域,即 R~k~,k = 1, 2, ··· , K ,且它们都不接触图像的边界。令 R~u~ 代表所有 K 个区域的并集,并且令 (R~u~)^c^ 代表其补集(集合 S 的补集是不在 S 中的点的集合)。我们称 R~u~ 中的所有点为图像的前景,而称 (R~u~)^c^ 中的所有点为图像的背景
距离
欧几里得(欧式)距离
p 和 q 间的欧几里得(欧式)距离定义如下:
$$ D_e(p,q)=[(x−s)^2+(y−t)^2]^{\frac{1}{2}} $$
对于距离度量,距点 (x, y) 的距离 D~e~ 小于等于某个值 r 的像素,是中心在 (x, y) 且半径为 r 的圆平面
D~4~ 距离
又叫城市街区距离(曼哈顿距离)
p 和 q 间的 D~4~ 距离定义如下: $$ D_4(p,q)=|x-s|+|y-t| $$ 此情况下,距 (x, y) 的距离 D~4~ 小于等于某个值 r 的像素形成一个中心在 (x, y) 的菱形。
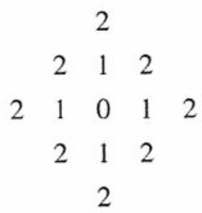
其中 D~4~ = 1 的像素是 (x, y) 的 4 邻域。
D~8~ 距离
又叫棋盘距离(切比雪夫距离)
p 和 q 间的 D~8~ 距离定义如下: $$ D_8(p,q)=max(|x-s|,|y-t|) $$ 此情况下,距 (x, y) 的 D8 距离小于等于某个值 r 的像素形成中心在 (x, y) 的 方形

其中 D~8~ = 1 的像素是 (x, y) 的 8 邻域。
D~m~ 距离
p 和 q 间的距离 D~m~ 定义为最短 m 通路的长度
注意,p 和 q 之间的 D~4~ 距离和 D~8~ 距离与任何通路无关。
例题
如下图所示,对于 V={1},求像素点 p 和像素点 q 的城市街区距离、棋盘距离和 D~m~ 距离
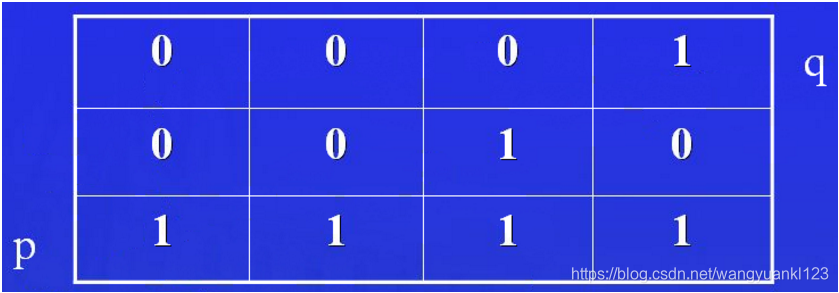
由于 D~4~ 距离和 D~8~ 距离与任何通路无关,所以:
$$
D_4(p, q) = |x - s| + |y - t| = 2 + 3 = 5 \
D_8(p, q) = max(|x - s|, |y - t|) = max(2, 3) = 3
$$
求 D~m~ 距离首先要找到像素点 p 和像素点 q 之间的一条 m 通路,如图中虚线所示:
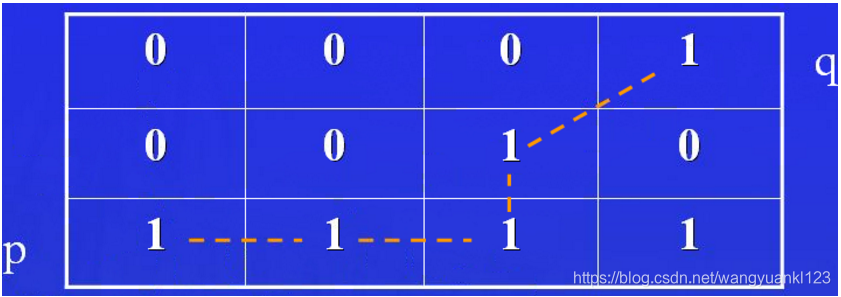
故 D~m~(p, q) = 4
灰度变换与空间滤波
术语空间域指图像平面本身,这类图像处理方法直接操作图像中的像素。
变换域的图像处理首先把一幅图像变换到变换域,在变换域中进行处理,然后通过反变换把处理结果返回到空间域。
空间域处理主要分为灰度变换和空间滤波两类。
灰度变换对图像的单个像素进行操作,主要以对比度和阈值处理为目的。
空间滤波涉及改善性能的操作,如通过图像中每个像素的邻域处理来锐化图像
背景知识
空间域是包含图像像素的简单平面。空间域技术直接操作图像的像素。
例如,频率域的操作在图像的傅里叶变换上执行,而不是在图像本身上执行。
通常,空间域技术在计算上更有效,且执行所需的处理资源较少。
空间域处理 可由下式表示: $$ g(x, y) = T[f(x,y)] $$ 式中,f(x, y) 是输入图像,g(x, y) 是处理后的图像,T 是在点 (x, y) 的邻域上定义的关于 f 的一种算子。
算子可以应用于单幅图像或图像集合。邻域一般选择矩形邻域,这样更方便计算机实现。
空间滤波
- 邻域原点从一个像素向另一个像素移动,对邻域中的像素应用算子 T ,并在该位置产生输出。
- 这样,对于任意指定的位置 (x, y) :图像 g 在这些坐标处的值,等于对 f 中以 (x, y) 为原点的邻域应用算子 T 的结果。
- 例如,假如该邻域是大小为 3 × 3 的正方形,算子 T 定义为 “计算该邻域的平均灰度”。
- 考虑图像中的任意位置,譬如 (100, 150)。
- 假设该邻域的原点位于其中心处,则在该位置的结果 g(100, 150) 是计算 f(100, 150) 和其 8 个邻点的和,再除以 9(即由邻域包围的像素灰度的平均值)
- 然后,邻域原点移到下一个位置,并重复前面的过程,产生下一个输出图像 g 的值。
- 该处理通常从输入图像的左上角开始,以水平扫描的方式逐像素地处理,每次一行。
- 当该邻域的原点位于图像的边界上时,部分邻域将位于图像的外部。
- 此时,一种方法是用 T 做指定的计算时忽略外侧邻点
- 或者用 0 或其他指定的灰度值填充图像的边缘。
- 被填充边界的厚度取决于邻域的大小。
以上过程称为空间滤波,其中邻域与预定义的操作一起称为空间滤波器(也成为空间掩膜、核、模板或窗口)
最小邻域的大小为 1 × 1
在这种情况下,g 仅取决于点 (x, y) 处的 f 值,而 T 则成为一个形如下式的灰度 (也称为灰度级或映射或强度映射) 变换函数: $$ s = T(r) $$ 式中,令 r 和 s 分别表示变量,即 g 和 f 在任意点 (x, y) 处的灰度
T(r) 有多种形式:
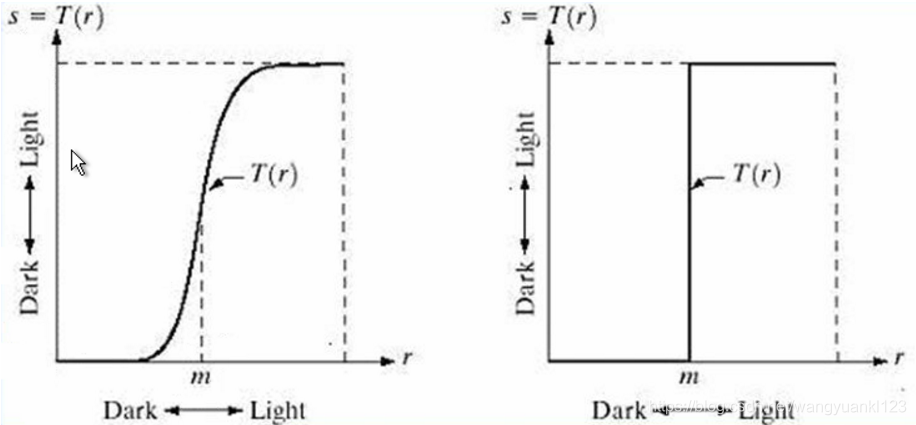
左图中,这种变换将会产生比原始图像更高的对比度(灰度级低于 m 时变暗,而灰度级在 m 以上时变亮),这种技术有时称为对比度拉伸。
在极限情况下,如右图所示,T( r ) 产生了一幅两级(二值)图像。这种形式的映射称为阈值处理函数。
结果仅取决于一个点的灰度的方法,有时称为点处理技术,与之相对的有邻域处理技术。
一些基本的灰度变换函数
灰度变换是所有图像处理技术中最简单的技术,是一种点处理技术
由于处理的是数字量,变换函数的值通常存储在一个一维阵列中,并且从 r 到 s 的映射通过查表得到。对于 8 比特环境,一个包含 T 值的可查阅的表需要有 256 个记录
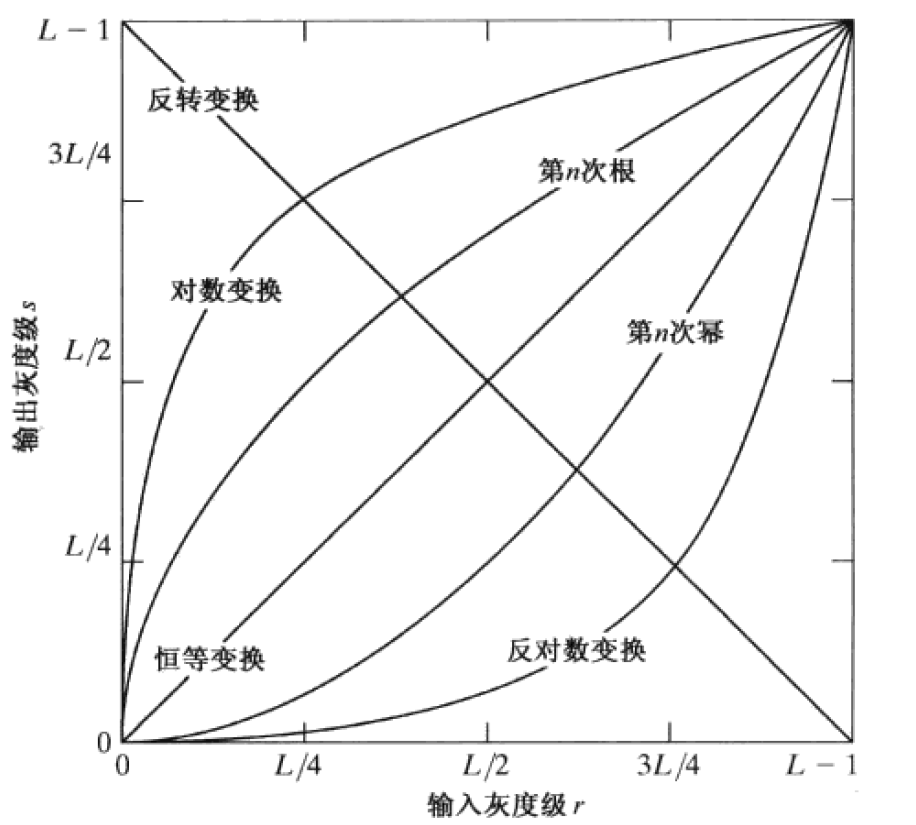
如上图显示了图像增强常用的三类基本函数:线性函数(反转和恒等变换)、对数函数(对数和反对数变换)和幂律函数(n 次幂和 n 次根变换)。
图像反转
对于灰度级范围为 [0, L-1] 的一幅图像,该图像的反转由下式给出: $$ s=L-1-r $$ 使用这种方式反转一幅图像的灰度级,可得到等效的照片底片。这种类型的处理特别适用于增强嵌入图像暗色区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时。
对数变换
$$ s=c\times log(1+r) $$
式中 c 是常数,并假设 r>=0
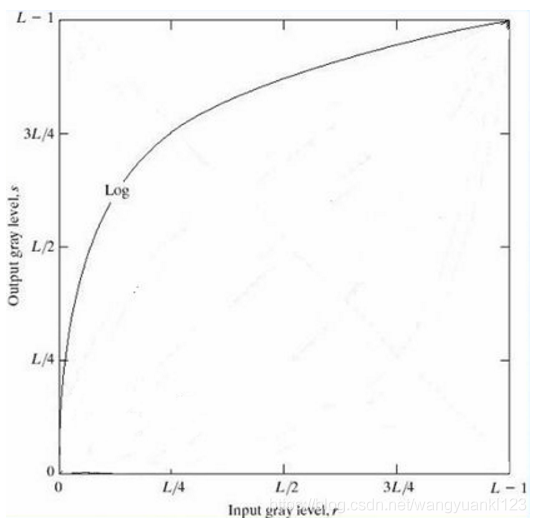
此变换将输入中范围较窄的低灰度值映射为输出中范围较宽的灰度值,或将输入中范围较宽的高灰度值映射为输出中范围较窄的灰度值。
使用这种类型的变换来扩展图像中的暗像素值,同时压缩更高灰度级的值。反对数变换的作用与此相反。
对数函数压缩像素值变化较大的图像的动态范围,如傅里叶频谱

幂律(伽马)变换
$$ s=cr^\gamma $$
其中 c 和 γ 为正常数。对于不同的 γ 值,s 与 r 的关系曲线如下图所示。与对数变换情况类似,部分 γ 值的幂律曲线将较窄范围的暗色输入值映射为较宽范围的输出值,或将较宽范围的高灰度级输入值映射为较窄范围的输出值。