计组 第二章
运算方法和运算器
定点加法、减法运算
补码加法
[x+y]补=[x]补+[y]补
符号位运算丢进位

补码减法
减法变成加法来做
-y 的补码 = y 的补码所有位取反 +1
[x]补 - [y]补 = [x]补 + [-y]补
[-y]补 = -[y]补 + 2^-n^ (弱智方法,直接求 -y 的补码即可)

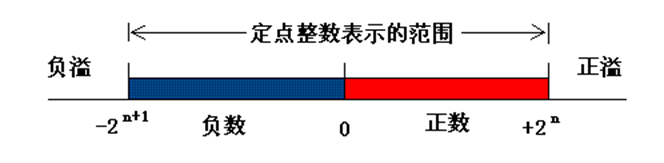
溢出
概念
可能产生溢出的情况
两正数加,变负数,正溢(大于机器所能表示的最大数)
两负数加,变正数,负溢(小于机器所能表示的最小数)


检测方法
双符号位法(变形补码)
00 为正,11 为负,有下表
| $S_{f1}$ | $S_{f2}$ | 判断 |
|---|---|---|
| 0 | 0 | 正数 |
| 0 | 1 | 正溢 |
| 1 | 0 | 负溢 |
| 1 | 1 | 负数 |
$S_{f1},S_{f2}$为结果的双符号,关系为异或

- 单符号位法
| $C_f$ | $C_0$ | 判断 |
|---|---|---|
| 0 | 0 | 正数 |
| 0 | 1 | 正溢 |
| 1 | 0 | 负溢 |
| 1 | 1 | 负数 |
其中$C_f$为符号位产生的进位,$C_0$为最高有效位产生的进位
定点乘法、除法运算
原码并行乘法
一般都用原码算
用绝对值算,且计算时不带符号位
原码阵列,结果是原码;补码阵列,结果变为补码
不带符号位的阵列乘法器
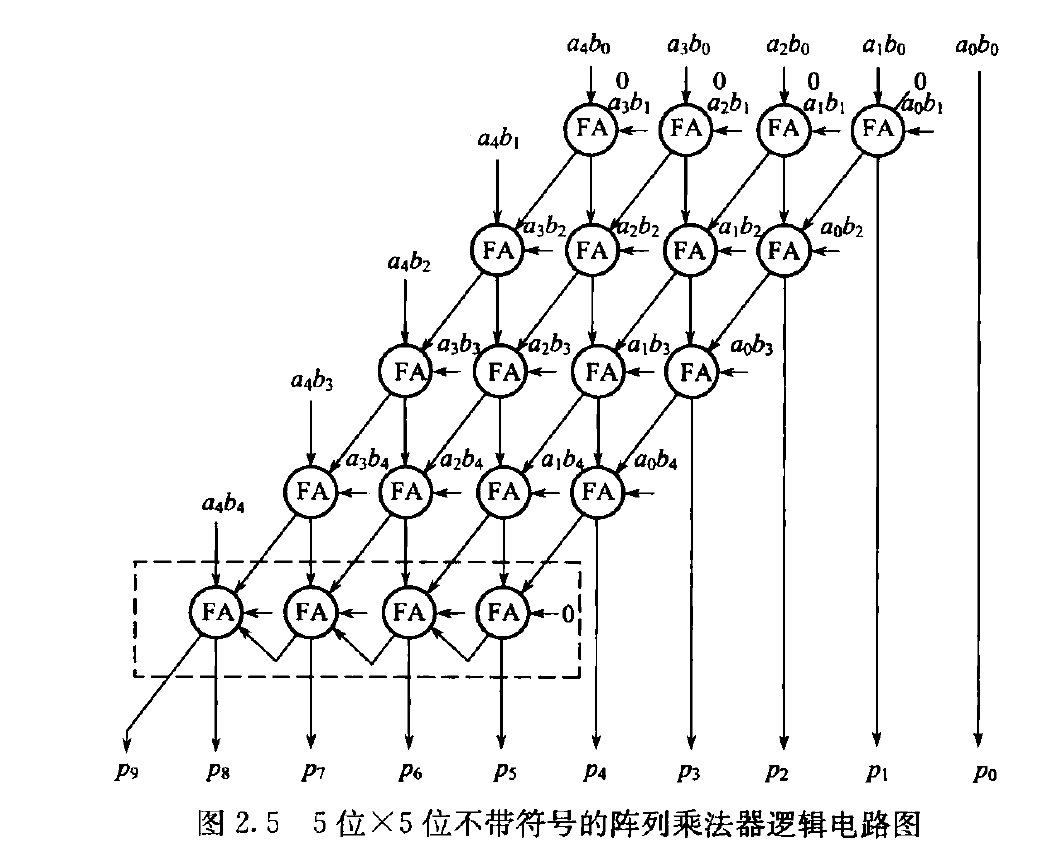

带符号的阵列乘法器


定点除法
一般都用补码算
人工除法时,人可以比较被除数(余数)和除数的大小来确定商 1(够减)或商 0(不够减)
机器除法时,余数为正表示够减,余数为负表示不够减。不够减时必须恢复原来余数,才能继续向下运算。这种方法叫恢复余数法,控制比较复杂。
不恢复余数法(加减交替法)
- 余数为正,商 1,下次除数右移做减法;
- 余数为负,商 0,下次除数右移做加法。
- 控制简单,有规律
手工方案

不恢复余数法


浮点加法,减法运算
运算步骤
- 0 操作数检查;
- 比较阶码并完成对阶(小阶向大阶对齐);
- 尾数加减运算;
- 结果规格化;(尾数右移一位,阶码加一)
- 舍入处理
要点
用补码表示阶码和尾数
加减后溢出不是真正的溢出,规格化后才是真正的溢出
例


舍入处理(对阶和向右规格化时)
- 就近舍入(0 舍 1 入):类似”四舍五入”,丢弃的最高位为 1,进 1
- 朝 0 舍入:截尾
- 朝$+\infty$舍入:正数多余位不全为”0”,进 1;负数,截尾
- 朝$-\infty$舍入:负数多余位不全为”0”,进 1;正数,截尾
溢出判断和处理
- 阶码上溢,一般将其认为是$+\infty$和$-\infty$ 。
- 阶码下溢,则数值为 0
浮点乘法,除法运算
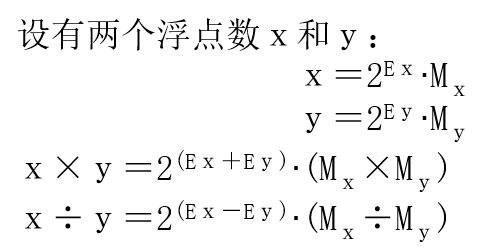
运算步骤
- 操作数检查
- 阶码加减操作
- 尾数乘除操作
- 结果规格化和舍入处理
IEEE754 标准
以 32 位为例
 $$
x=(-1)^S\times(1.M)\times2^{E-127}
$$
$$
x=(-1)^S\times(1.M)\times2^{E-127}
$$基数 R=2,基数固定,采用隐含方式来表示它。
S:数的符号位,1 位,在最高位,“0”表示正数,“1”表示负数。
M:尾数, 23 位,在低位部分,采用纯小数表示。
E:是阶码,8 位,采用移码表示。移码比较大小方便。
尾数域最左位(最高有效位)总是 1, 故这一位经常不予存储,而认为隐藏在小数点的左边。
采用这种方式时,将浮点数的指数真值 e 变成阶码 E 时,应将指数 e 加上一个固定的偏移值 127(01111111),即 ==E=e+127==。


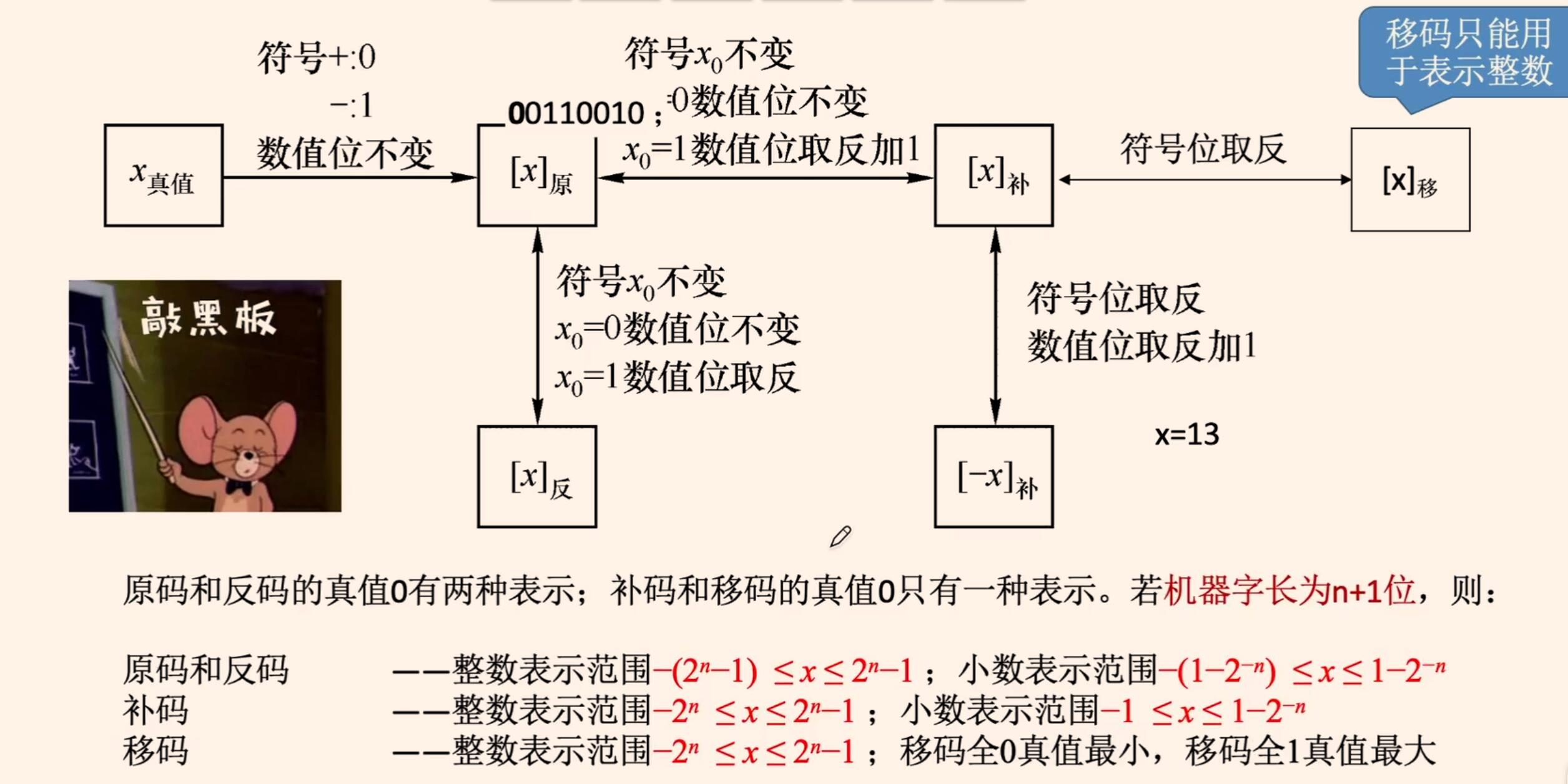
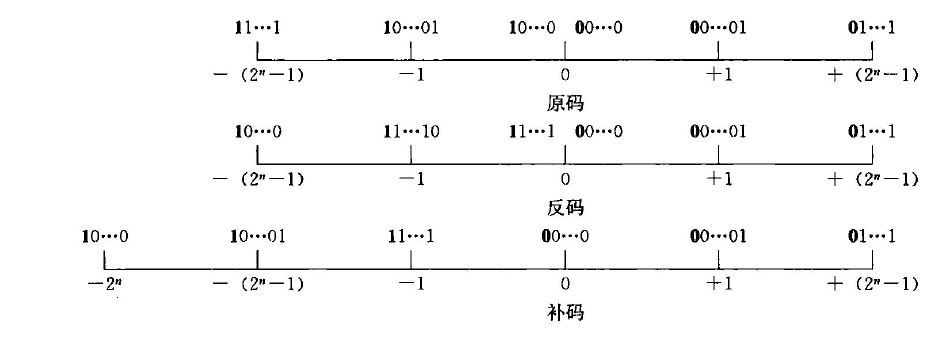
机器码

总线
机器内部各部份数据传送频繁,可以把寄存器间的数据传送通路加以归并,组成总线结构。
总线分类
- 所处位置
- 内部总线(CPU 内)
- 外部总线(系统总线)
- 逻辑结构
- 单向传送总线
- 双向传送总线
定点运算器的组成
单总线结构的运算器
在同一时间只能有一个操作数在总线上
操作速度慢
控制电路简单
双总线结构的运算器
- 不能直接把输出加到总线
三总线结构的运算器
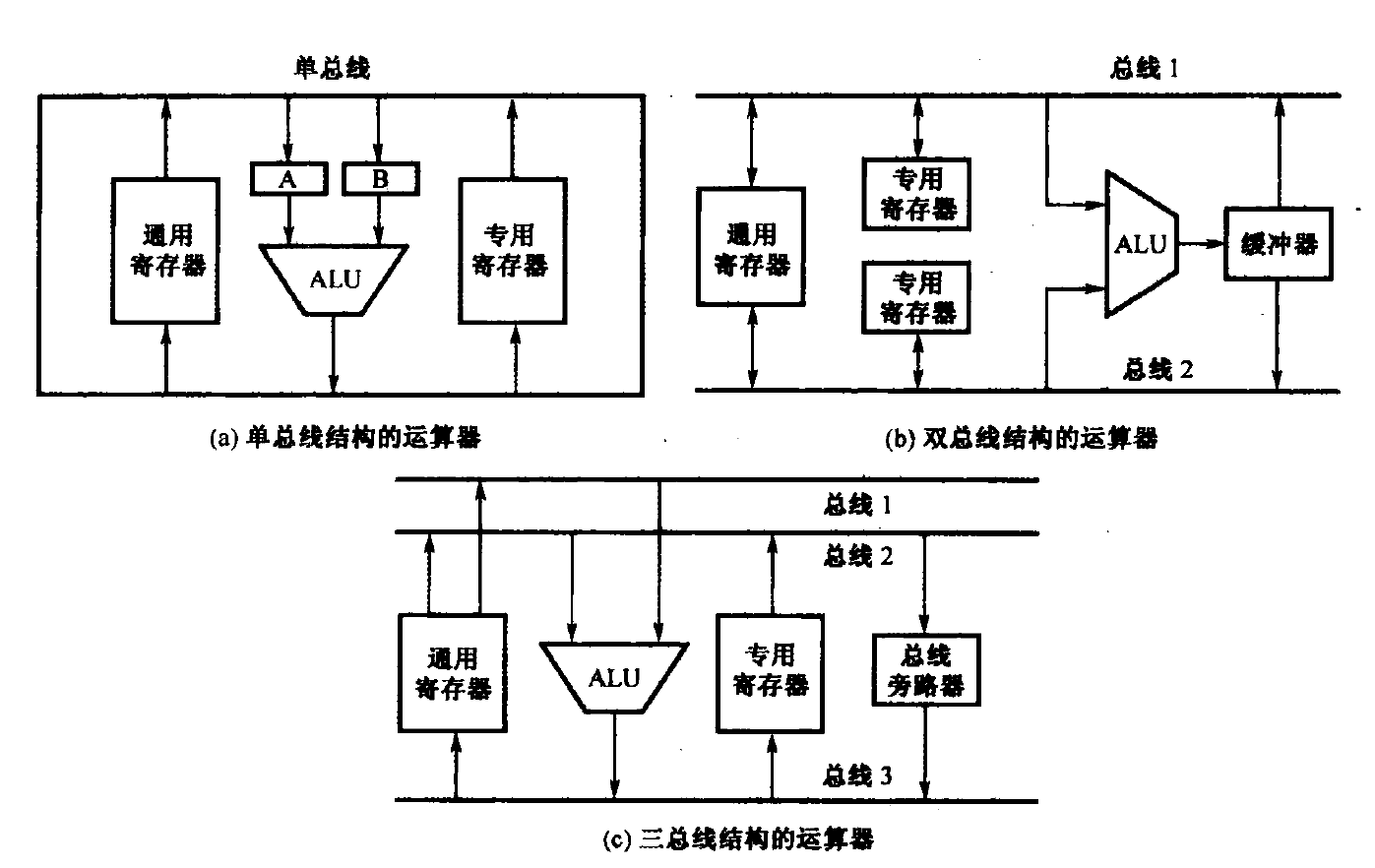
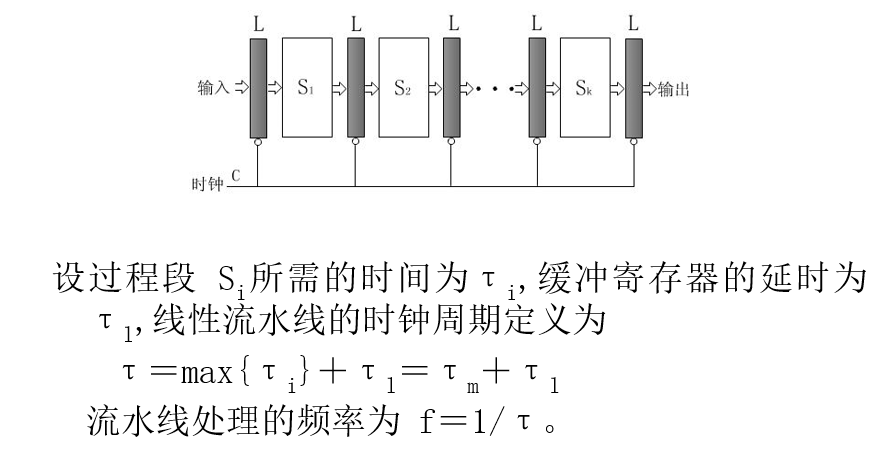
流水线
原理