伤心肠粉
伤心肠粉

离散数学2

MelonCholi 收录于  专业课
    约 3361 字   预计阅读 7 分钟 
目录

离散数学二

捋一捋

图论 50 分；代数系统 50 分

选择不定项

选择判断填空各 2 分，共 30 分，七道大题

图

4 道大题

基本概念

  • 概念为多，知道即可

  • 握手定理必考，特别是在涉及到度数时

  • 重点：简单图、完全图

连通性

  • 割集割点等，简单考判断，复杂考找

矩阵表示

  • 书例 6.10 考计算题，求通路数、回路数、邻接矩阵

特殊的图

  • 哈密顿图的两个充分条件用处不大，找哈密顿回路即可

  • 判断是否是欧拉图 / 哈密顿图（找回路就完事），找欧拉回路、哈密顿回路或说明理由。第二道大题

平面图

  • 两道大题会涉及，一个计算一个证明
  • 会计算顶点数、边数、面数；要用到握手定理、面次和公式、欧拉公式
  • 小题：判断是不是平面图；大题：证明不是平面图 (?)
  • P160 例 6.18

树

是图知识的应用

定理小看一哈

代数系统

二元运算

  • 第一个大题：证明交换、结合、幂等；求单位元、零元、可逆元；判断系统是半群、群还是独异点

群

  • 第二个大题：同态，证明子群

  • 大题：循环群的生成元、子群、子群格

  • 置换群的乘法、逆：考填空

图

图论是解决现实世界离散客体之间的关系的有力工具

基本概念

无向图与有向图

无序对与多重集合

无序对: 2 个元素构成的集合, 记作 (a,b)

无序积: $A & B={(x,y) | x\in A\land y\in B}$

image-20210402145634889

多重集合: 元素可以重复出现的集合。

重复度: 元素在多重集合中出现的次数

image-20210402145652444
无向图

$G=<V, E>$

  • 其中 $V\neq \empty$ 称为顶点集，其元素称为顶点或结点;

  • E 是 V&V 的多重子集，称为边集，其元素称为无向边，简称边。

  • 有时用 V(G) 和 E(G) 分别表示 V 和 E

image-20210402142950001
有向图

$D=<V, E>$

  • 其中 $V\neq \empty$ 称为顶点集，其元素称为顶点或结点；

  • E 是 V × V 的多重子集，称为边集，其元素称为有向边，简称边。

  • 有时用 V(D) 和 E(D) 分别表示 V 和 E

image-20210402145806354
关联与相邻（无向图）

关联：点和边

顶点相邻：顶点间有边

边相邻：两个边有公共端点

image-20210402150329267
关联与相邻（有向图）

顶点相邻：顶点间有边

边相邻：两个边头对屁股

image-20210402150350126
特殊的图

有限图: V, E 都是有穷集合的图

n 阶图: n 个顶点的图

零图: E = 空集的图

平凡图: 1 阶零图

空图: V = 空集的图

顶点的度数与握手定理（重点）

顶点的度数（无向图）
image-20210402150439175
顶点的度数（有向图）
image-20210402150531044
握手定理

定理：任何图（无向图和有向图）的所有顶点度数之和都等于边数的 2 倍

​ 理解：在计算各顶点度数之和时, 每条边均提供 2 度, m 条边共提供 2m 度

推论：任何图（无向图和有向图）都有偶数个奇度顶点

定理：有向图所有顶点的入度之和等于出度之和等于边数

​ 理解：每条边恰好提供 1 个入度和 1 个出度

事实上，一个度数列可图化当且仅当度数之和为偶数。

图的度数列（无向图）
image-20210402150637959
图的度数列（有向图）
image-20210402150657662
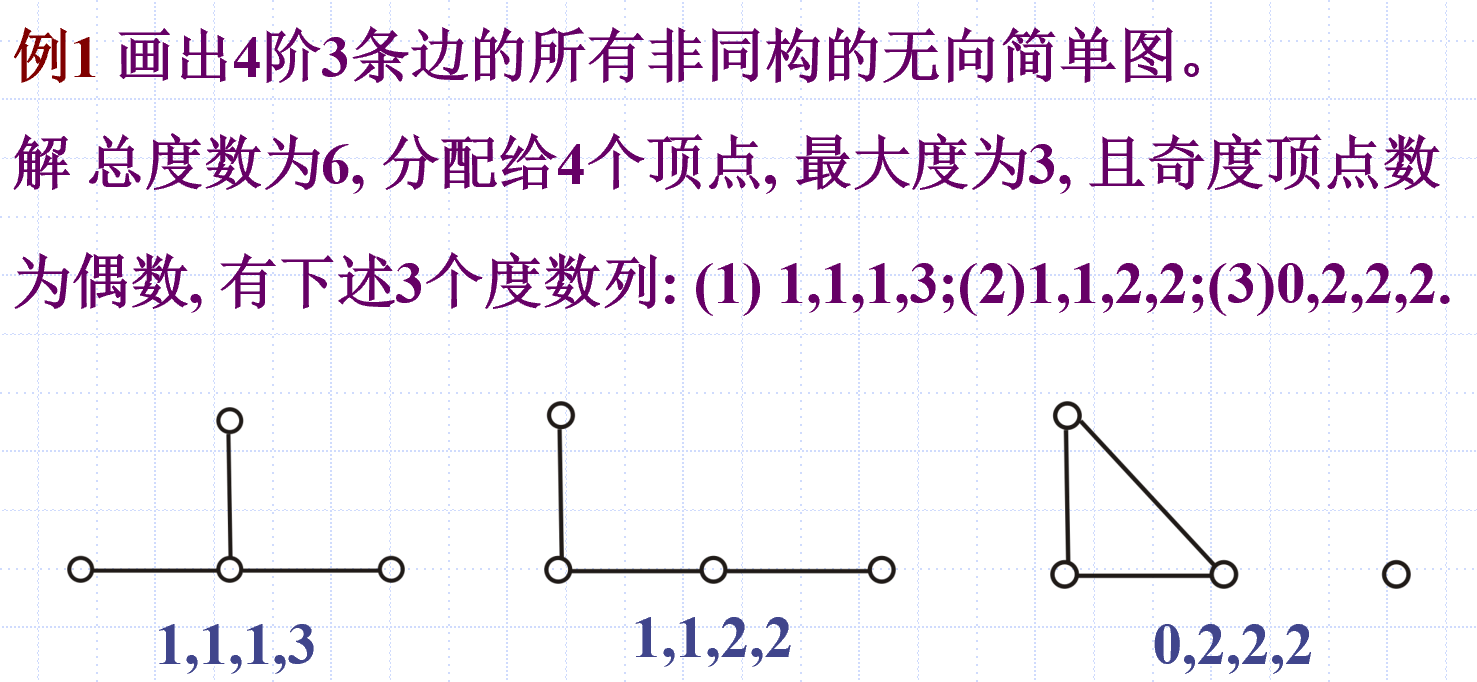
例
image-20210402145330286 image-20210402151120466 image-20210402151145746 image-20210402152403819 image-20210402152637525 image-20210402152836498

简单图、完全图、正则图、圈图、轮图、方体图

简单图

无向图中，关联同一对顶点的 2 条或 2 条以上的边, 称为平行边, 平行边的条数称为重数

在有向图中, 具有相同始点和终点的 2 条或 2 条以上的边称为有向平行边, 简称平行边, 平行边的条数称为重数

含平行边的图称为多重图

既无平行边也无环的图称为简单图

完全图
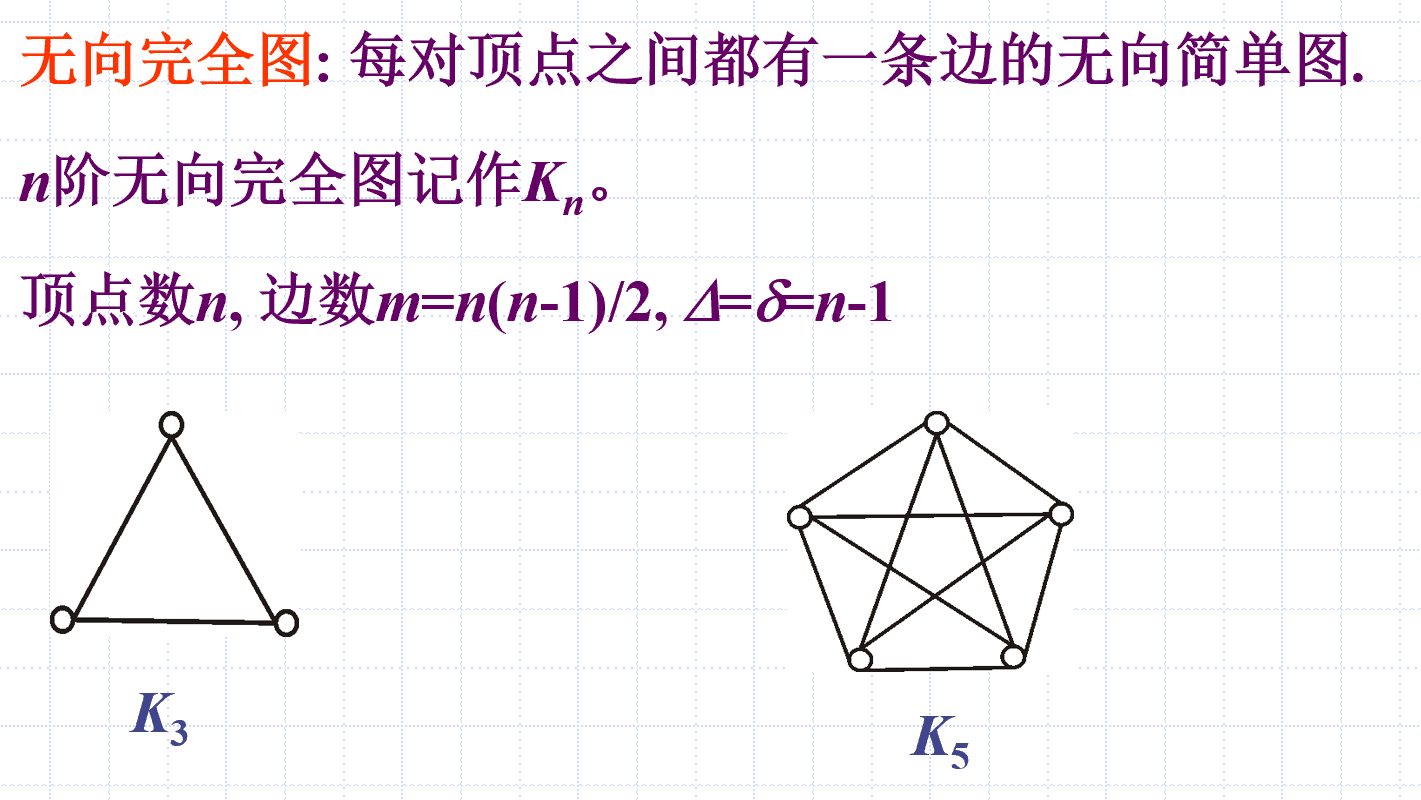
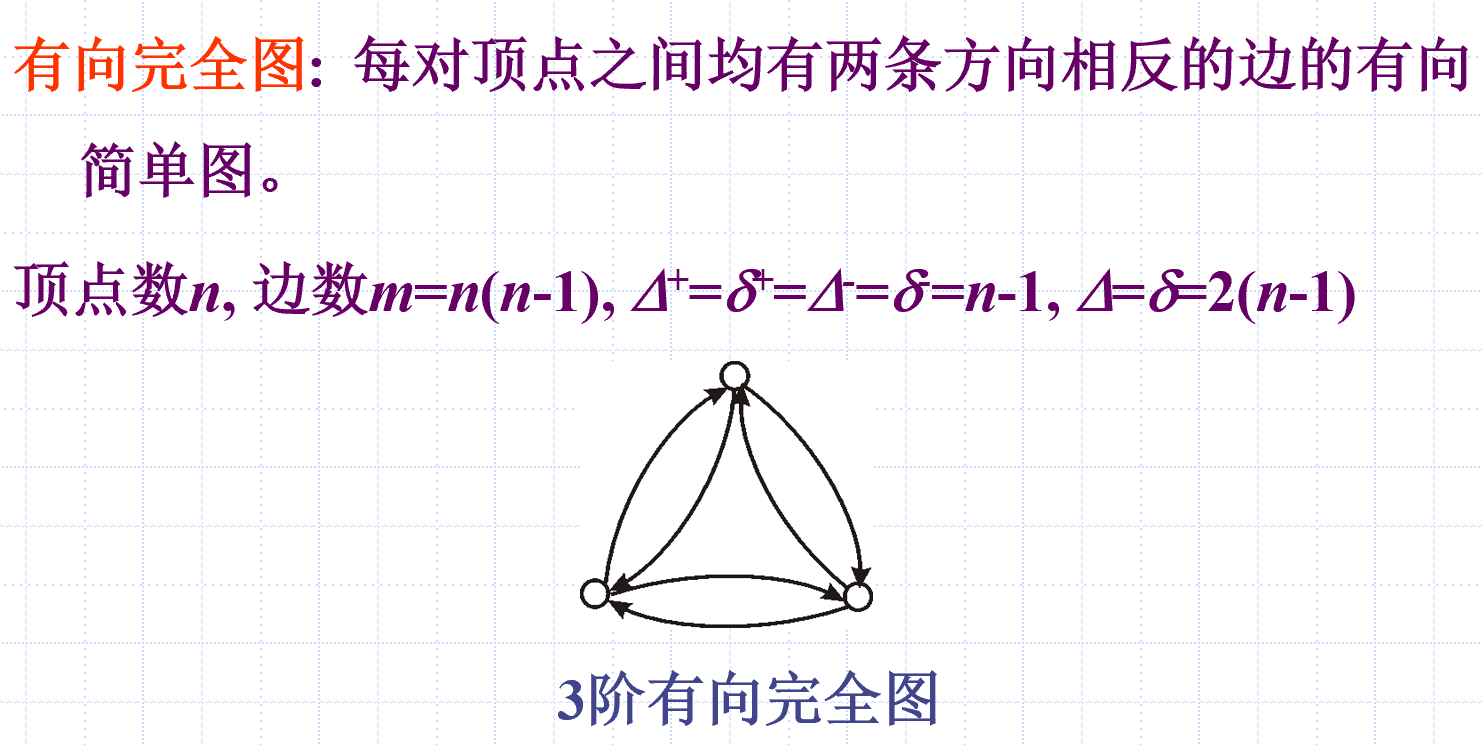
image-20210402153325549 image-20210402153347505
正则图
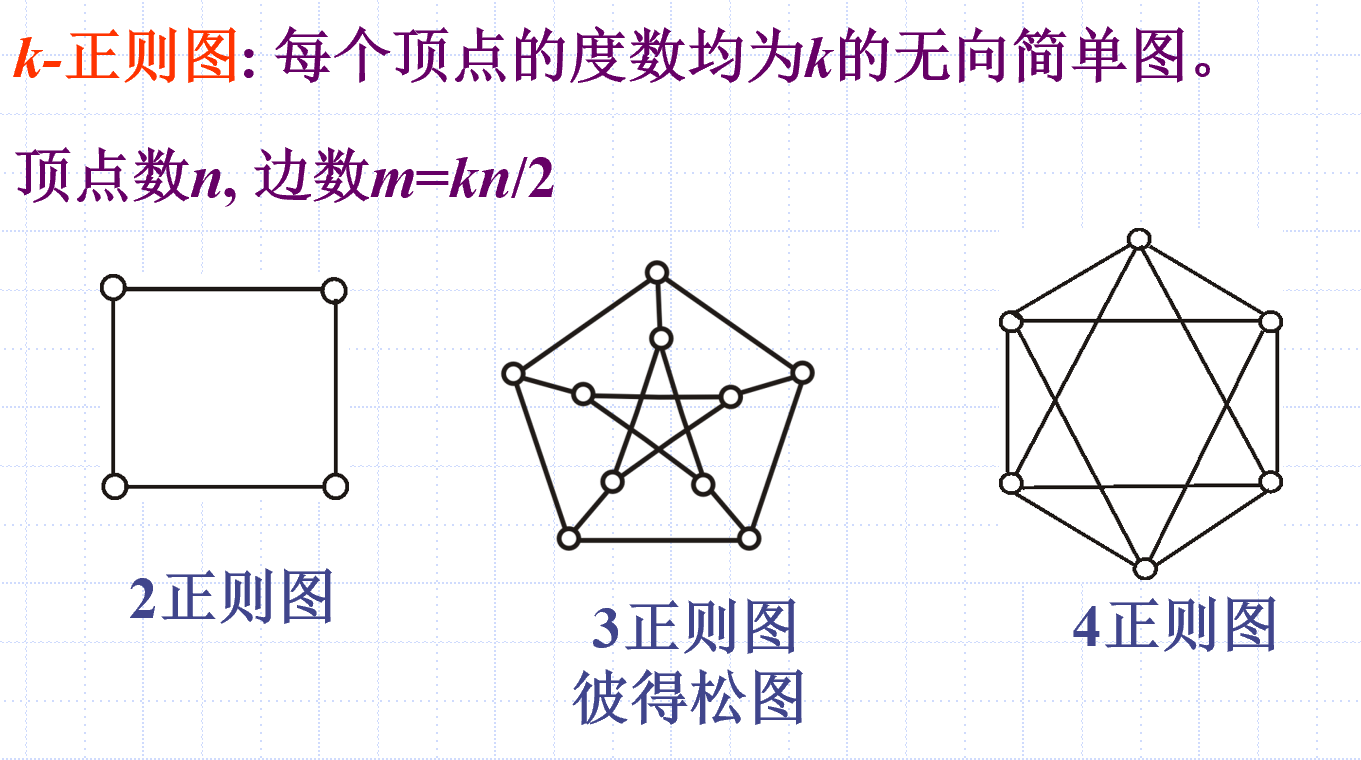
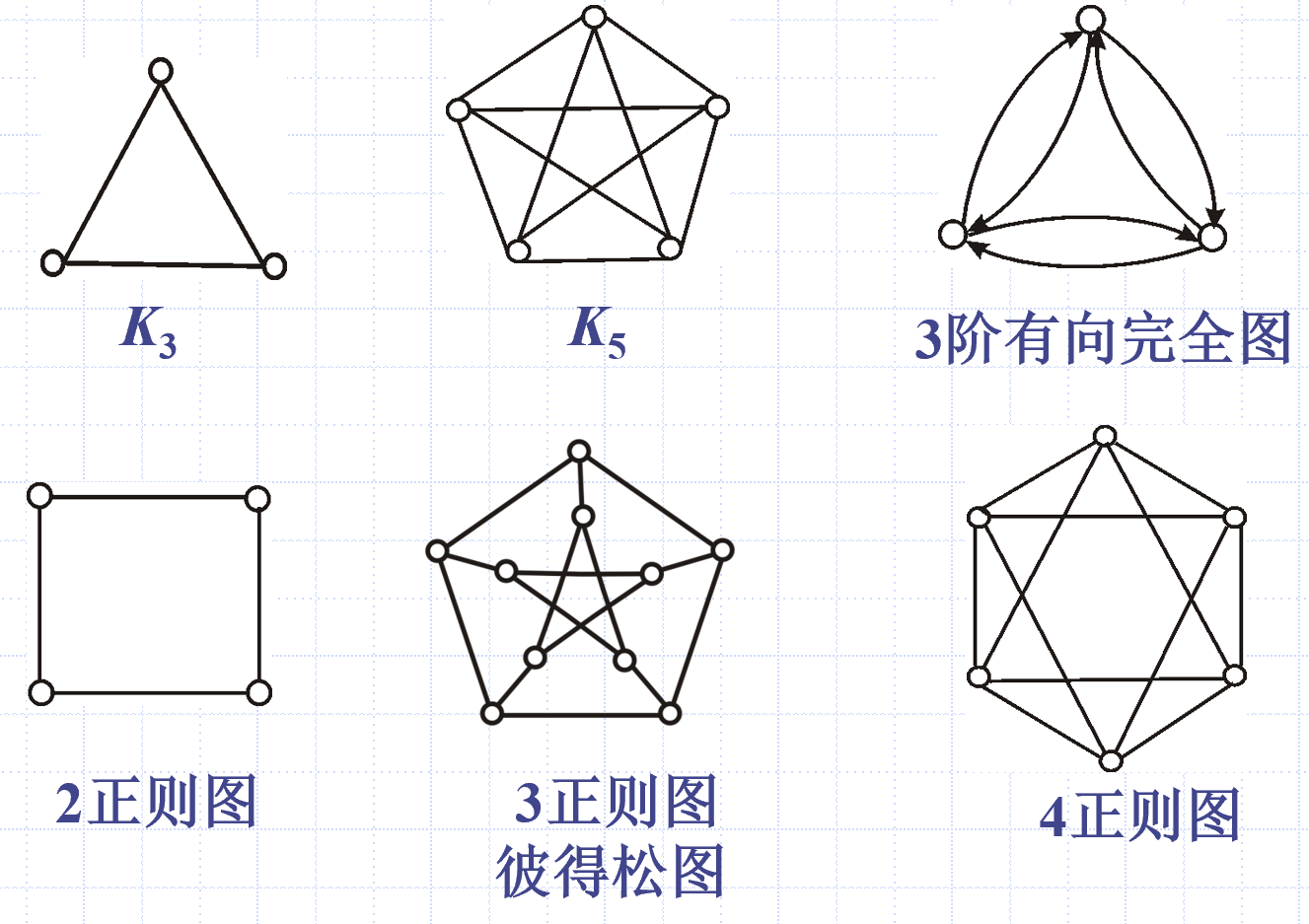
image-20210402153854260 image-20210402154016547
圈图
image-20210402154303391
轮图
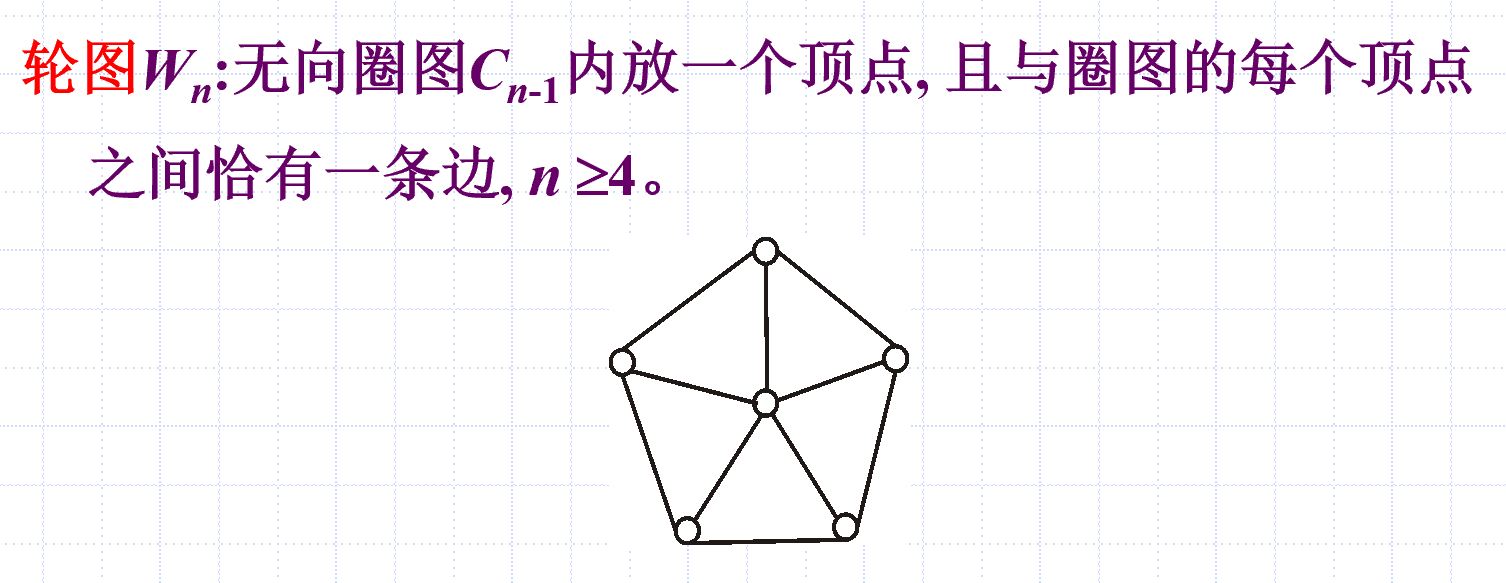
image-20210402154452349
方体图
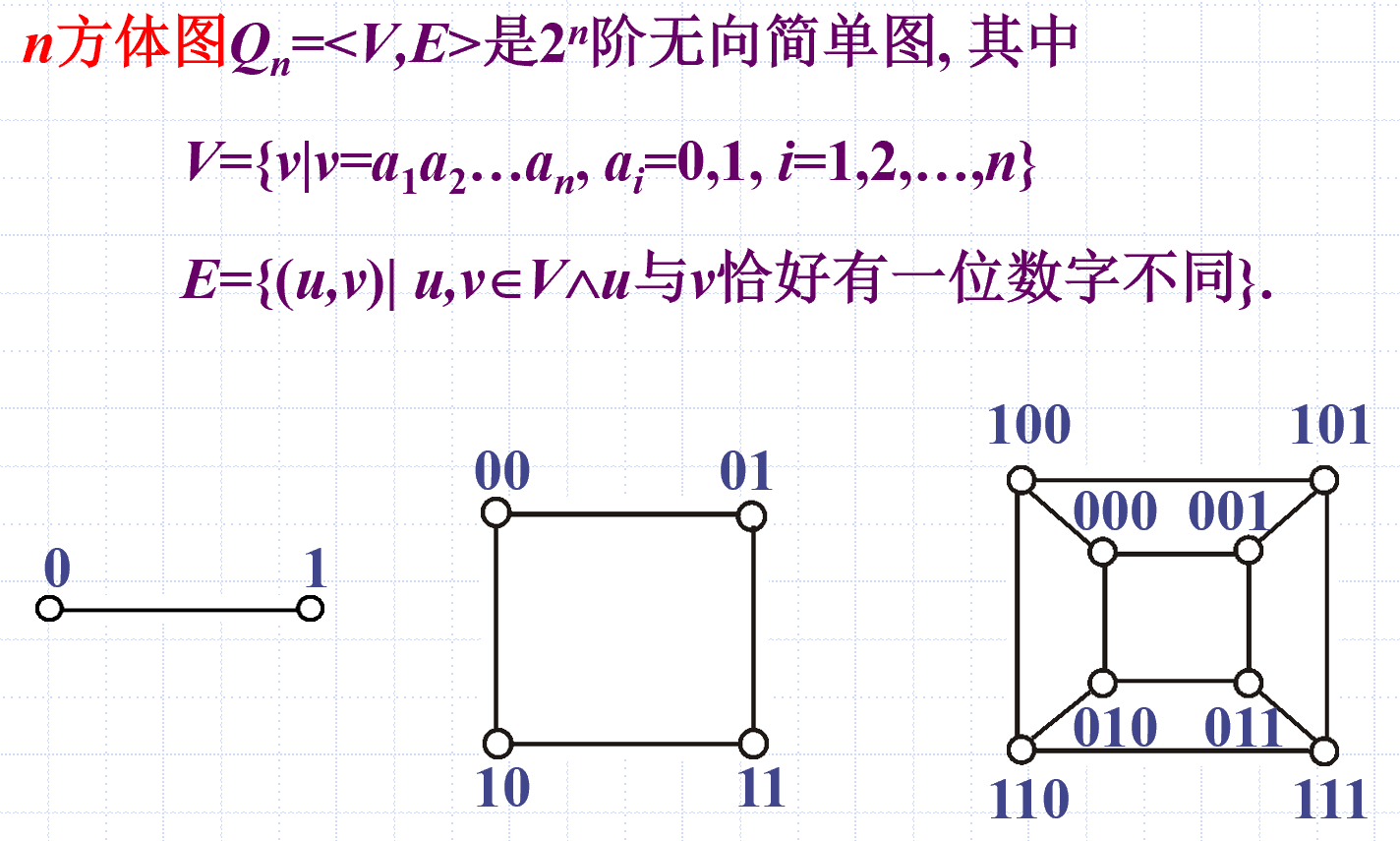
image-20210402154524725

子图、补图

子图
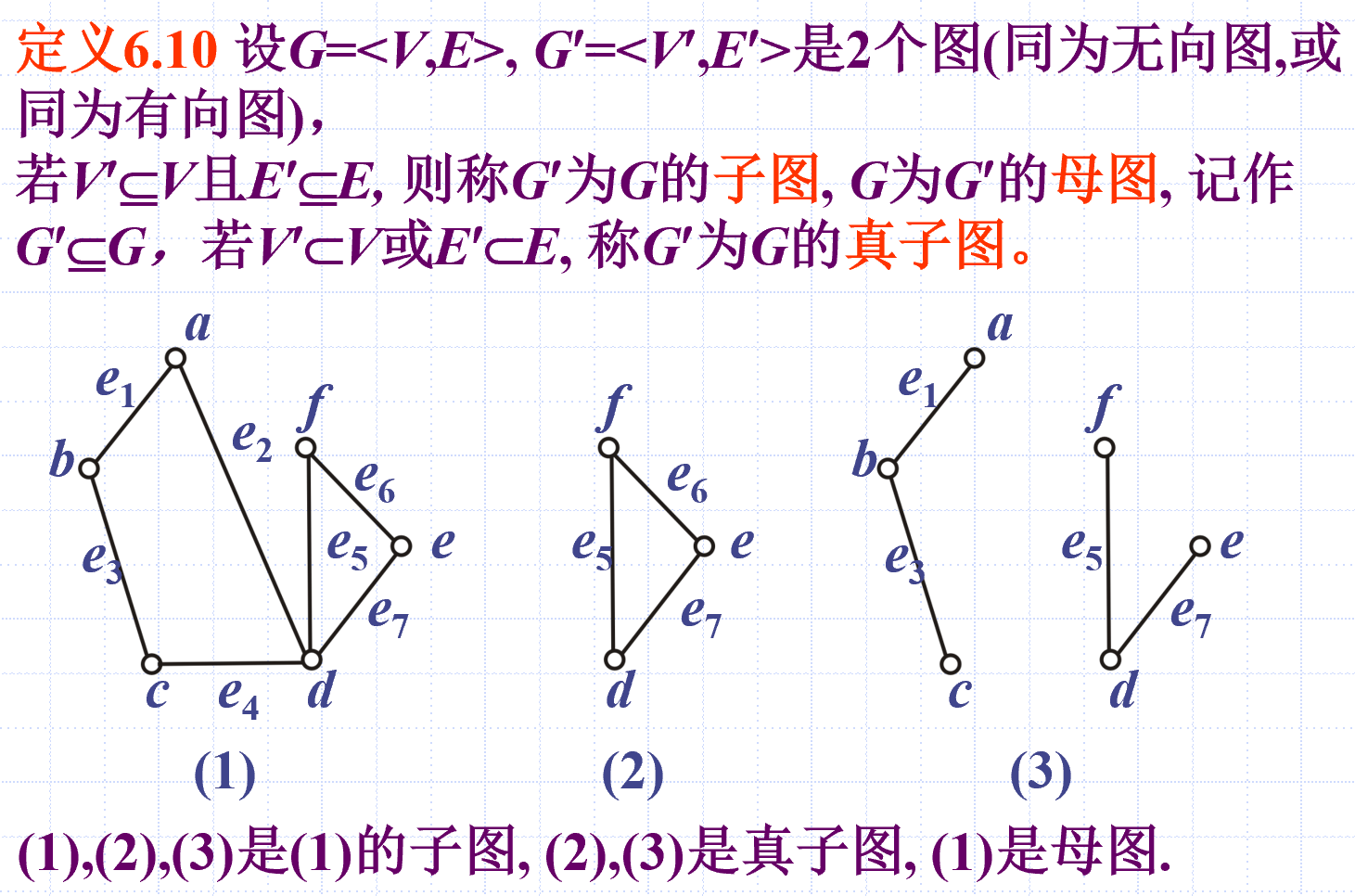
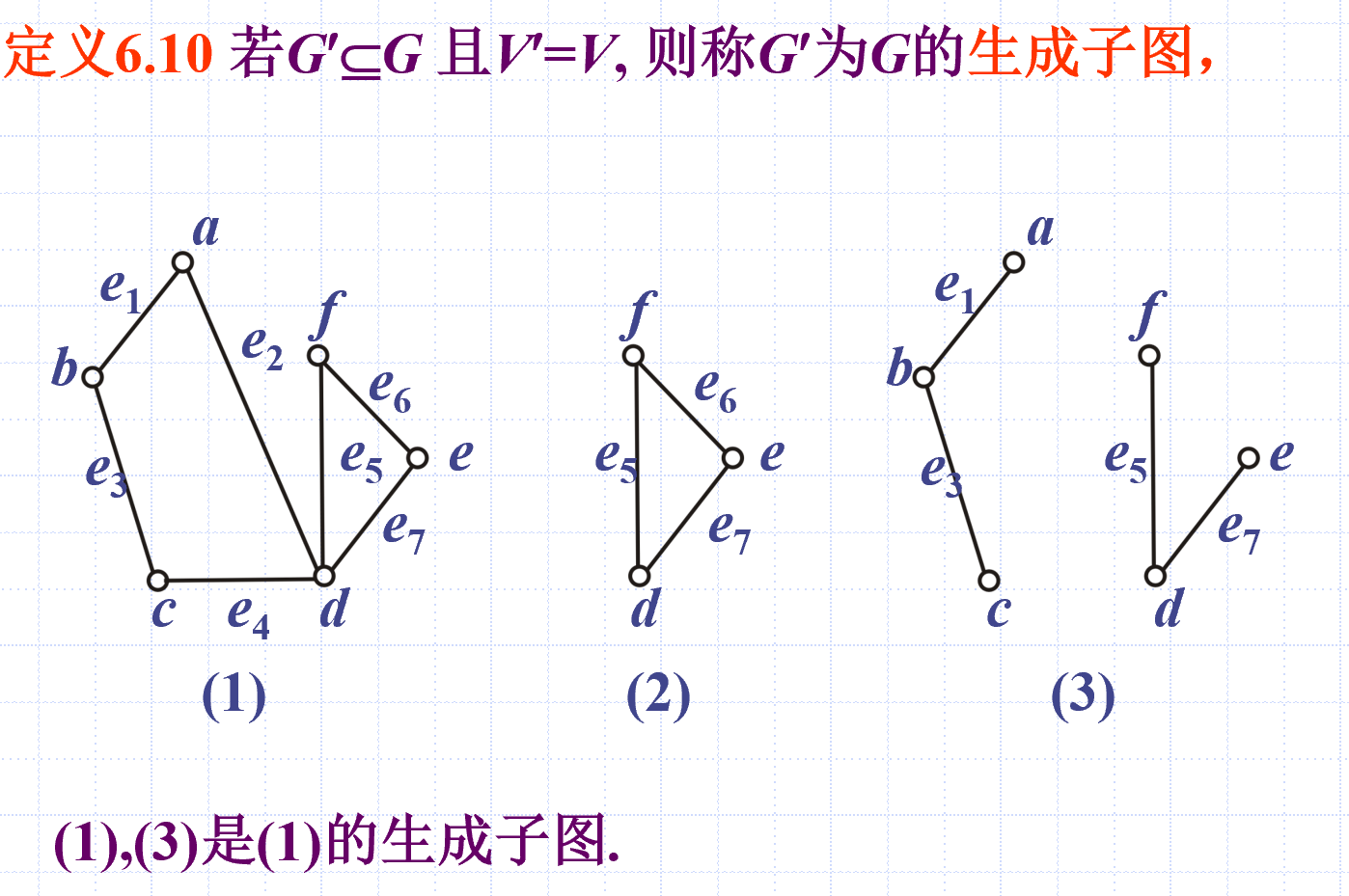
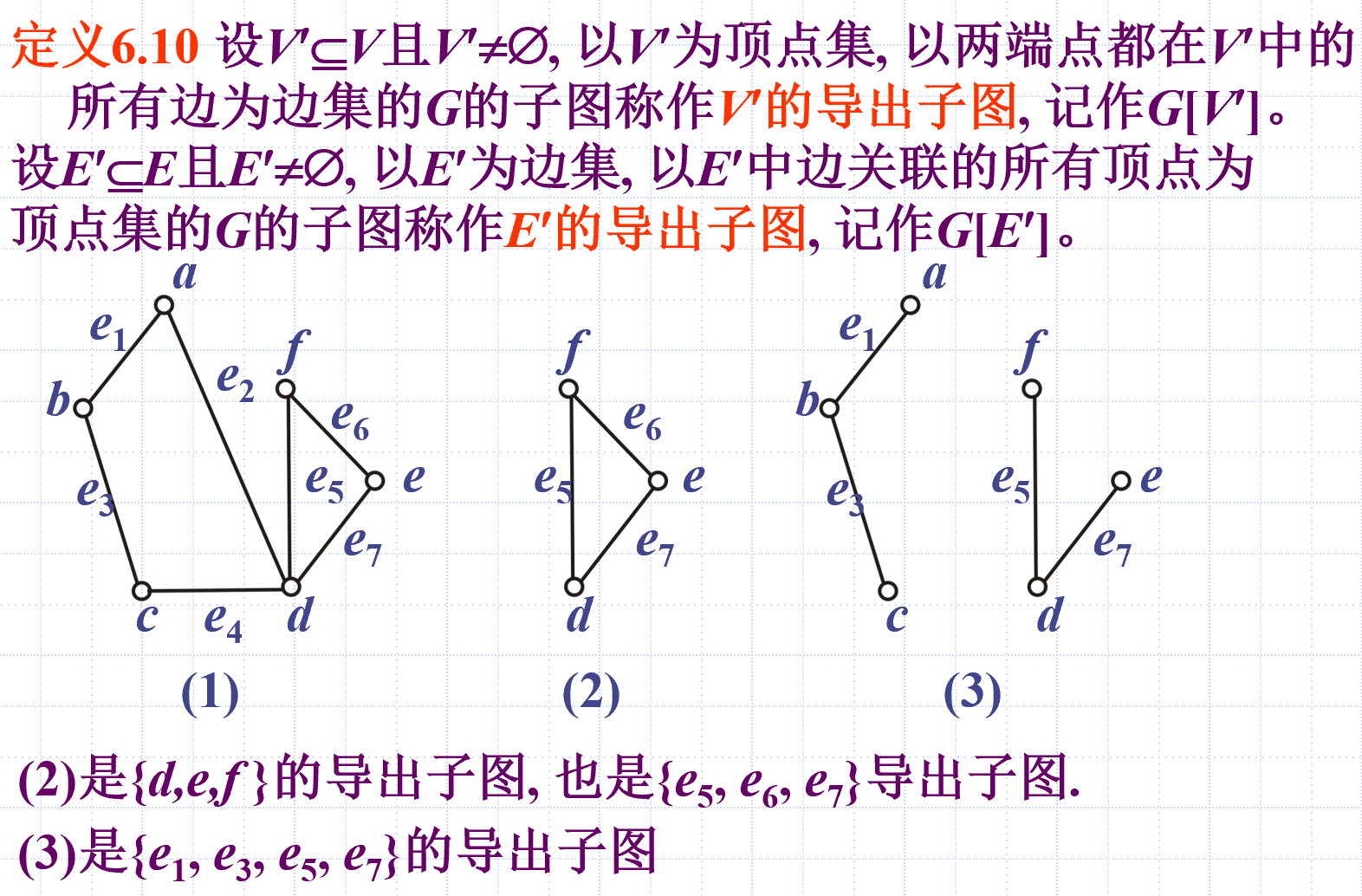
image-20210402160207106 image-20210402160332550 image-20210402160509835
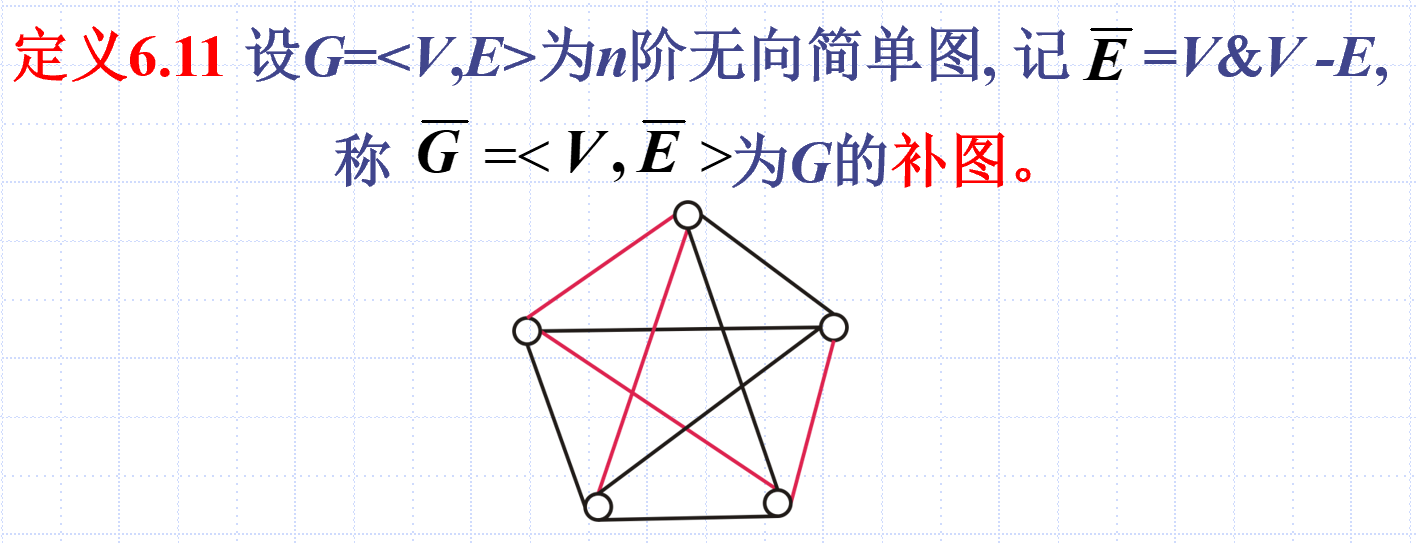
补图

顶点集合相同，边集合取补集

image-20210402160547246

图的同构 （重点）

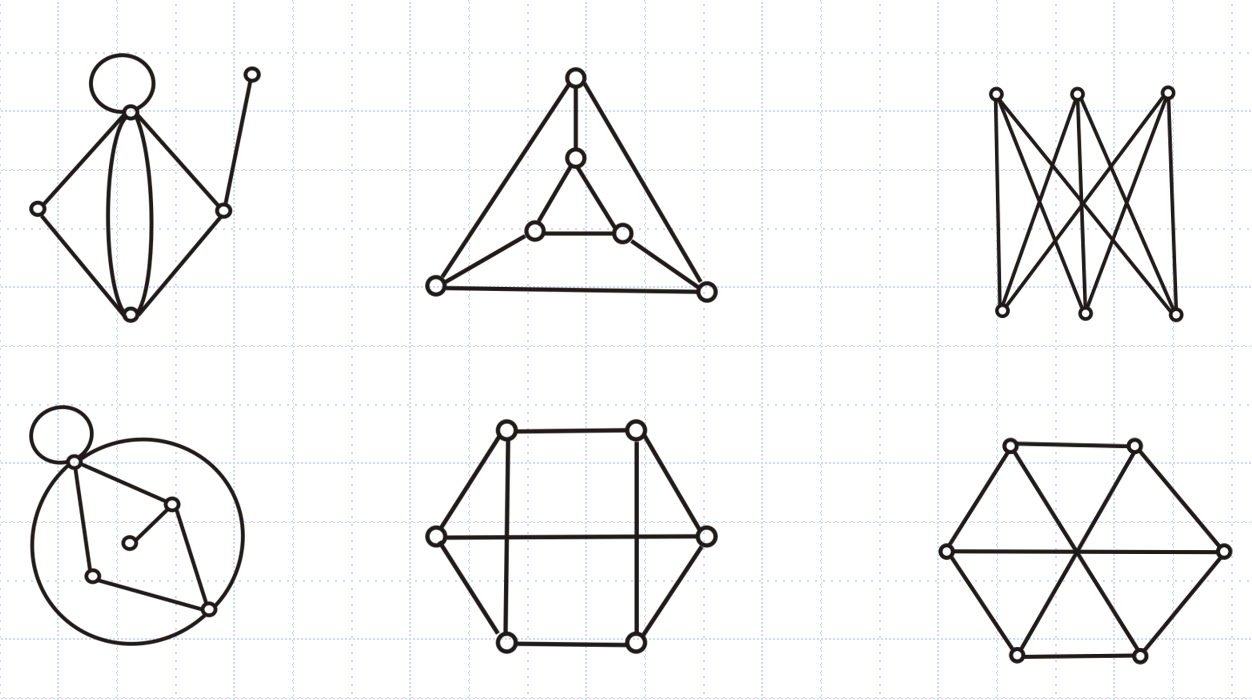
image-20210402160750328 image-20210402160813419 image-20210402161719665

连通性

通路与回路

定义

初级通 / 回路：点各异，更彻底

简单通 / 回路：边各异

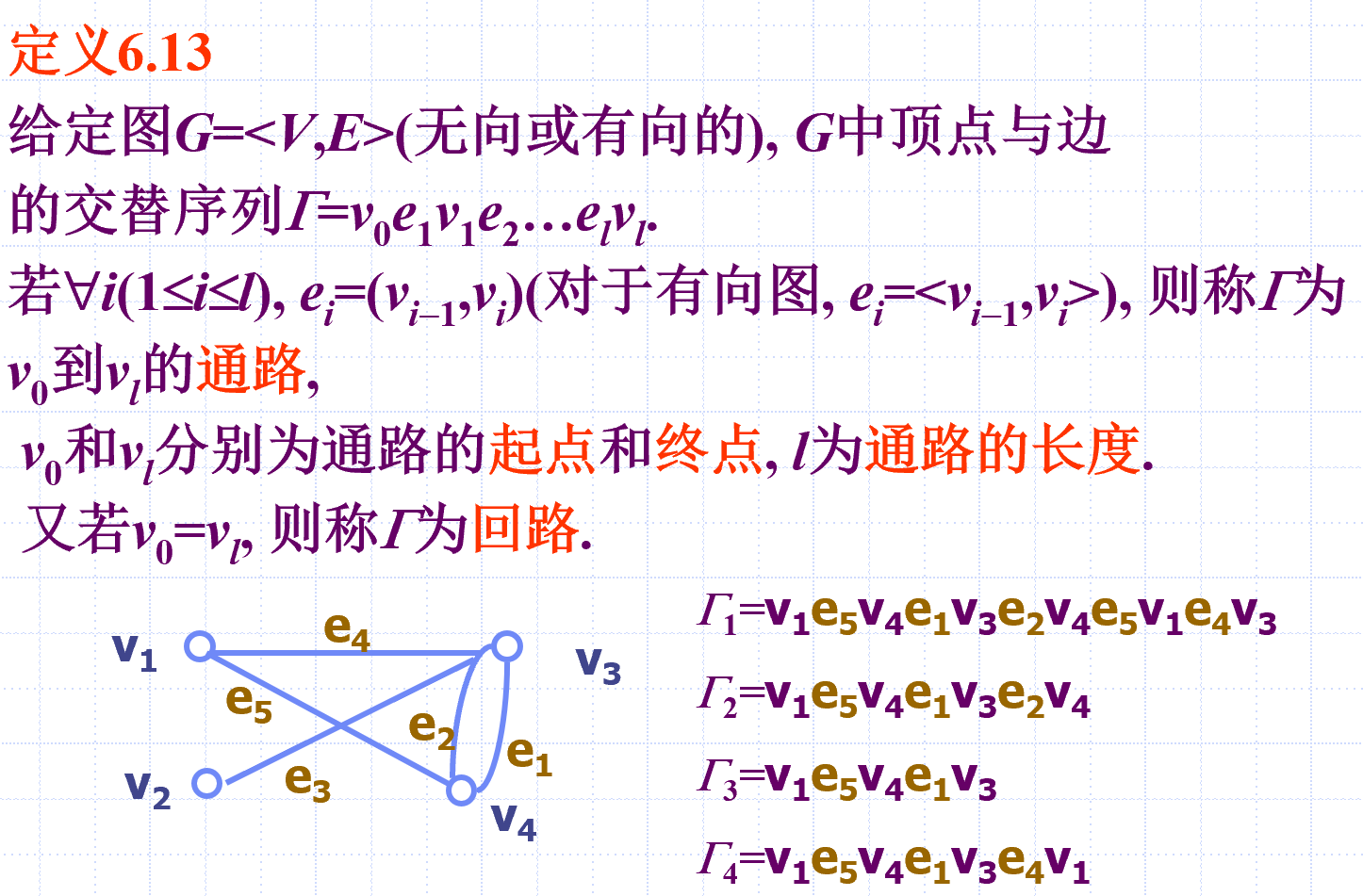
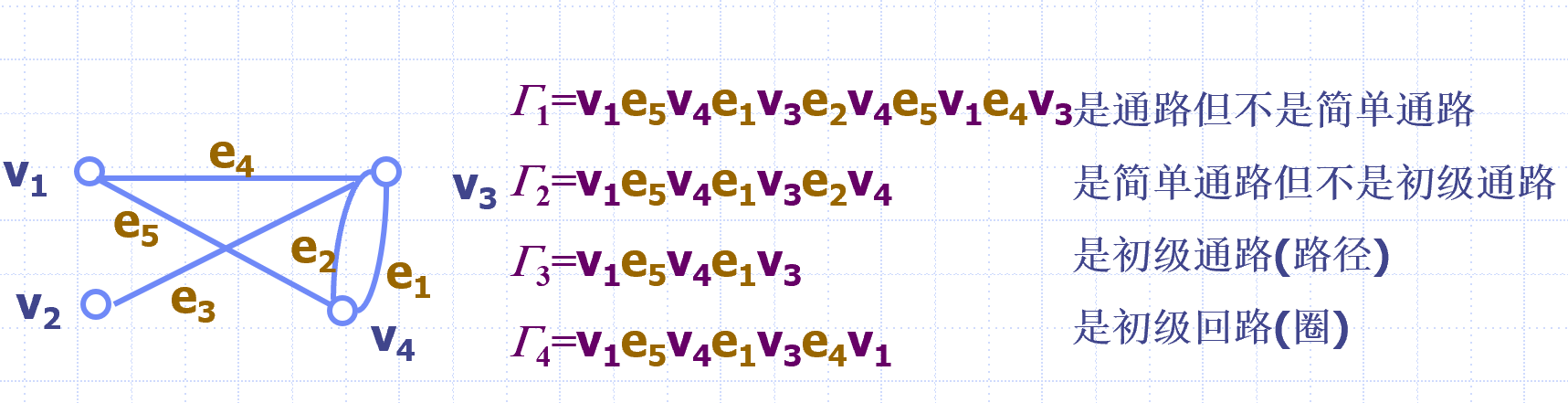
image-20210409142002634 image-20210409142303419 image-20210409142313630
说明
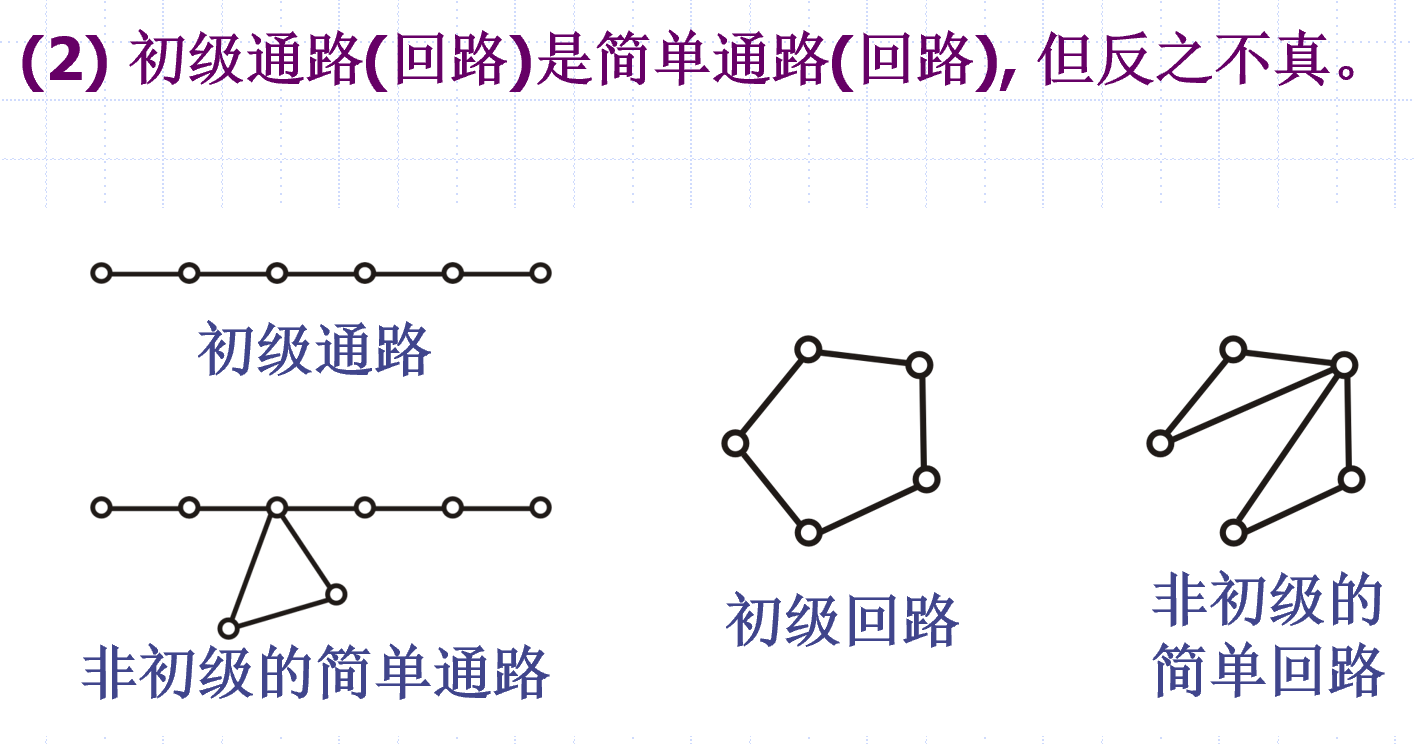
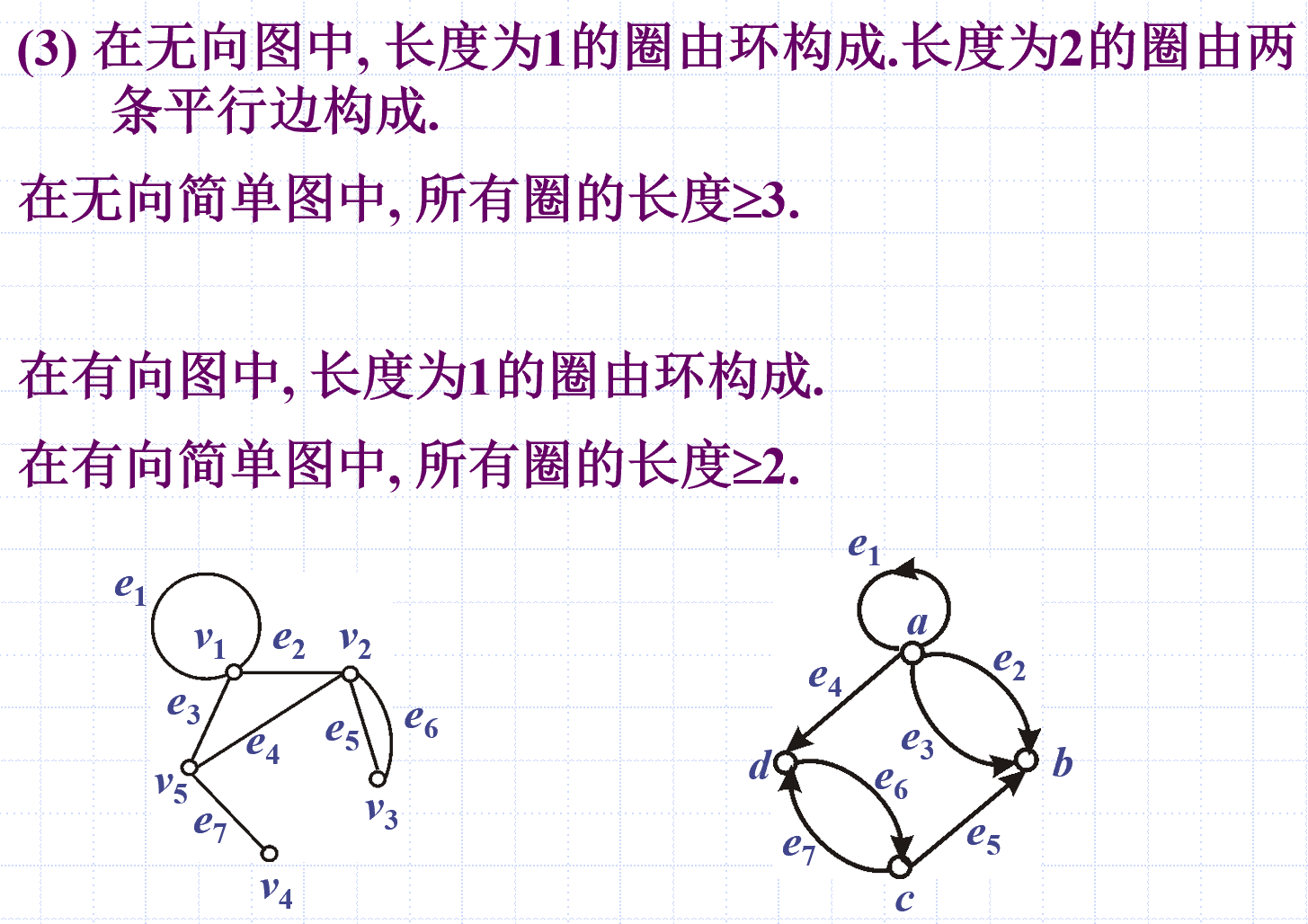
image-20210409142149426 image-20210409142436235 image-20210409142709693
定理
image-20210409142929924

无向图的连通性与连通度

定义
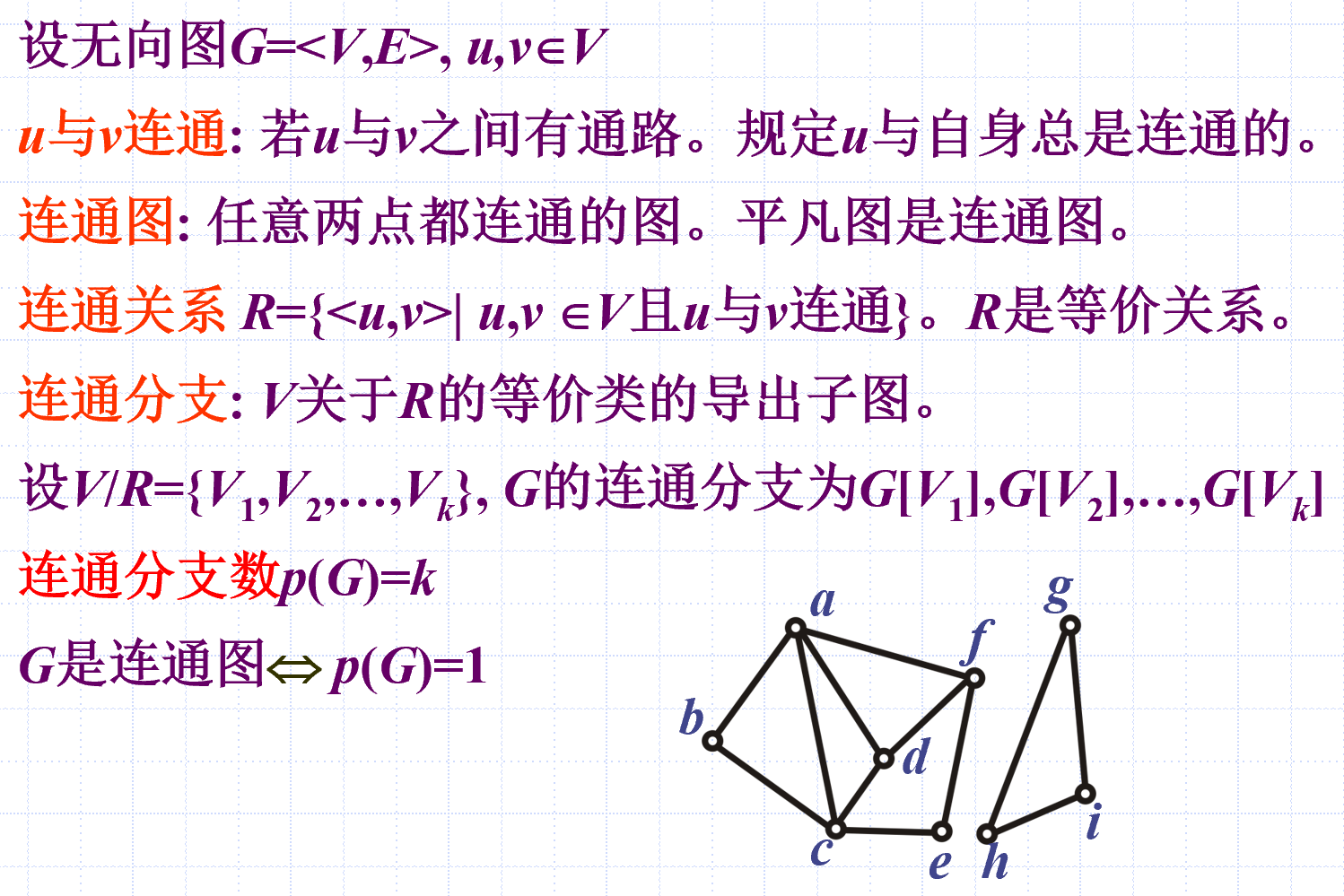
image-20210409143114024
例

连通分支并不是连通图独有，而是都有

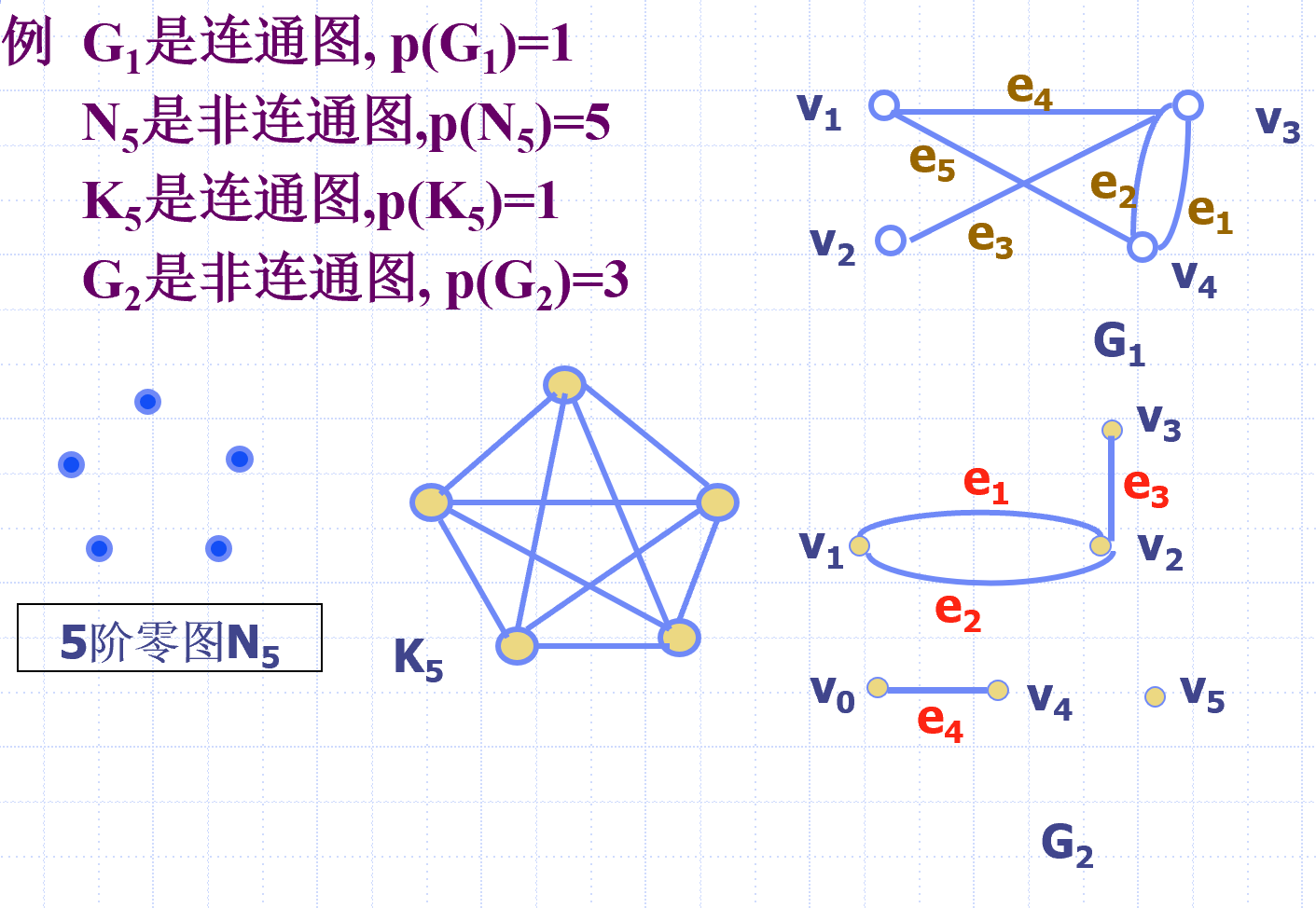
image-20210409144511496
短程线与距离
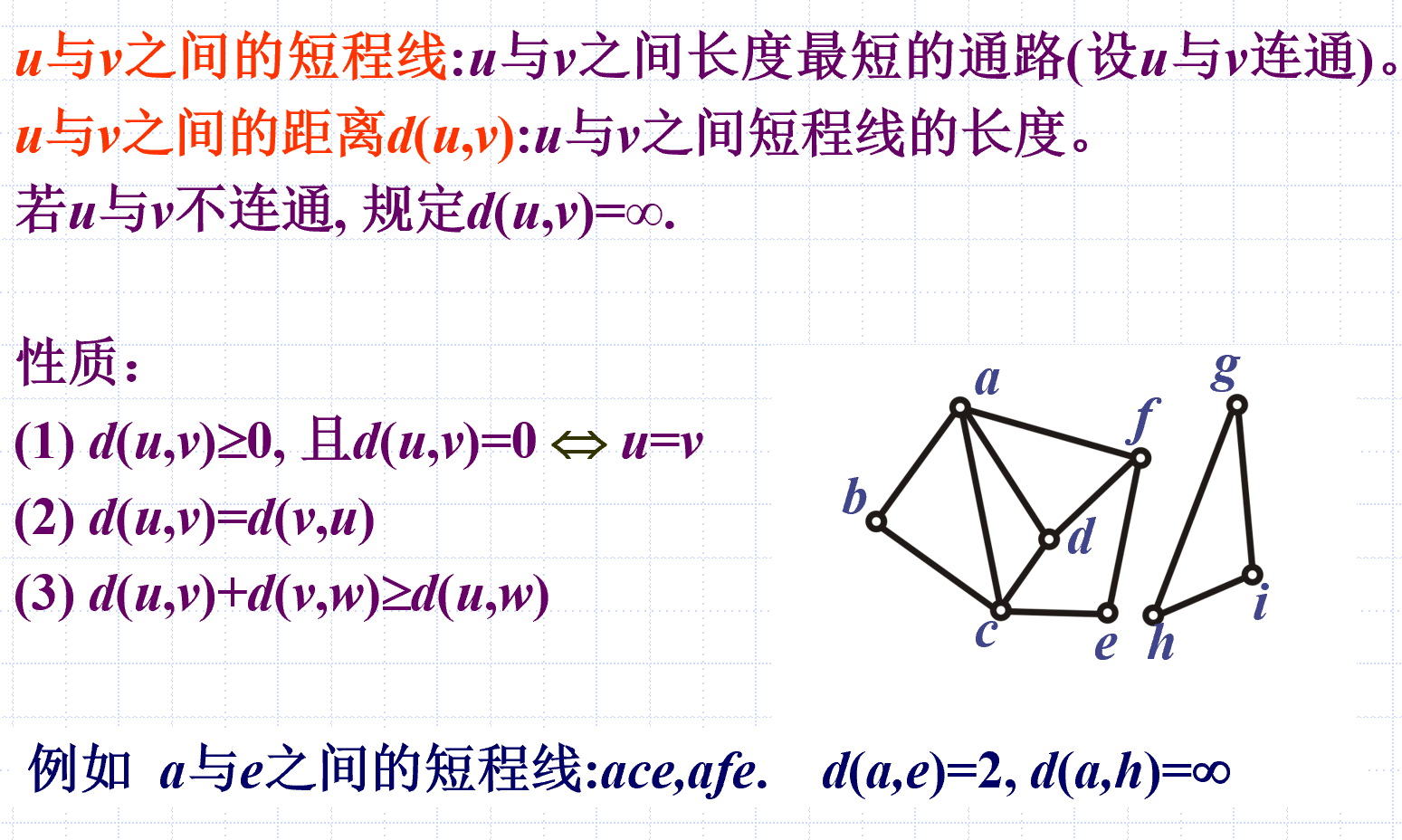
image-20210409143737571
定量评价连通性
image-20210409144824167
减号概念
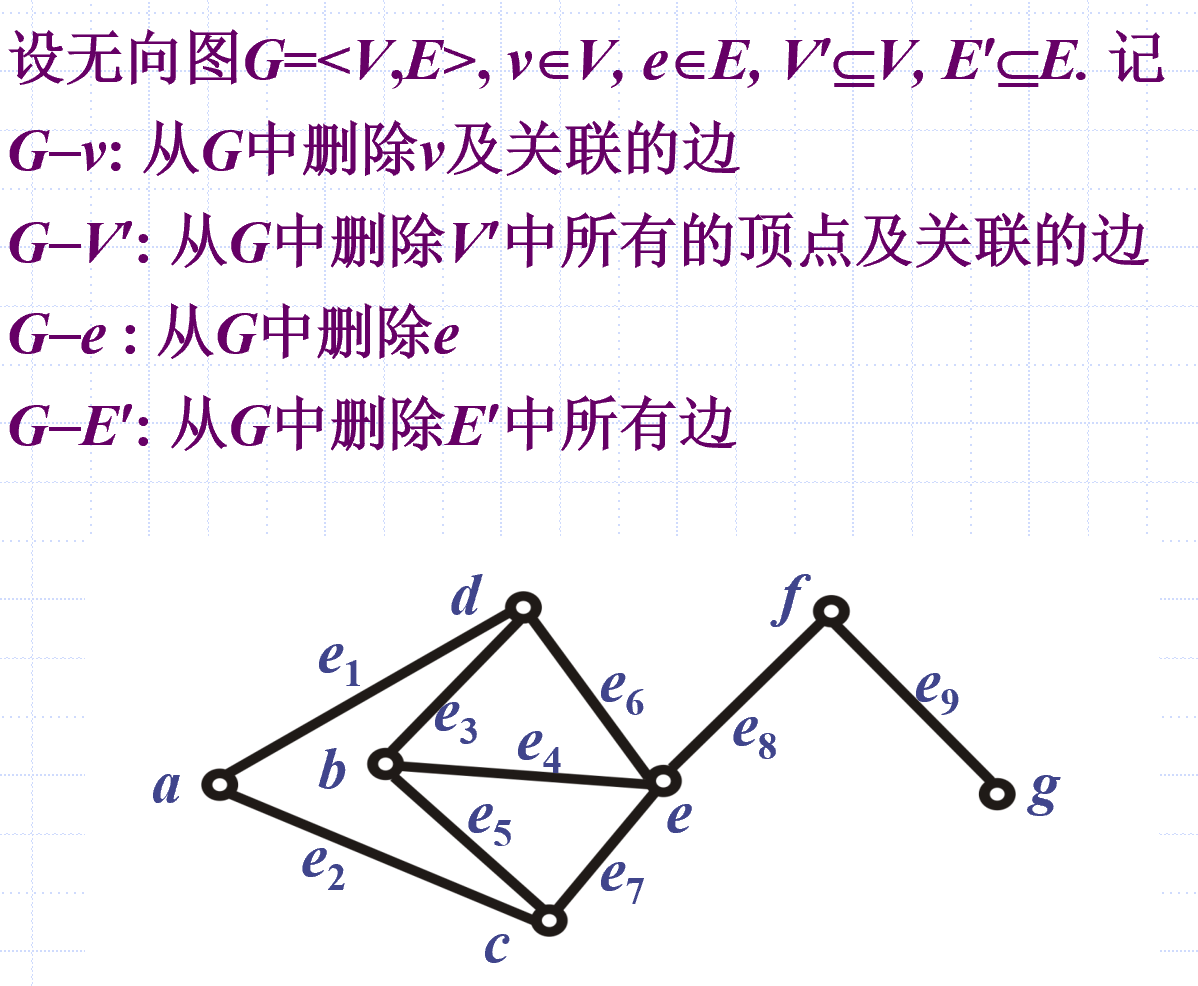
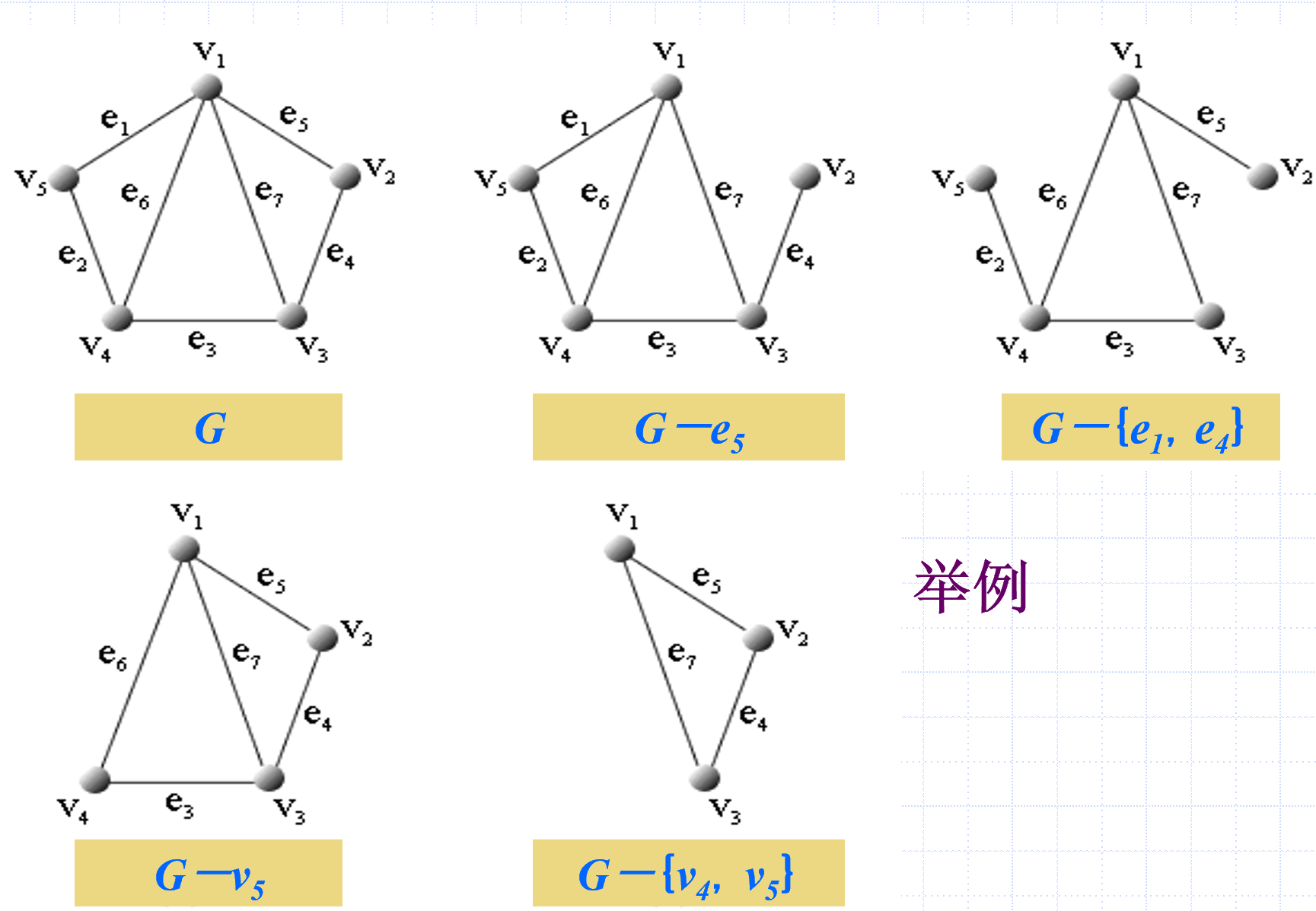
image-20210409144057082 image-20210409144134357
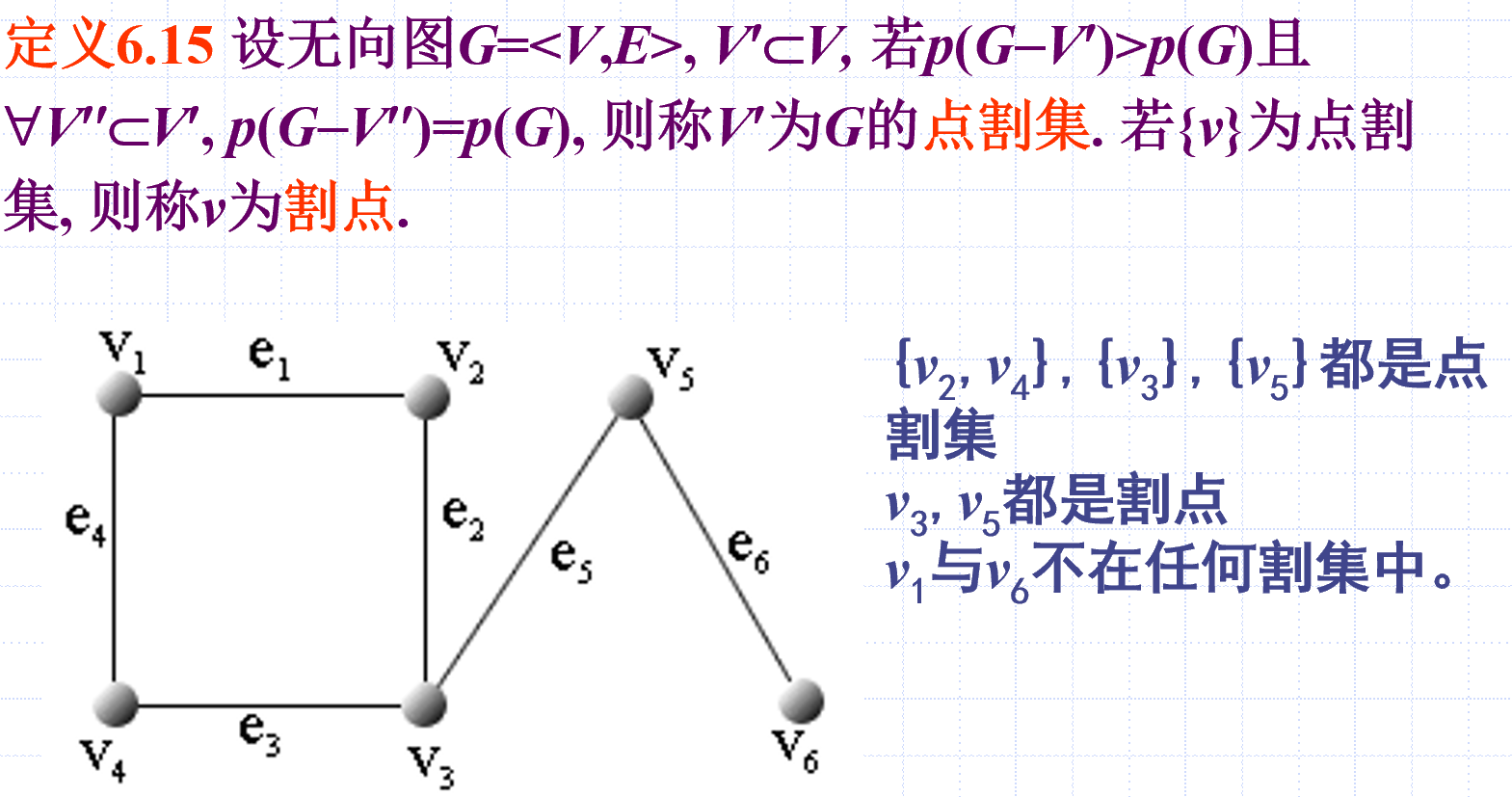
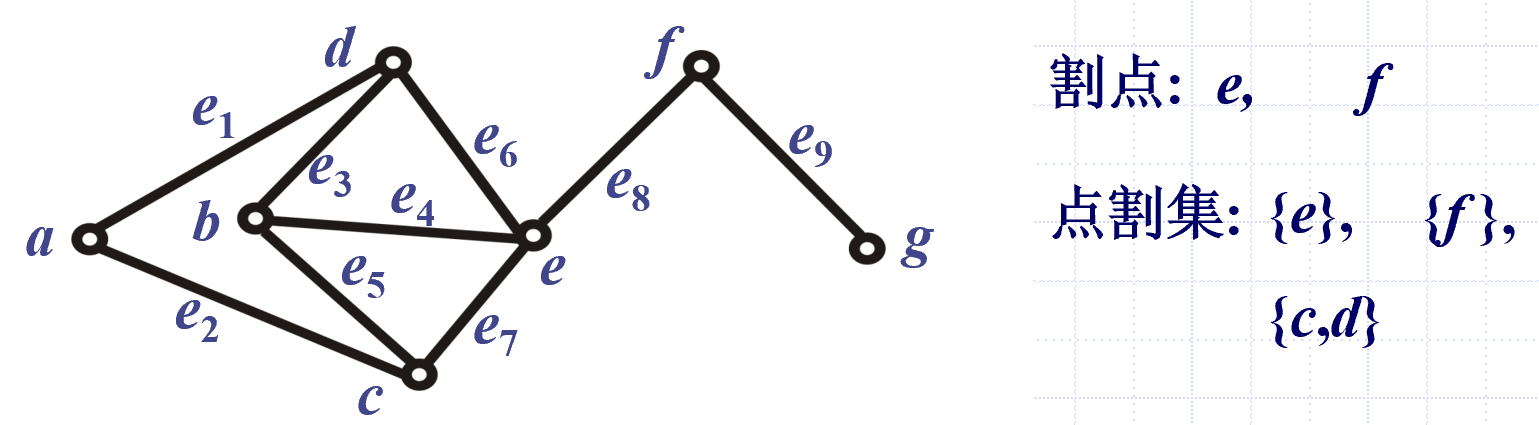
点割集

点割集：是个集合，点割集里的点被删掉后，图的连通分支数会增加，且点割集的子集不能是点割集

点割集只能是顶点集的真子集，因此完全图没有点割集

割点：只有一个元素的点割集

image-20210409144341148 image-20210409144419171
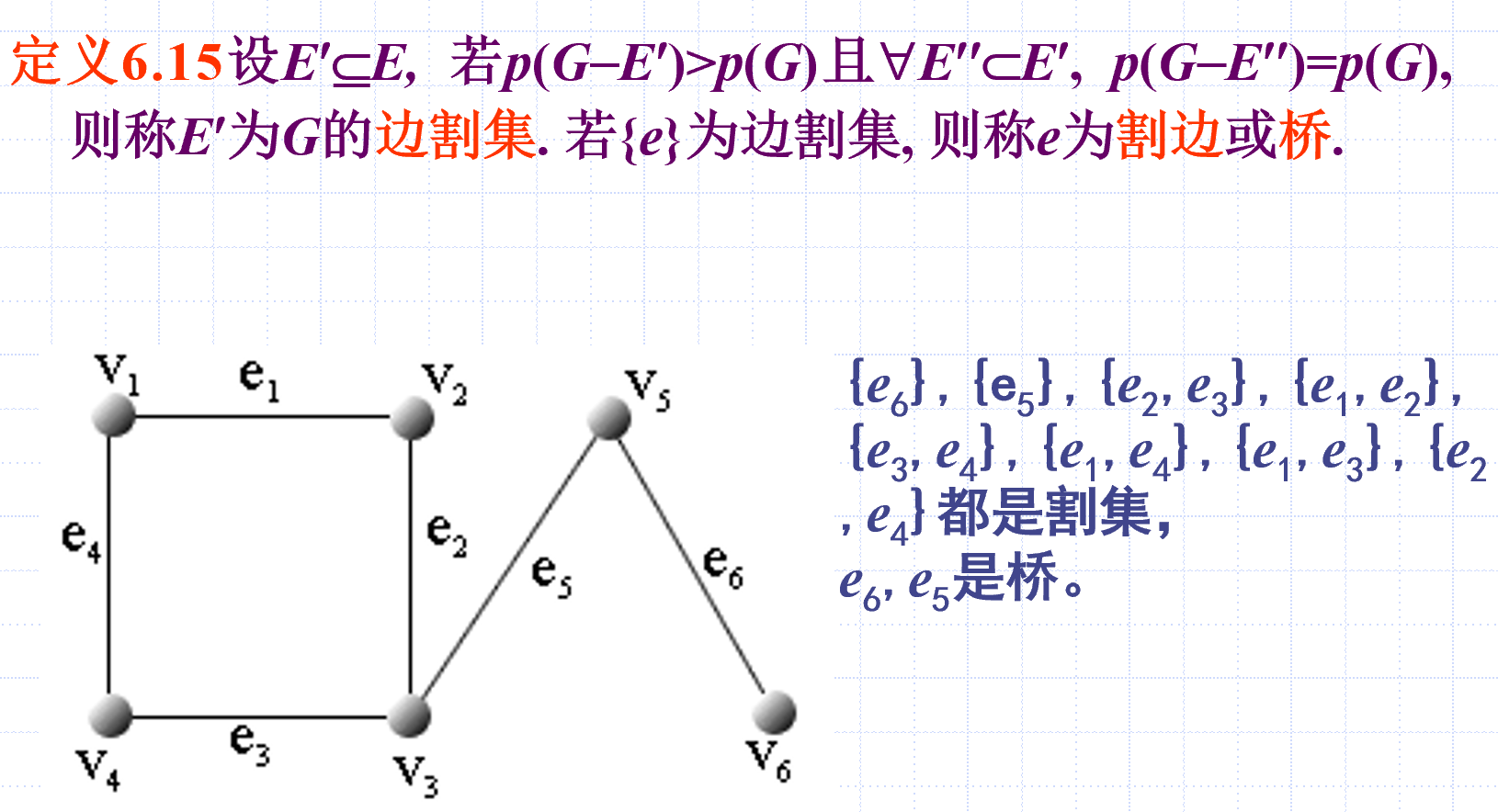
边割集

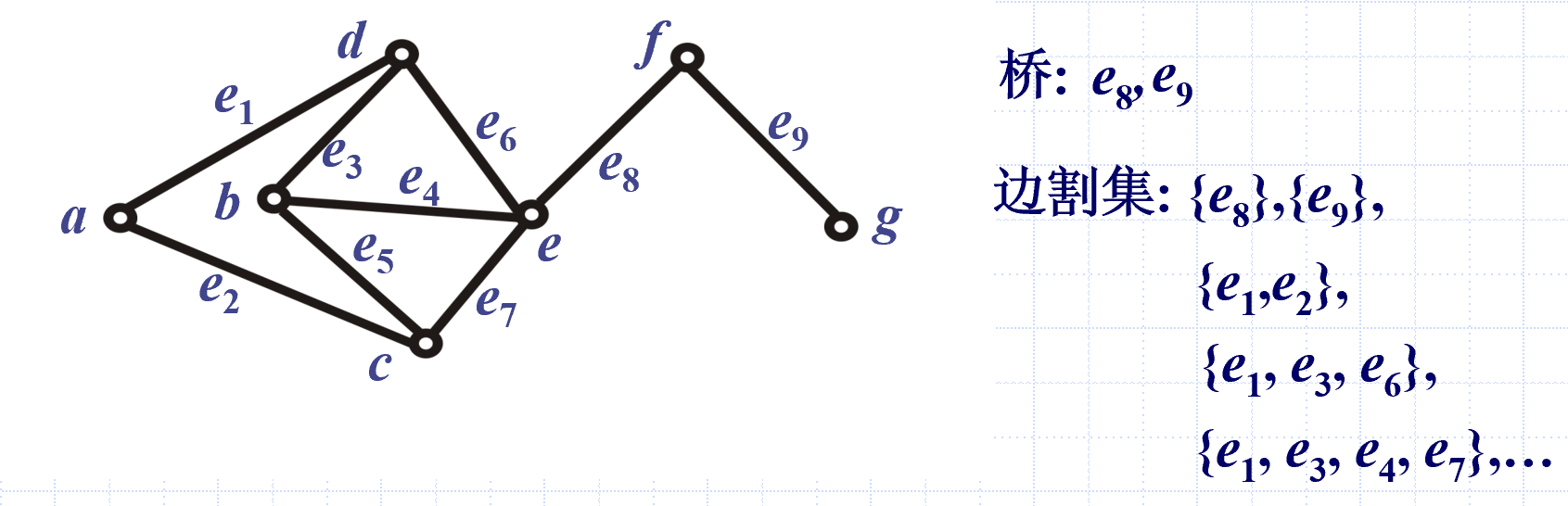
边割集是边集的子集

image-20210409144714678 image-20210409145020430
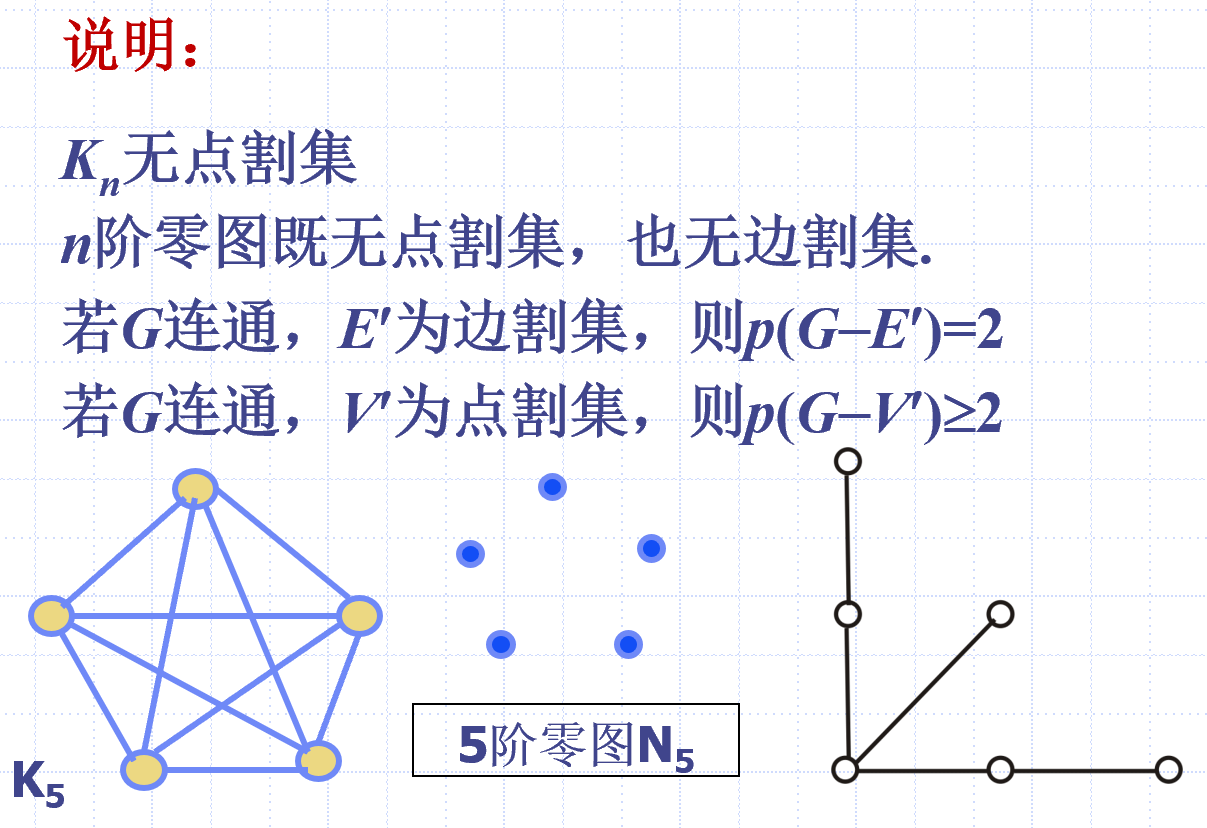
  • 完全图没有点割集
  • 零图没有点割集（删点变小）和边割集（无边）
  • 连通图删掉边割集后，p = 2；删点则不一定
image-20210409145124828
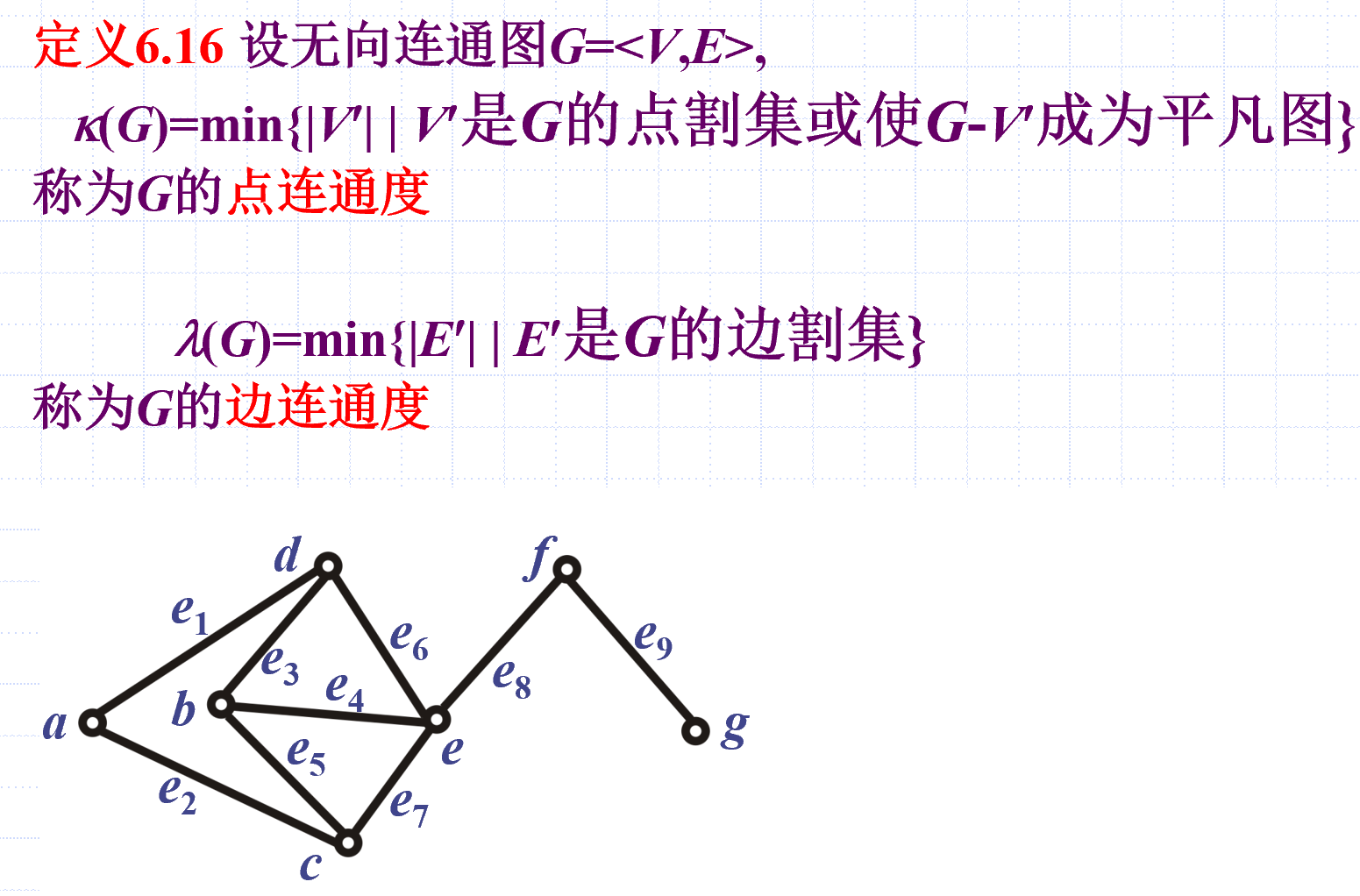
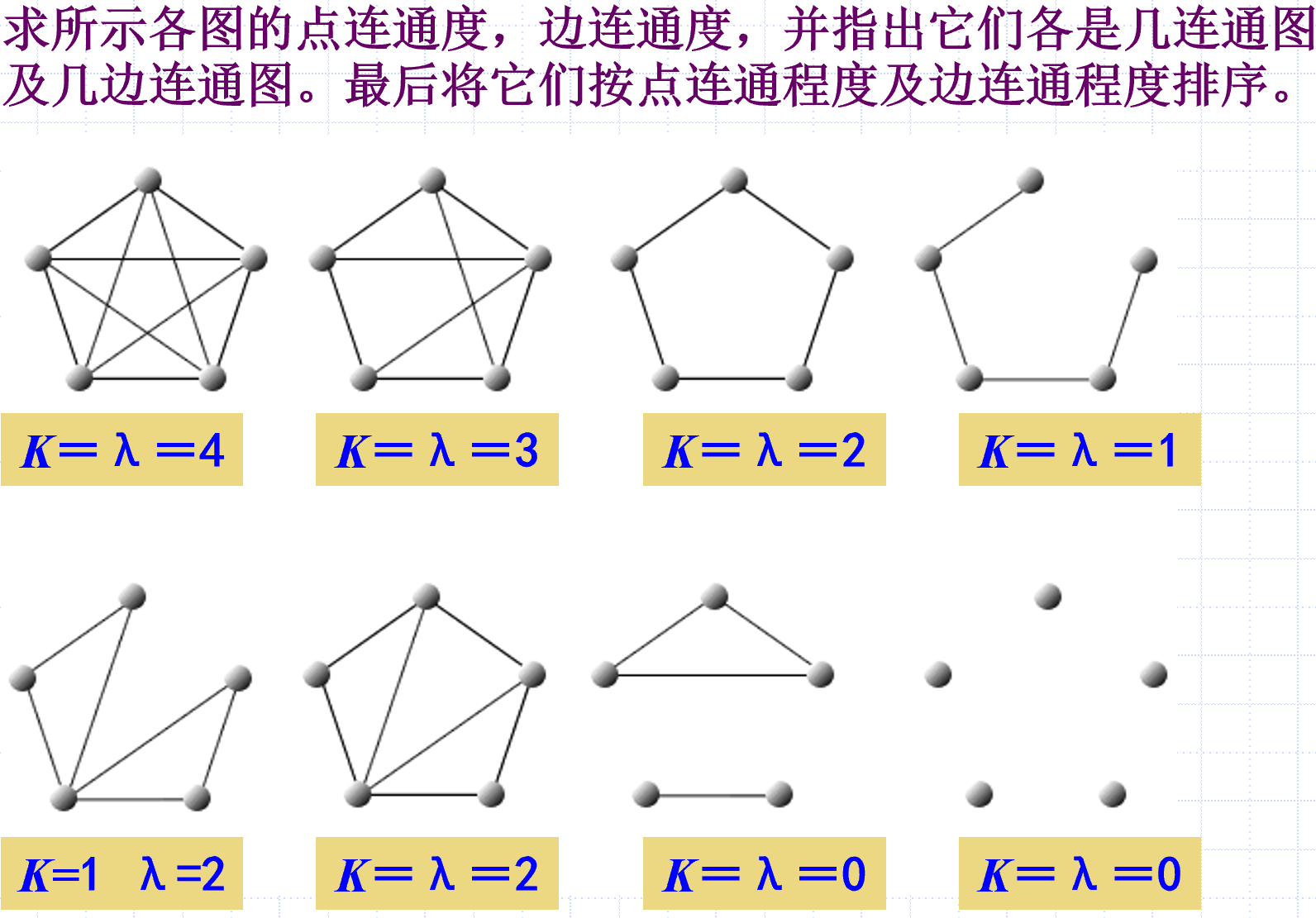
点连通度与边连通度

点连通度：长度最小的点割集的元素个数，或删点删到平凡图所删点的个数，两者取最小值

边连通度：长度最小的边割集的元素个数

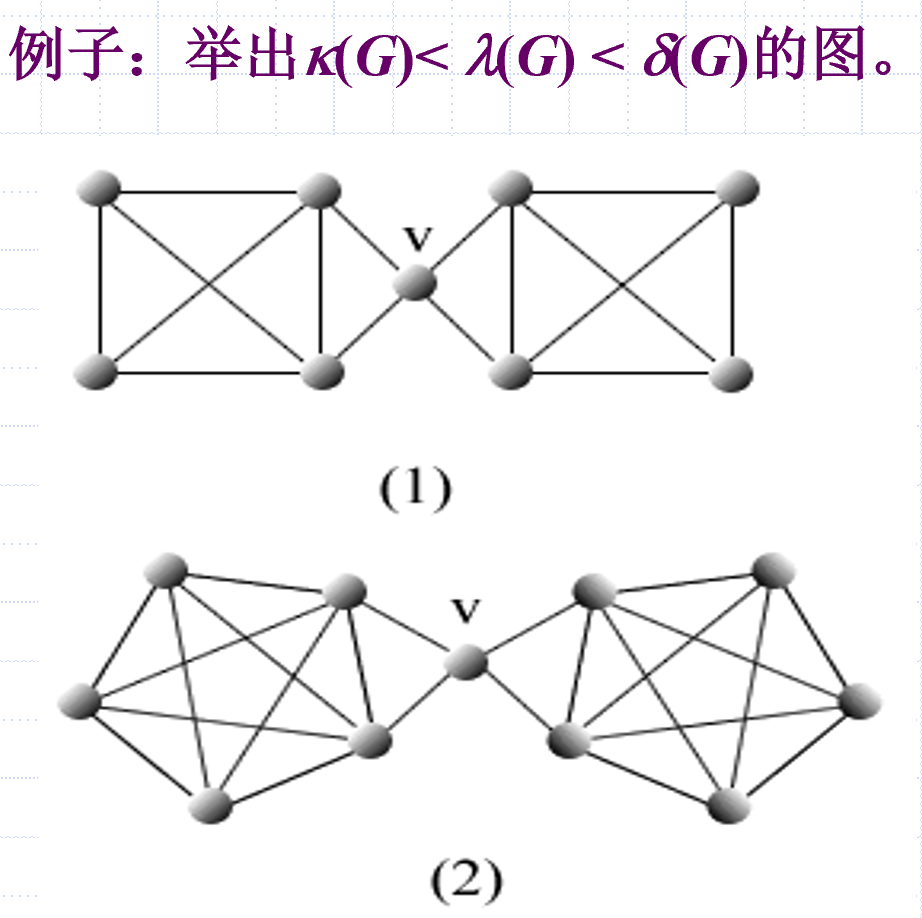
点连通度与边连通度不会大于最小度

image-20210409150844577 image-20210409150940312 image-20210409151019992 image-20210409151058852 image-20210409151122090

有向图的连通性及其分类

定义

有圈：强连通

有穿起所有点的线：单项连通

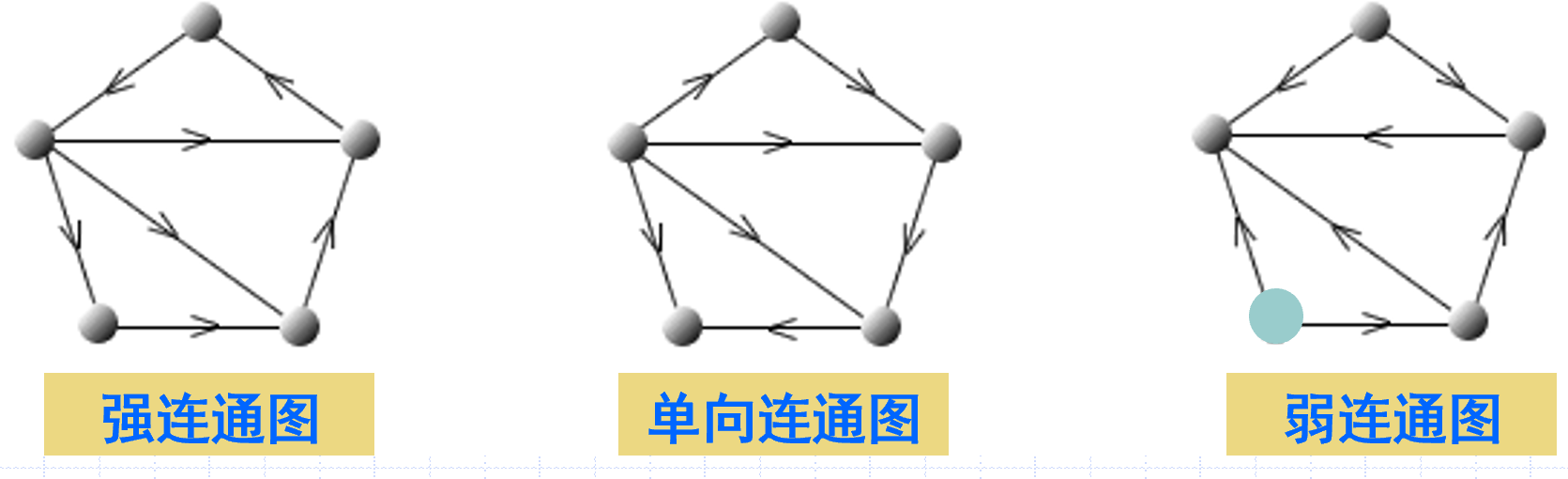
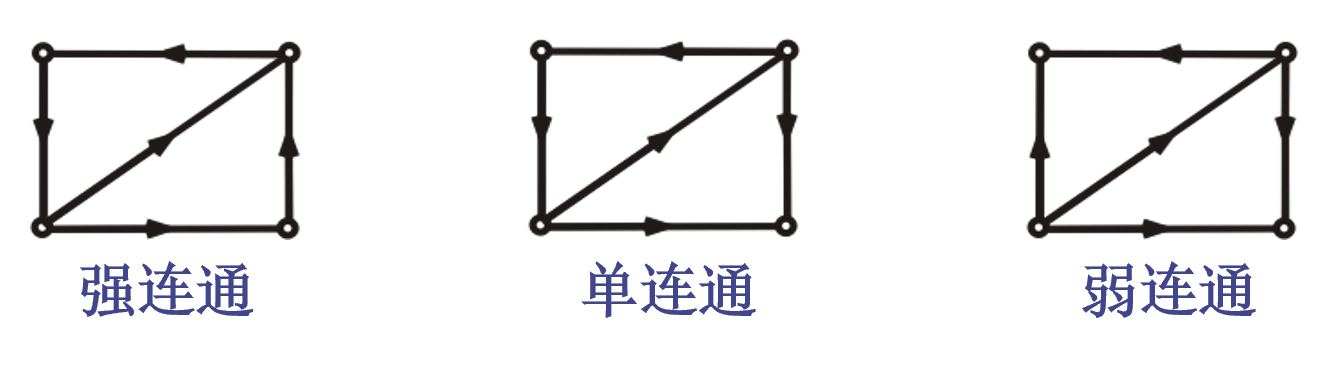
image-20210409151157864 image-20210409152202222 image-20210409152315962
强连通图与单向连通图的判定定理
image-20210409152415966
有向图中的短程线与距离
image-20210409154039670

矩阵表示

无向图的关联矩阵

行为点，列为边

定义
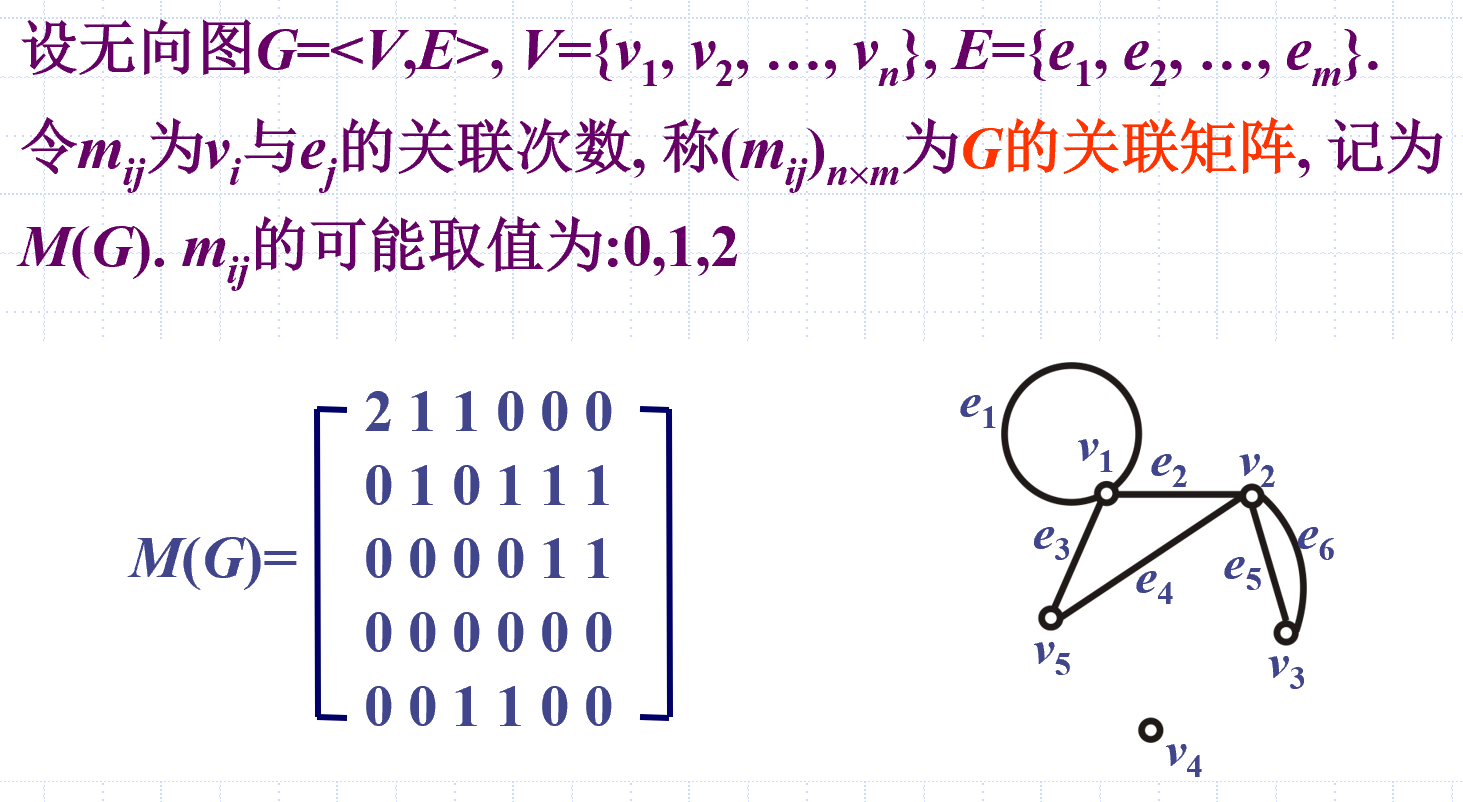
image-20210409161608424
性质
image-20210409162334924

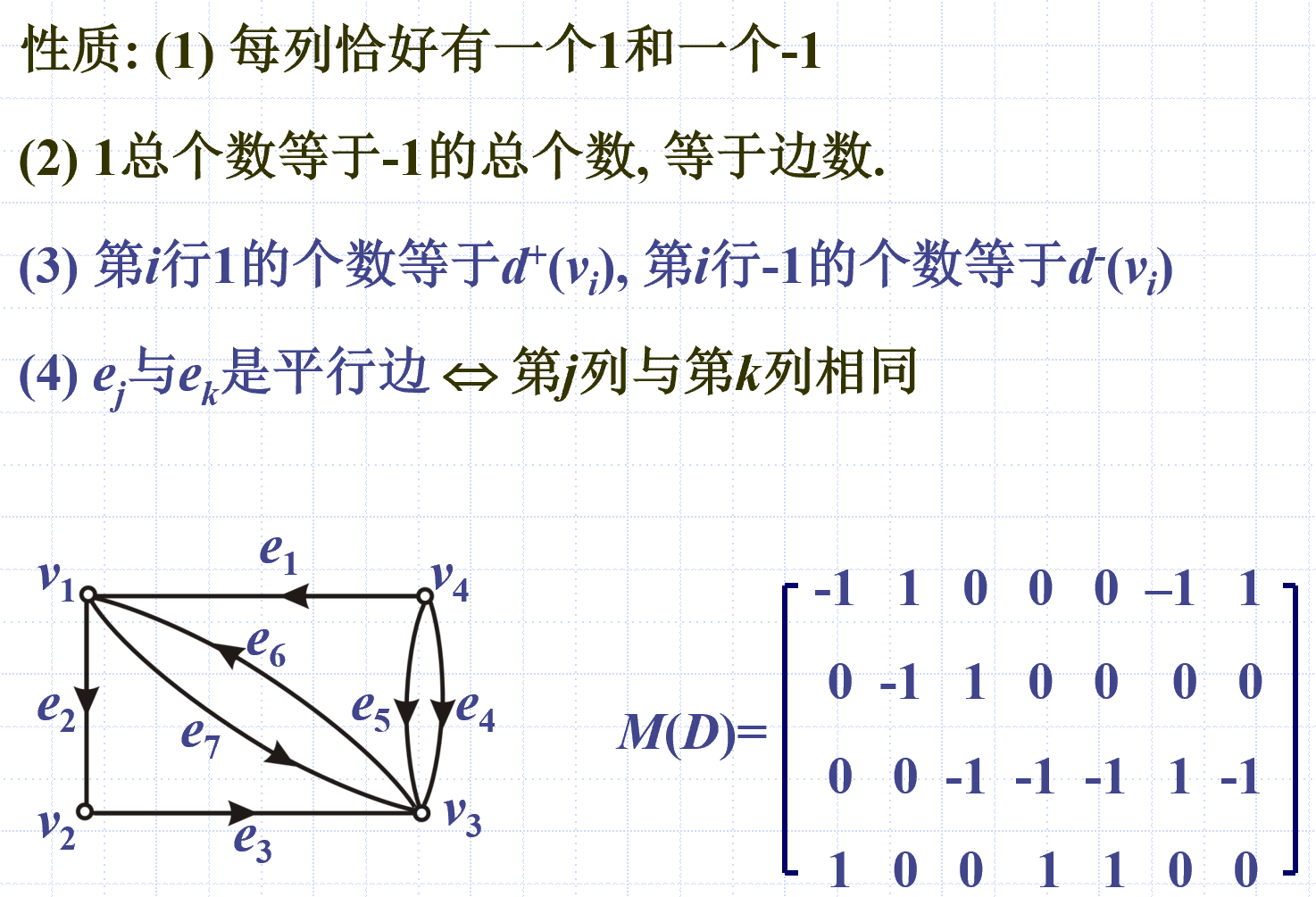
有向无环图的关联矩阵

image-20210409162446867 image-20210409162503071

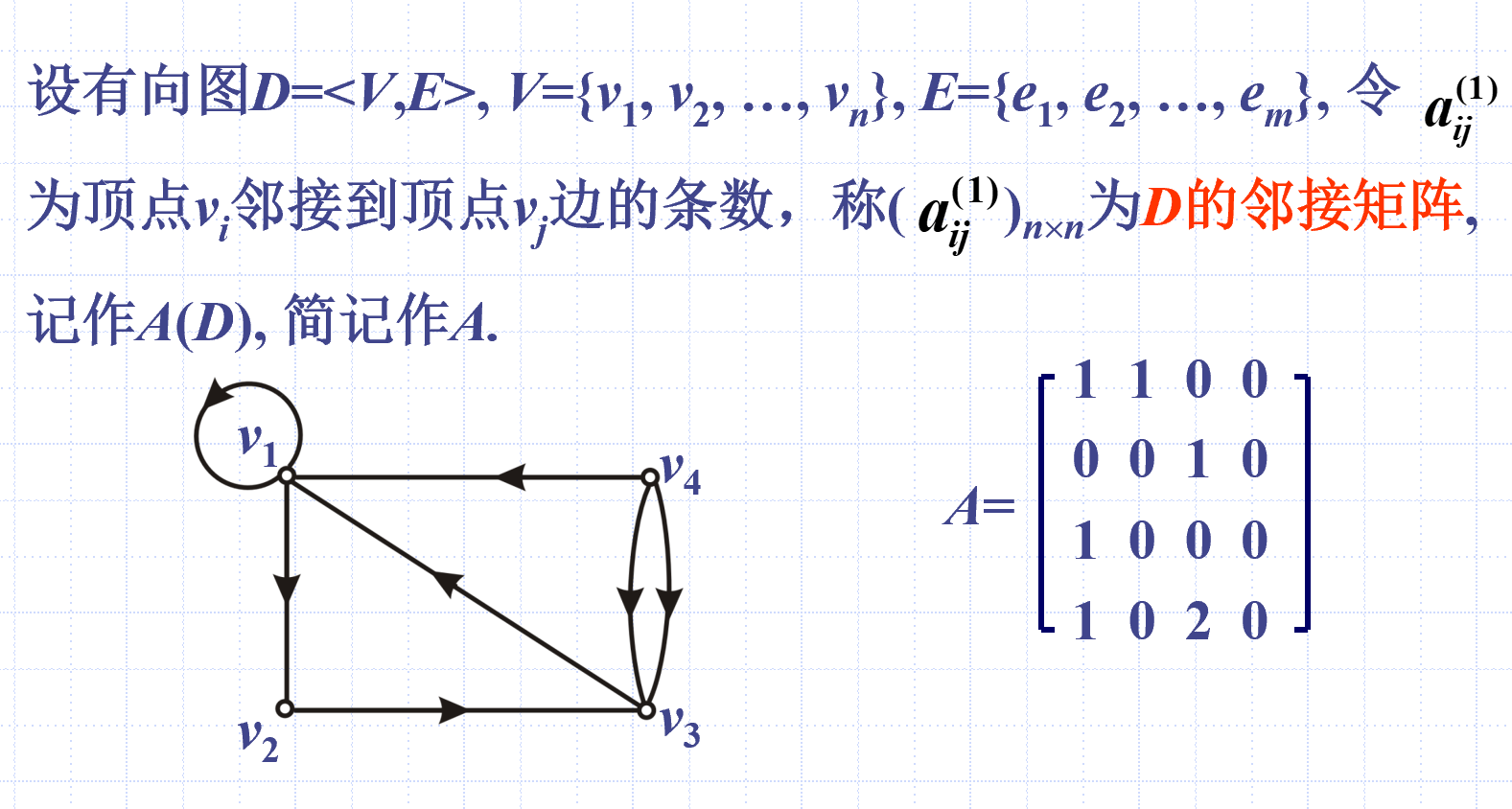
有向图的邻接矩阵

表示点和点的邻接关系

定义
image-20210416141441979
性质
image-20210416141539313
  1. 某顶点的行之和 = 此顶点的出度
  2. 某顶点的列之和 = 此顶点的入度
  3. 总和 = 边数
  4. 对角线和 = 环数
有向图中的通路数与回路数
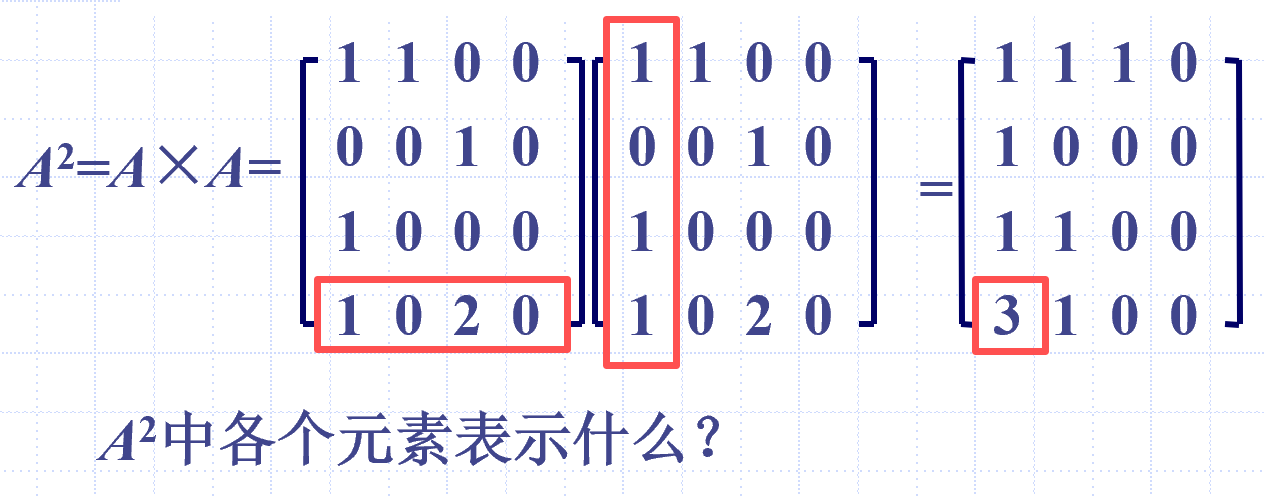
image-20210416142326332

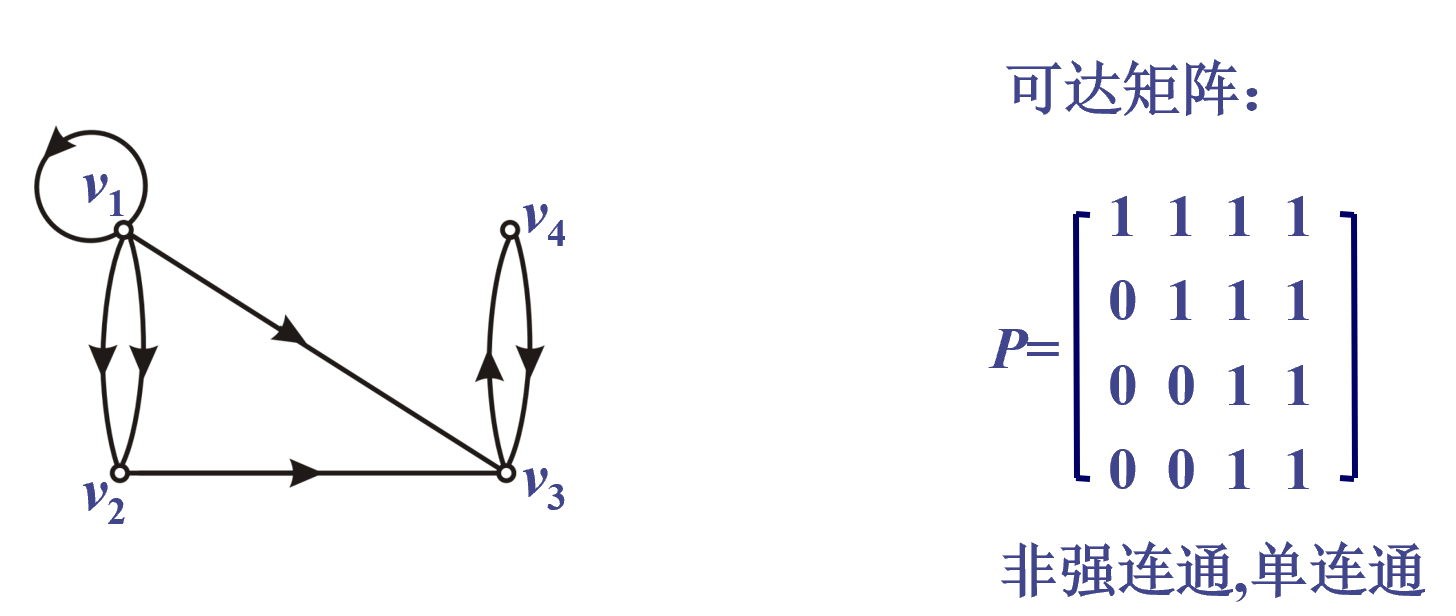
代表 v~4~ 到 v~1~ 有三条长为 2 通路

$a_{ij}^{(n)}$ 表示 v~i~ 到 v~j~ 长为 n 的通路的条数

image-20210416141840323 image-20210416143002658
例
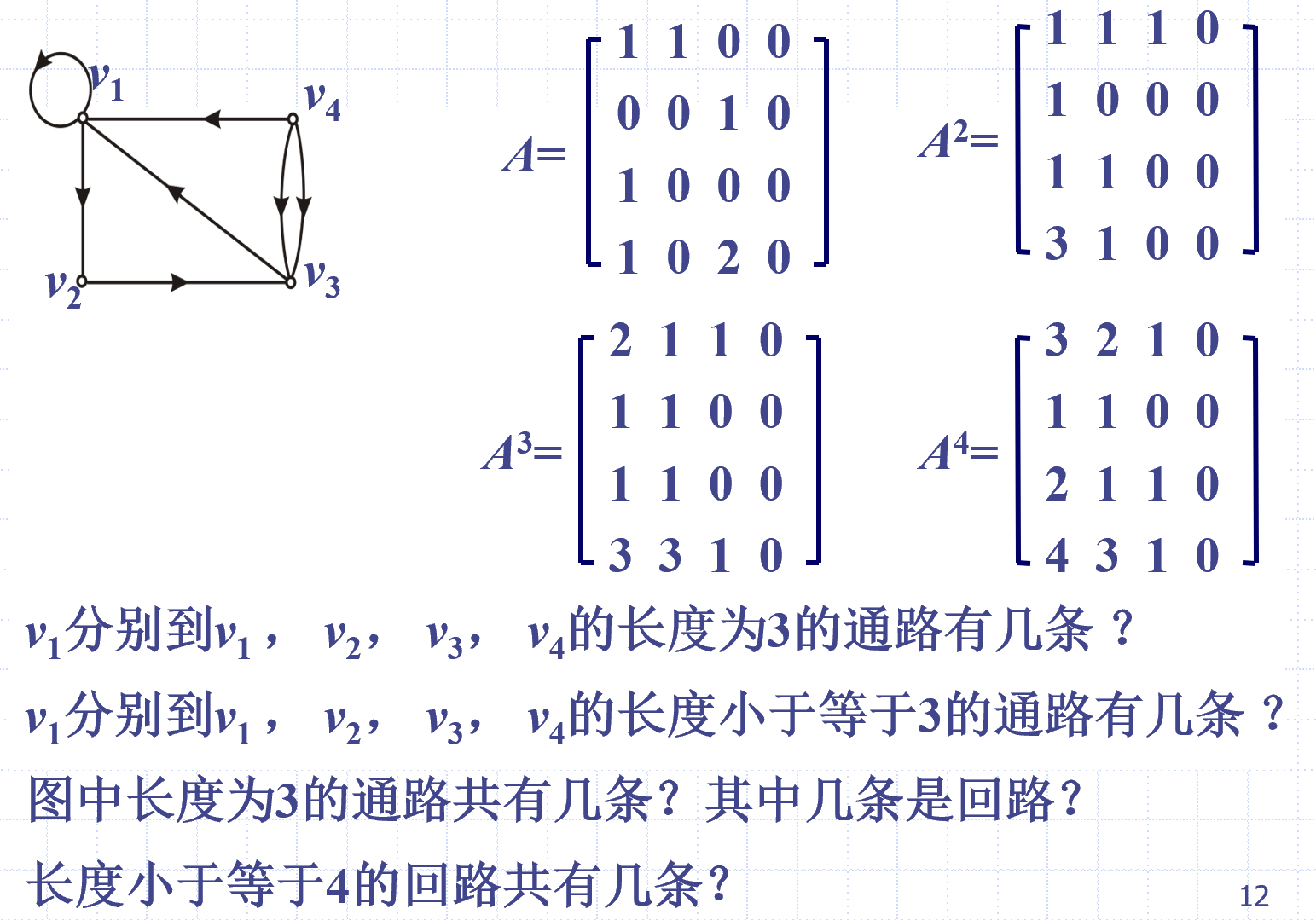
image-20210416143127897
  1. 为 2 1 1 0
  2. 为 4 3 2 0
  3. 有 15 条，3 条回路
  4. 有 10 条

无向图的相邻矩阵

定义
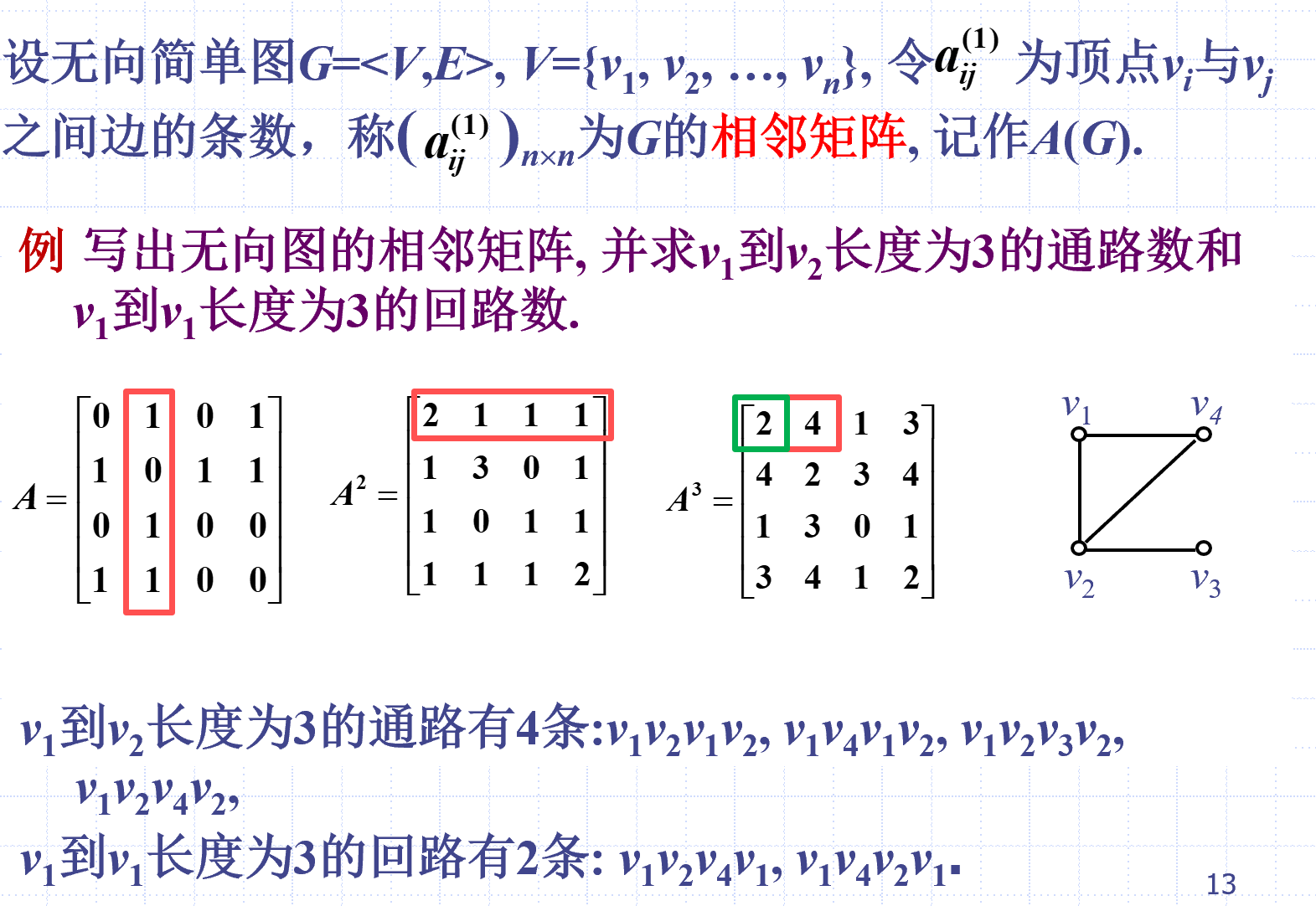
image-20210416143327218

图的可达矩阵

image-20210416143418182

综合例题

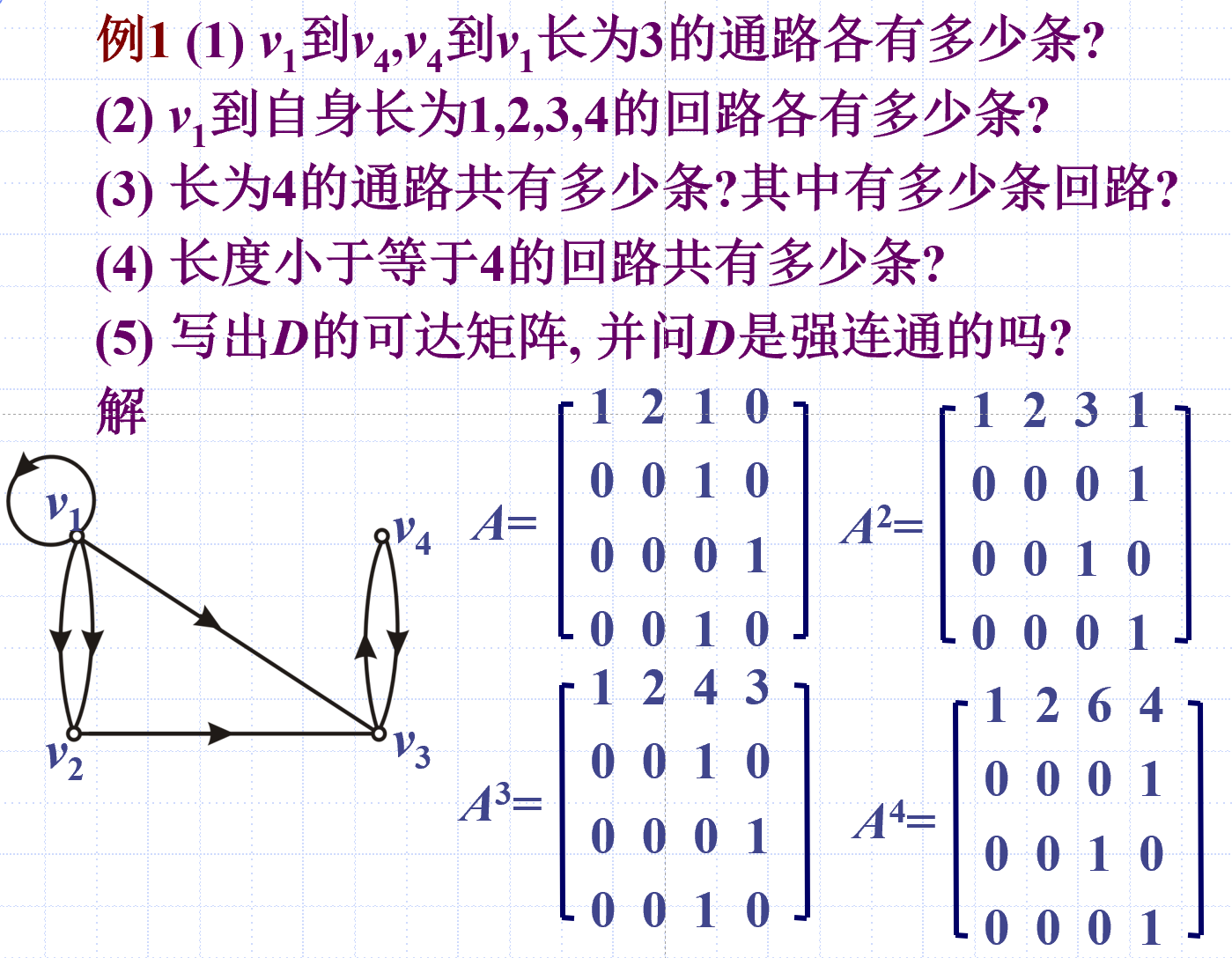
image-20210416143956132 image-20210416144255755 image-20210416144316339

几种特殊的图

二部图

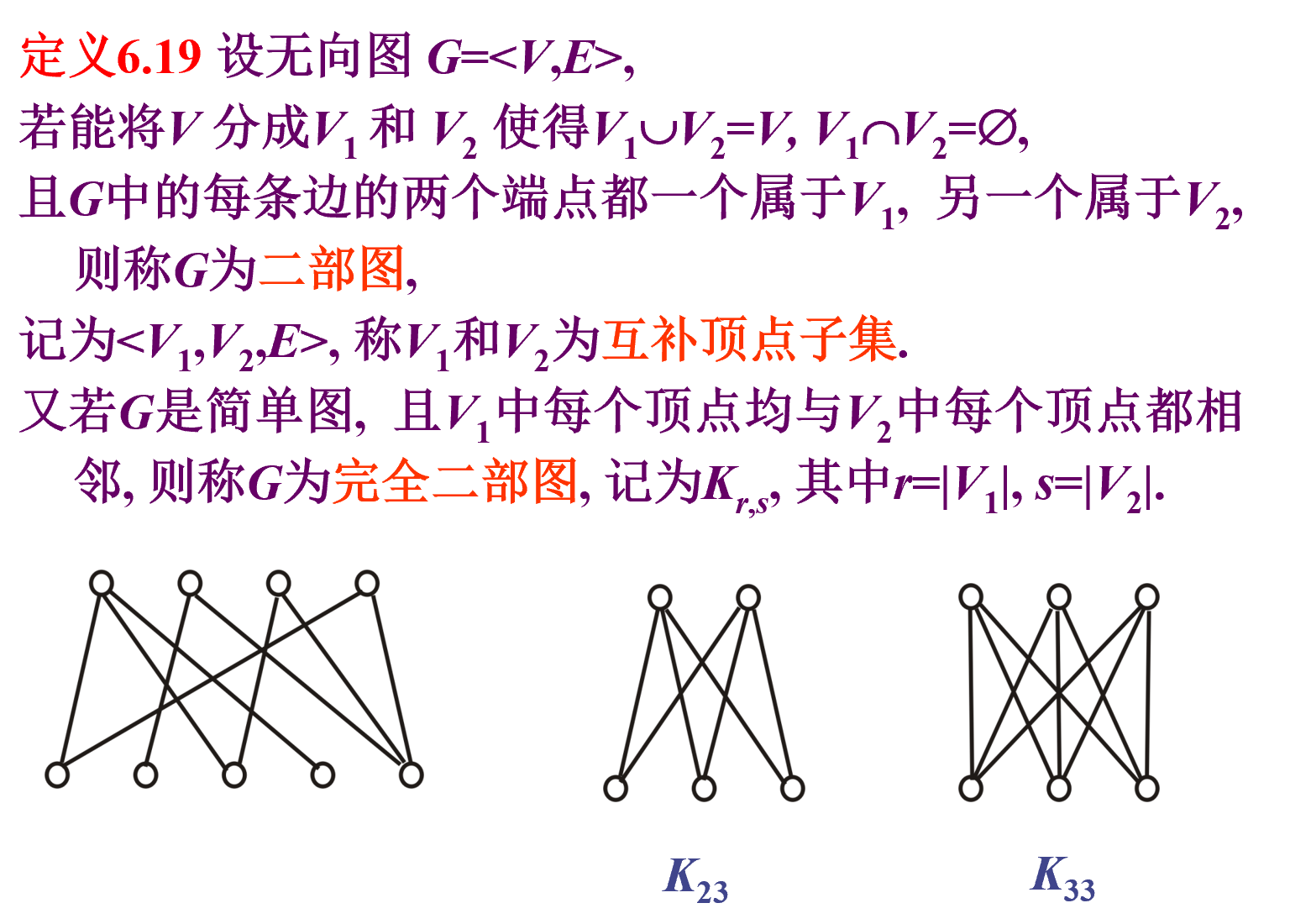
定义

顶点分成两部分，使所有边都从一部分连到另一部分，同一部分内的顶点不能相邻

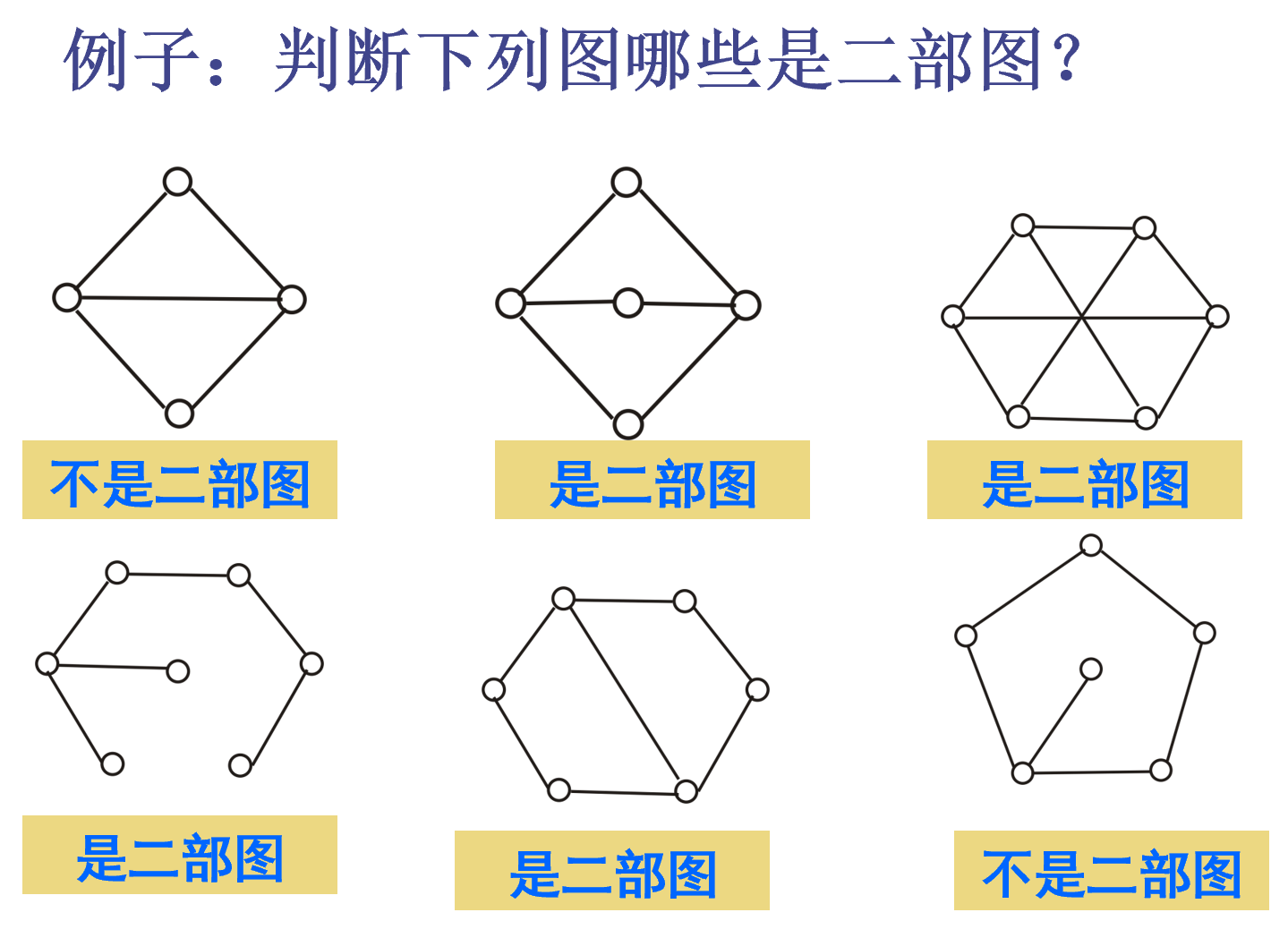
image-20210416145326080 image-20210416150843050
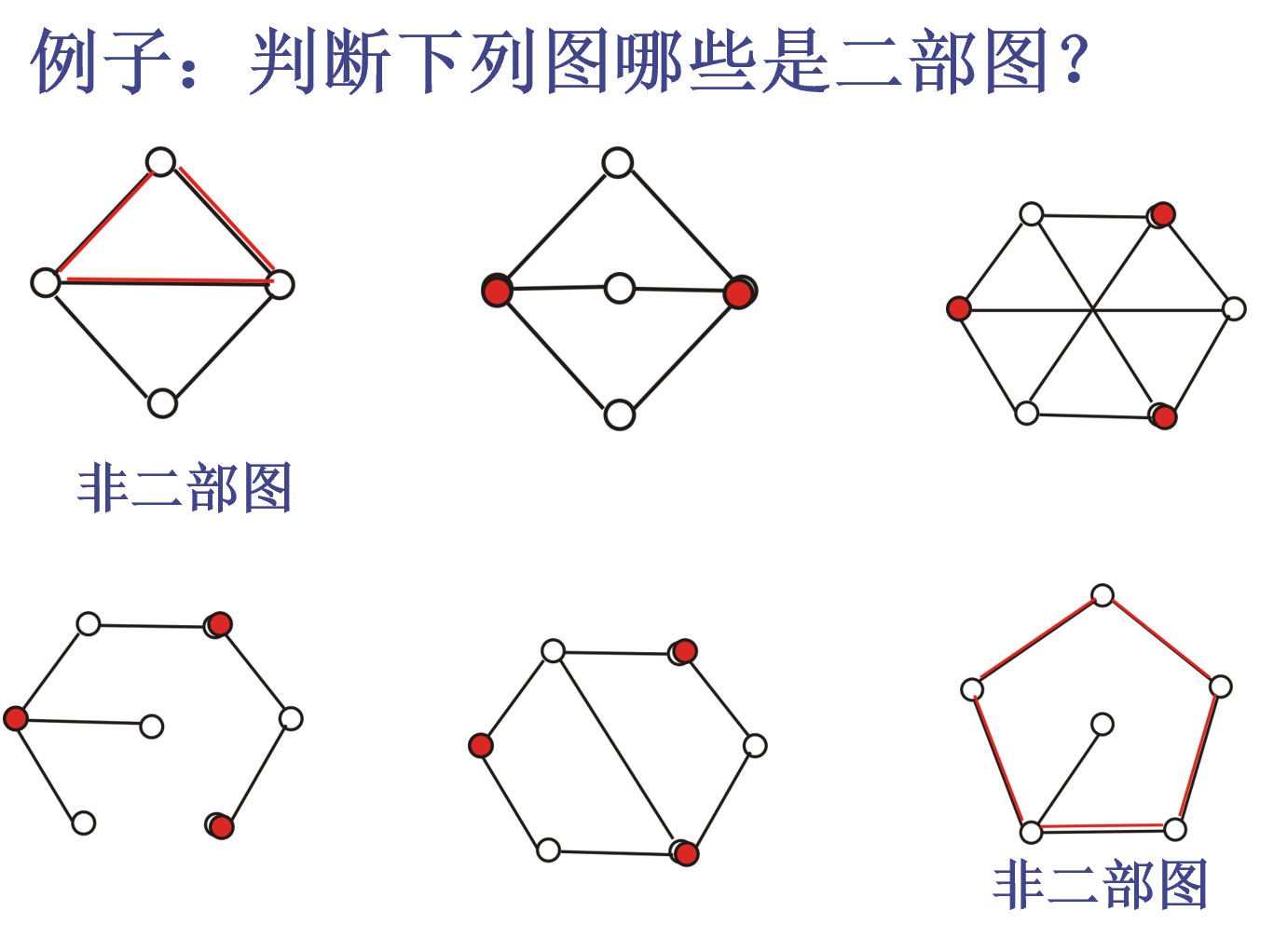
判别定理

二部图当且仅当没有奇长度回路

image-20210416150940780 image-20210416150959779
匹配

匹配：不相邻的边集

极大匹配：不能再加边

最大匹配：边数最多

完备匹配：一边中的点都被连到

完美匹配：所有点都被连到

存在完备匹配的条件

存在完备匹配当且仅当 v~1~ 中任意 k 个顶点至少连接 V~2~ 中 k 个顶点

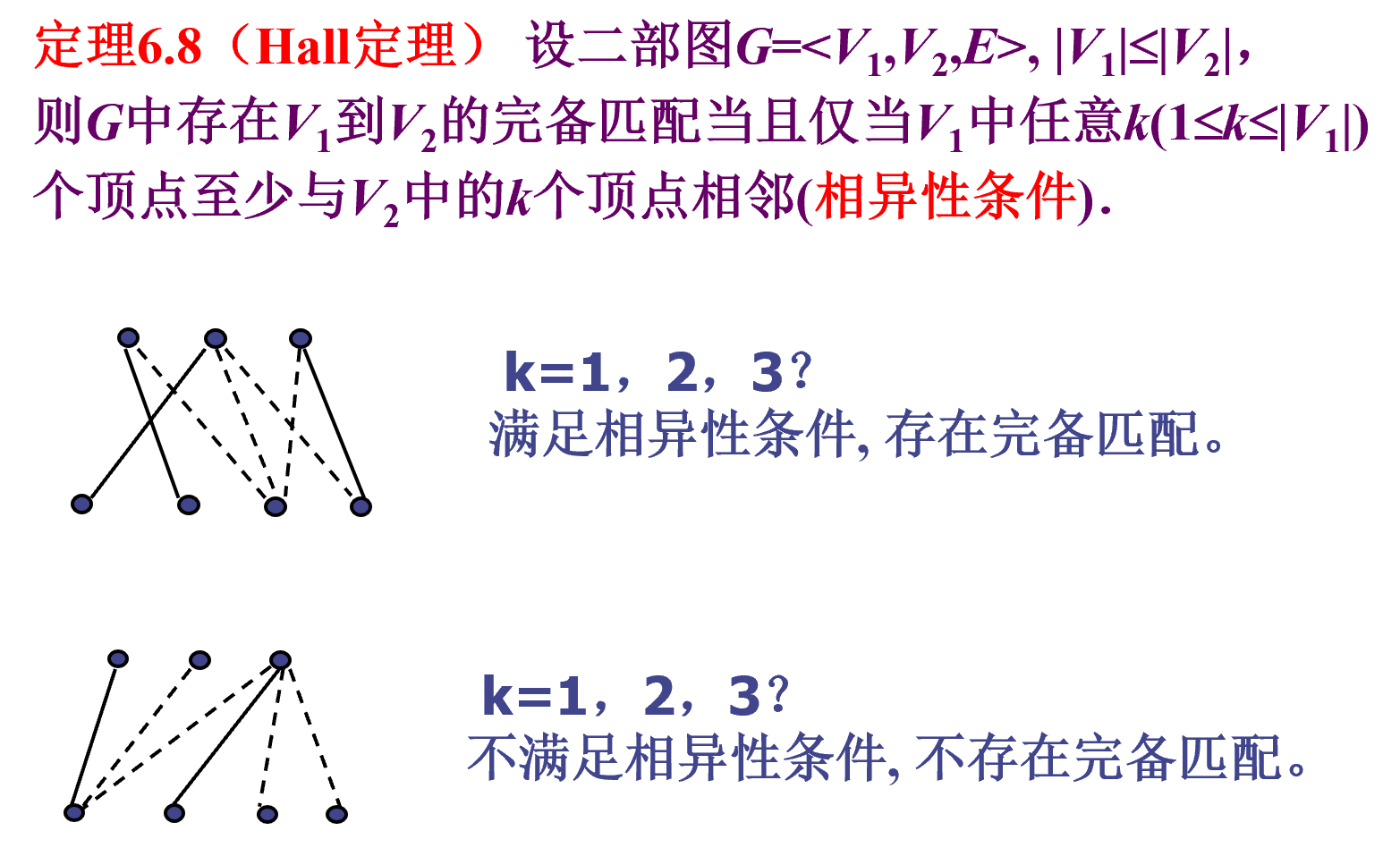
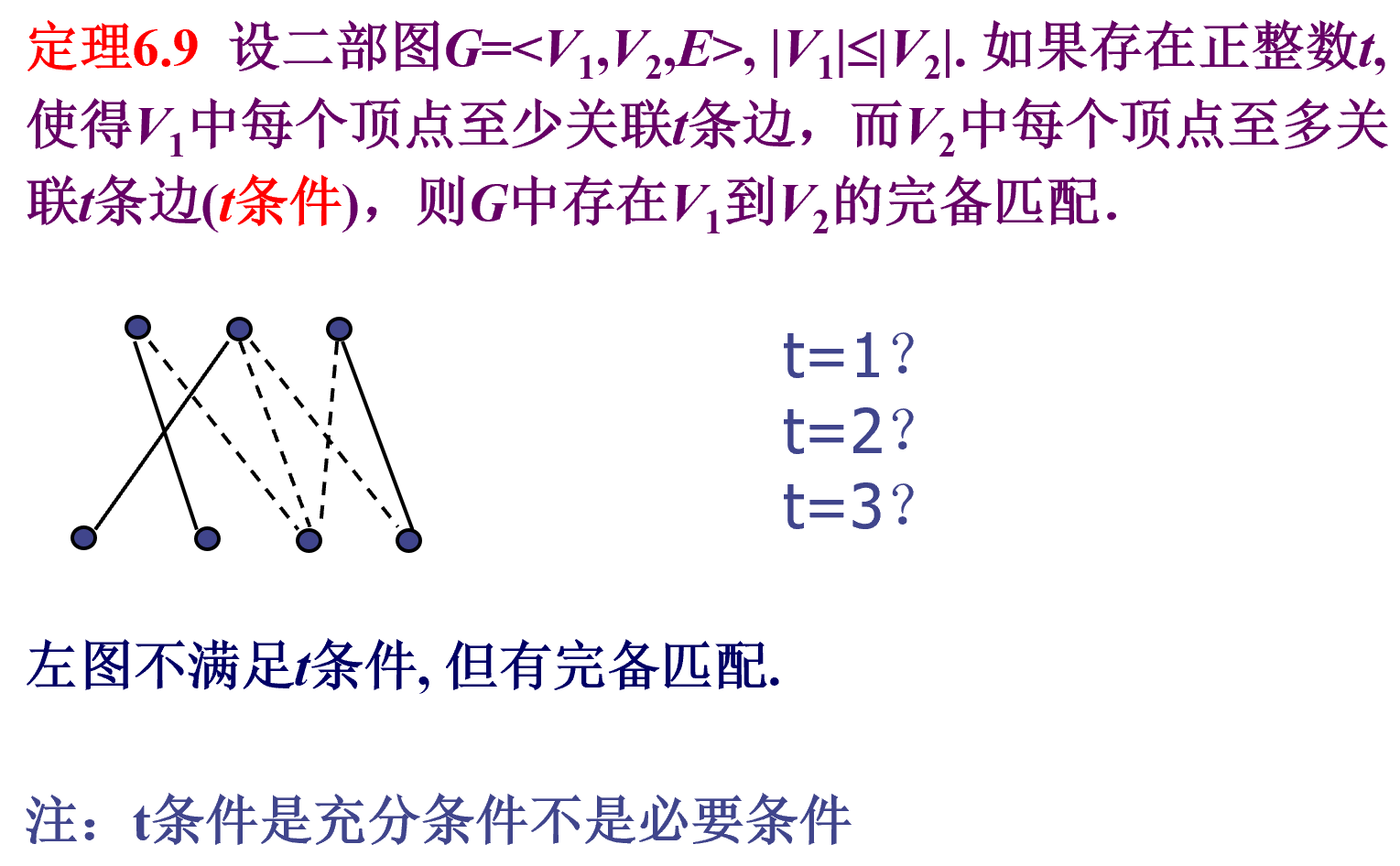
image-20210416151902540 image-20210416151935125
例
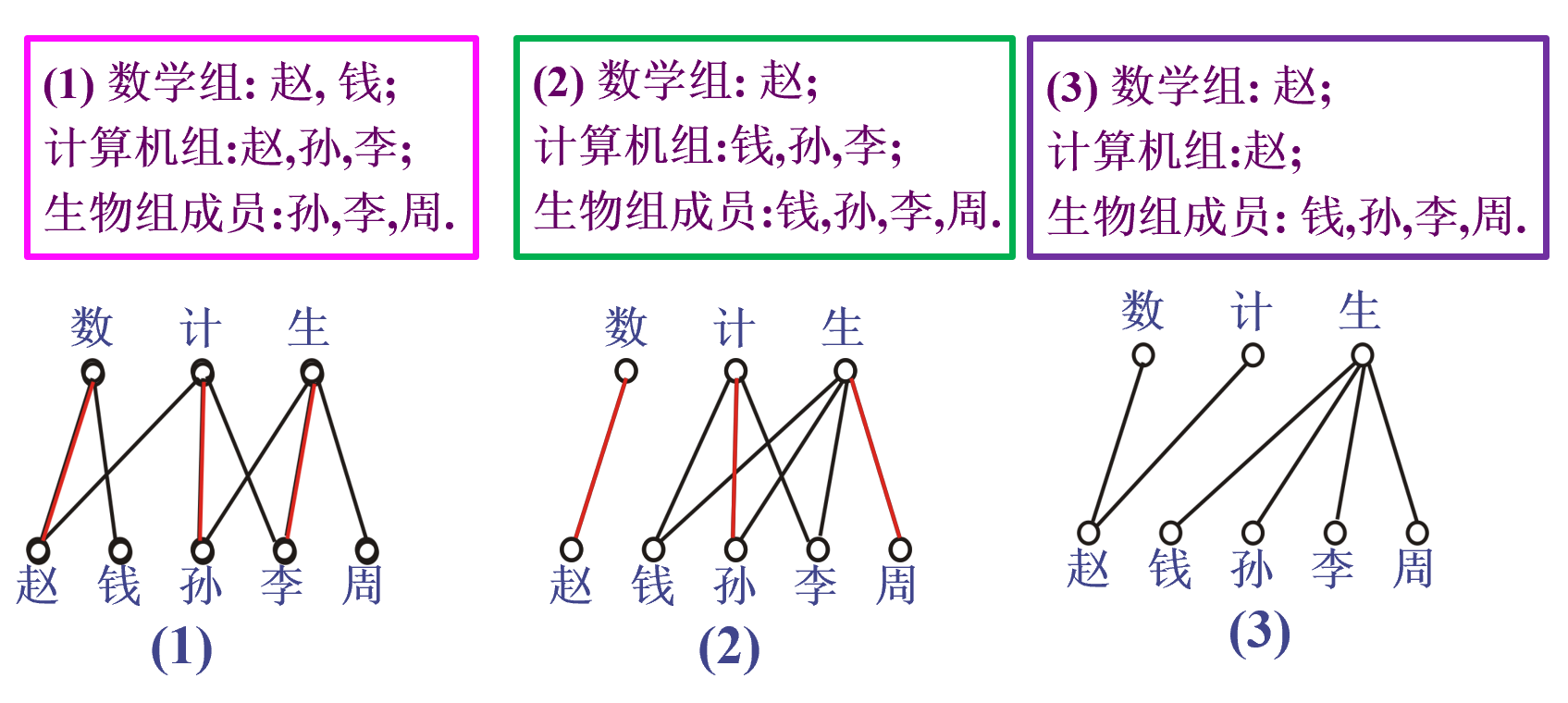
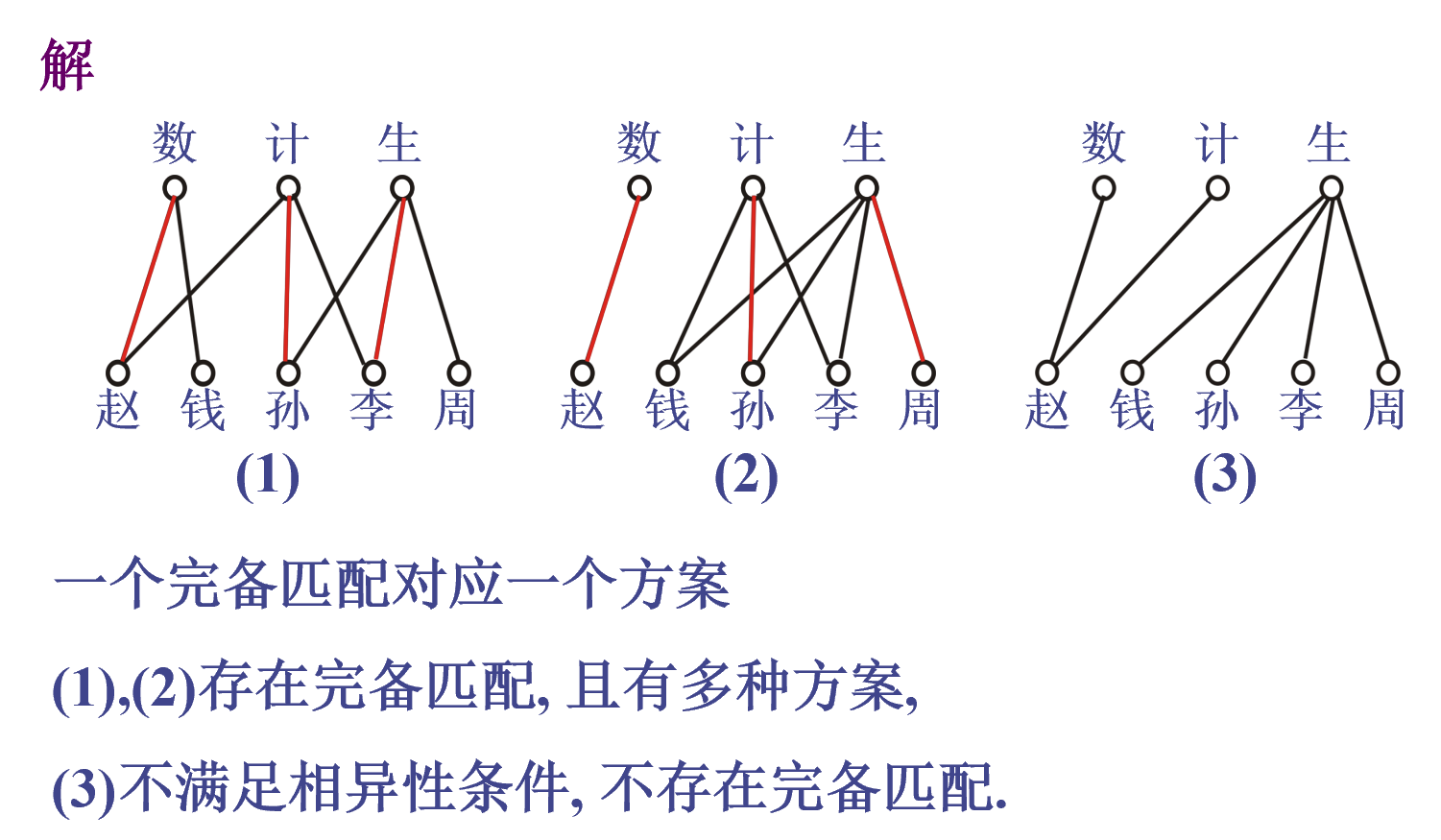
image-20210416152114182 image-20210416152157235 image-20210416152213067

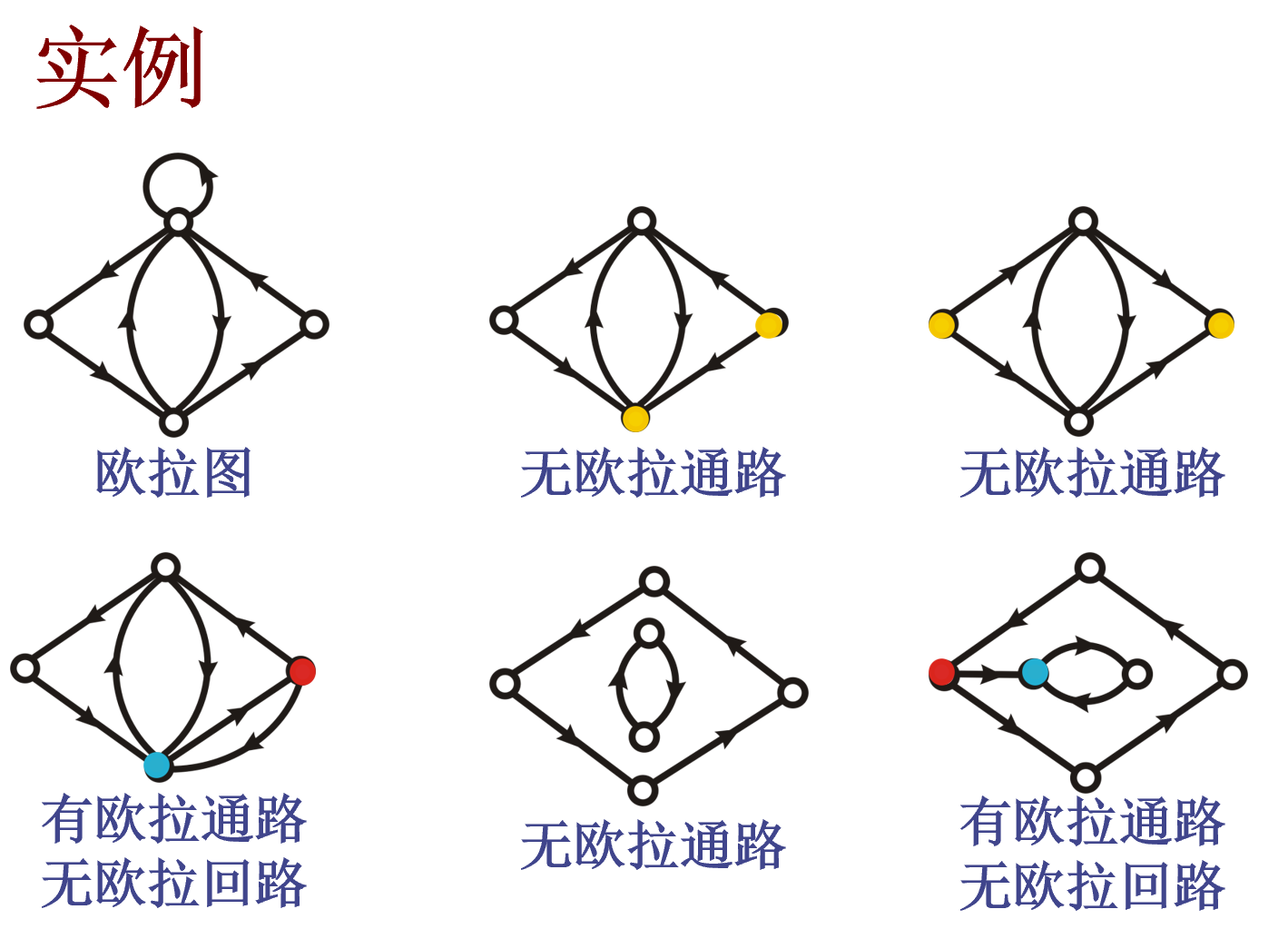
欧拉图

一笔画，简单通路（回路）

存在 “经过所有顶点、每条边恰好经过一次” 的回路

定义
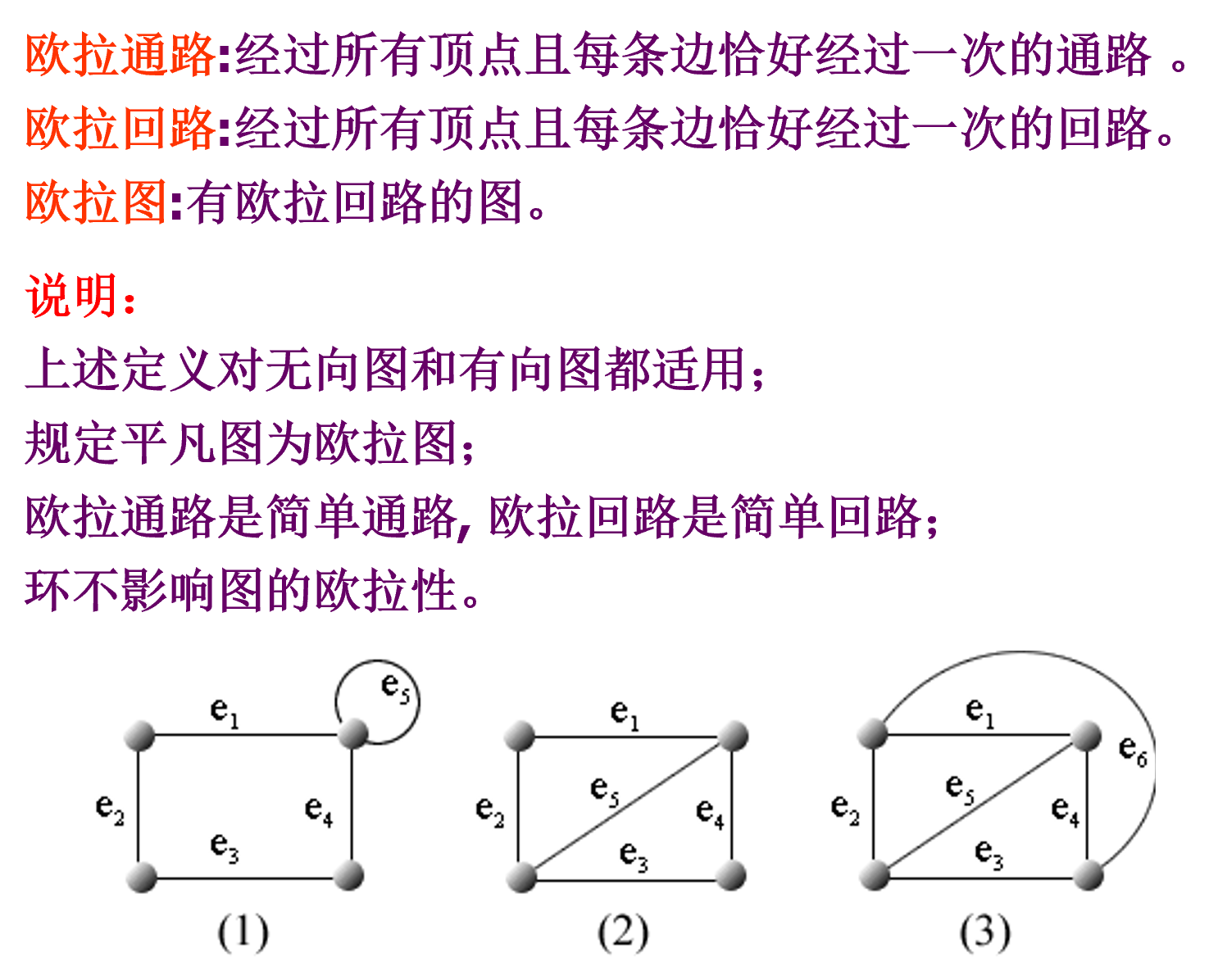
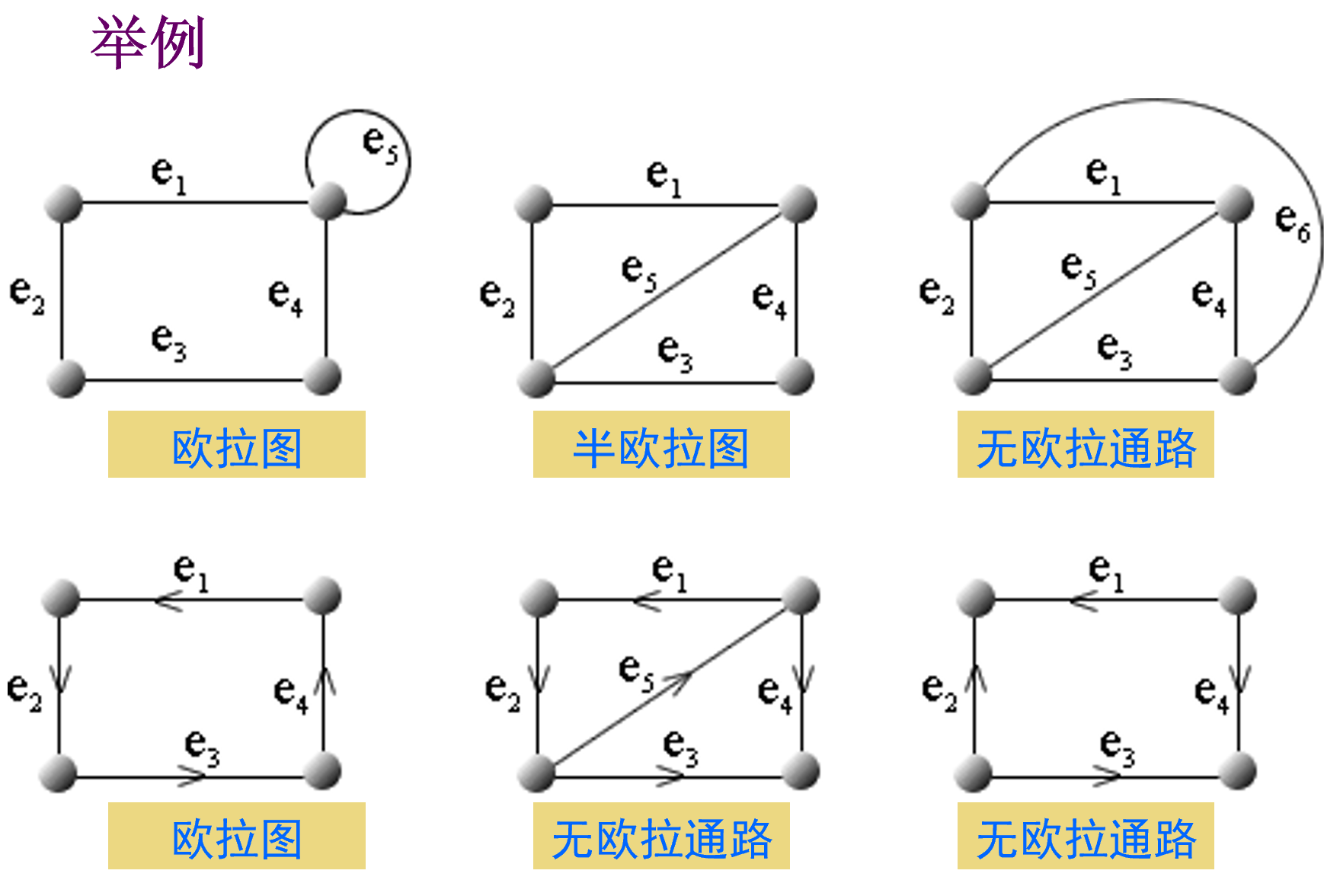
image-20210416152647951 image-20210416152939601
无向欧拉图判别定理

无奇度顶点的连通图

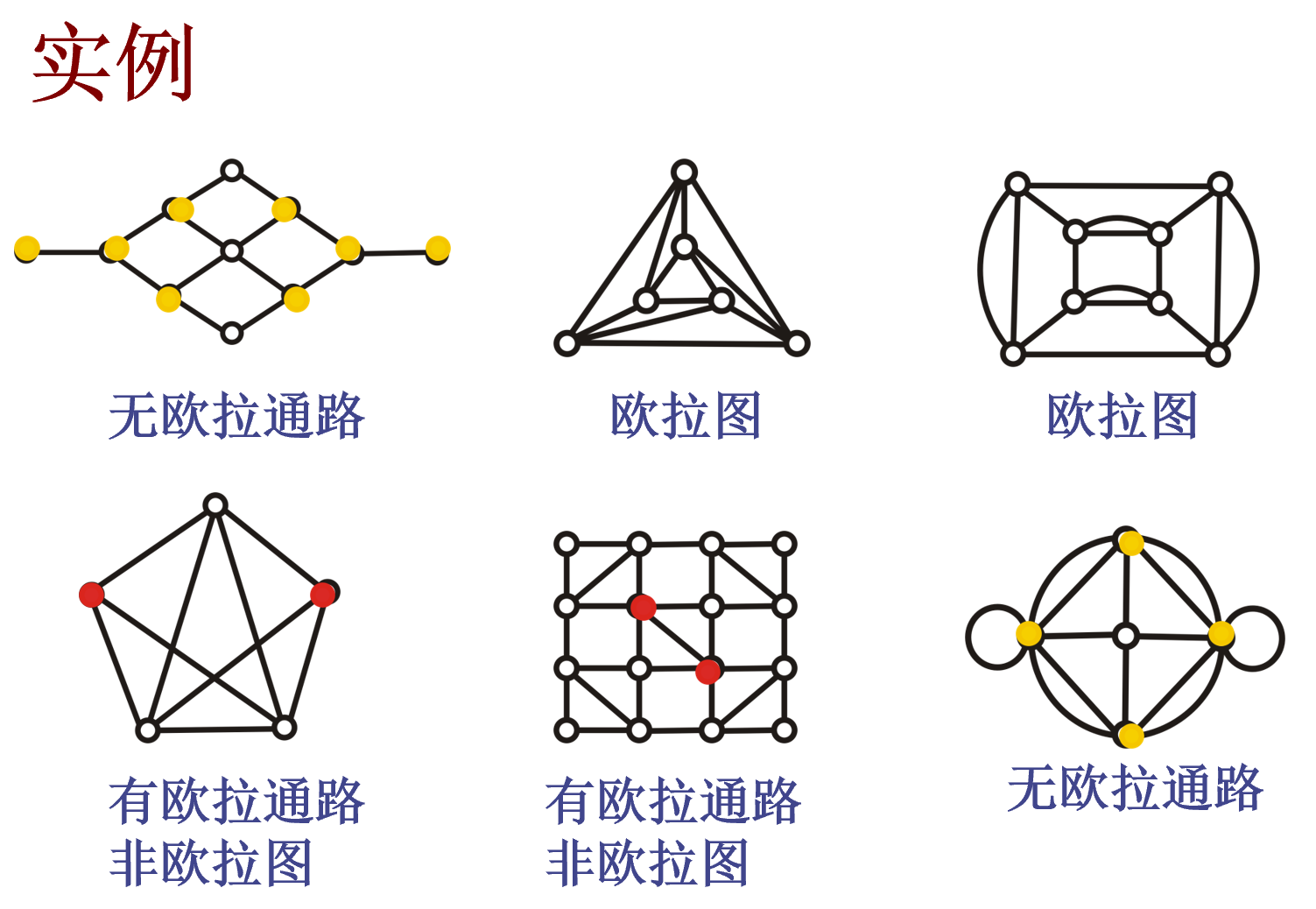
image-20210416160328920 image-20210416160221755 image-20210416160408115
有向欧拉图判别定理

所有顶点的入读等于出度的连通图

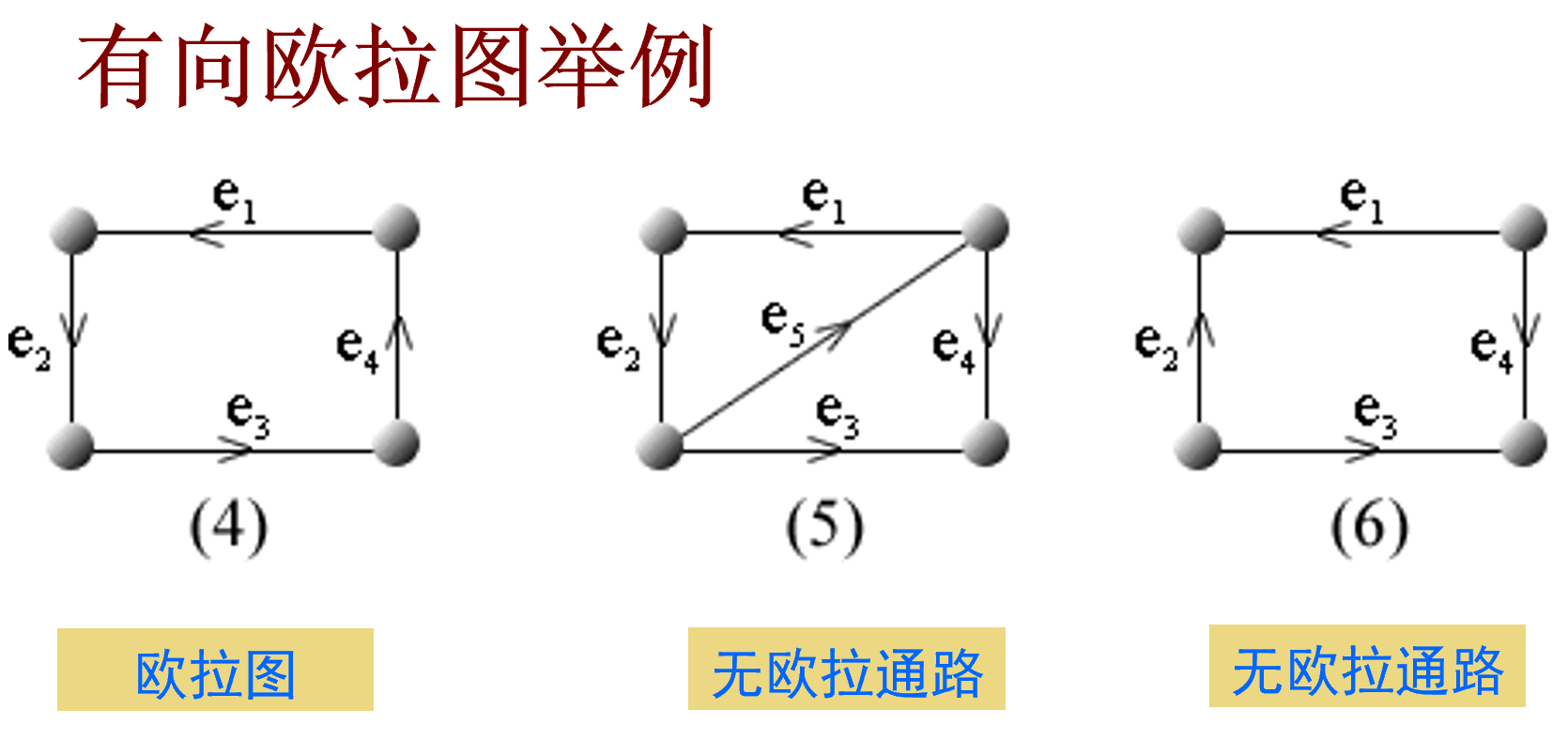
image-20210416160453655 image-20210416160649631 image-20210416160705582
求欧拉图中欧拉回路的算法

==能不走桥就不走桥==

image-20210416161739665
例
image-20210416161940828

哈密顿图

找哈密顿图的技巧

找出二度点，列出必经之路，连接

定义

存在 “每个点经过且只经过一次” 的回路

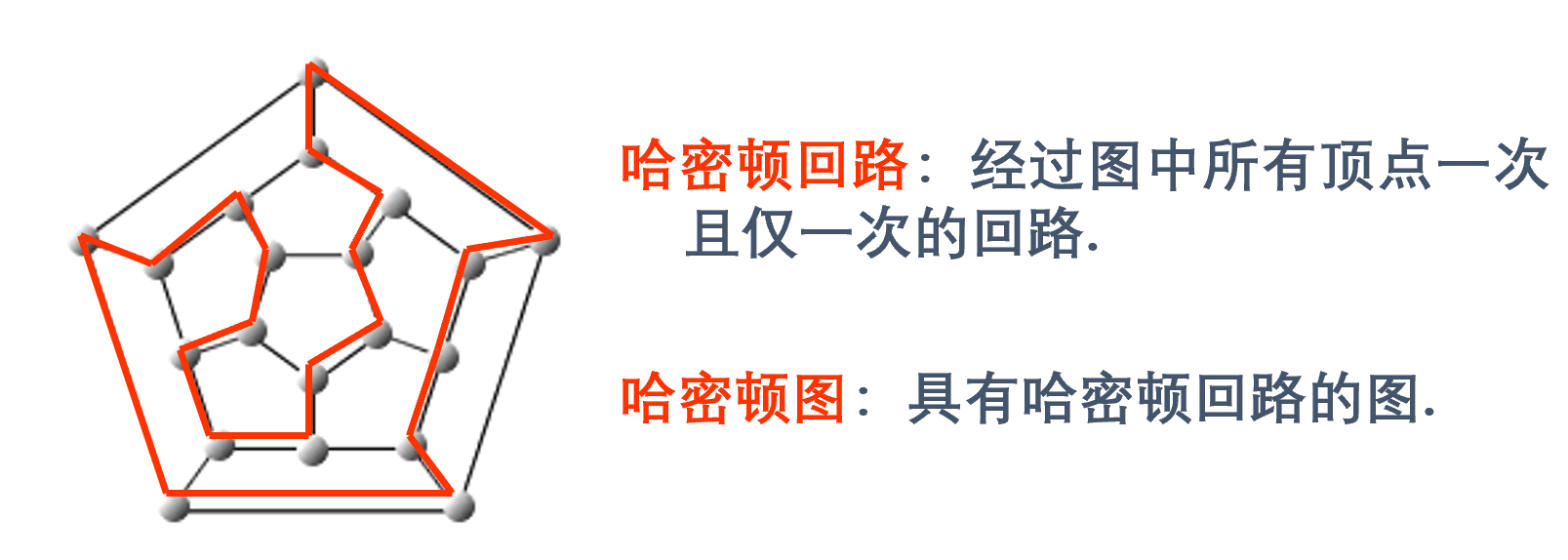
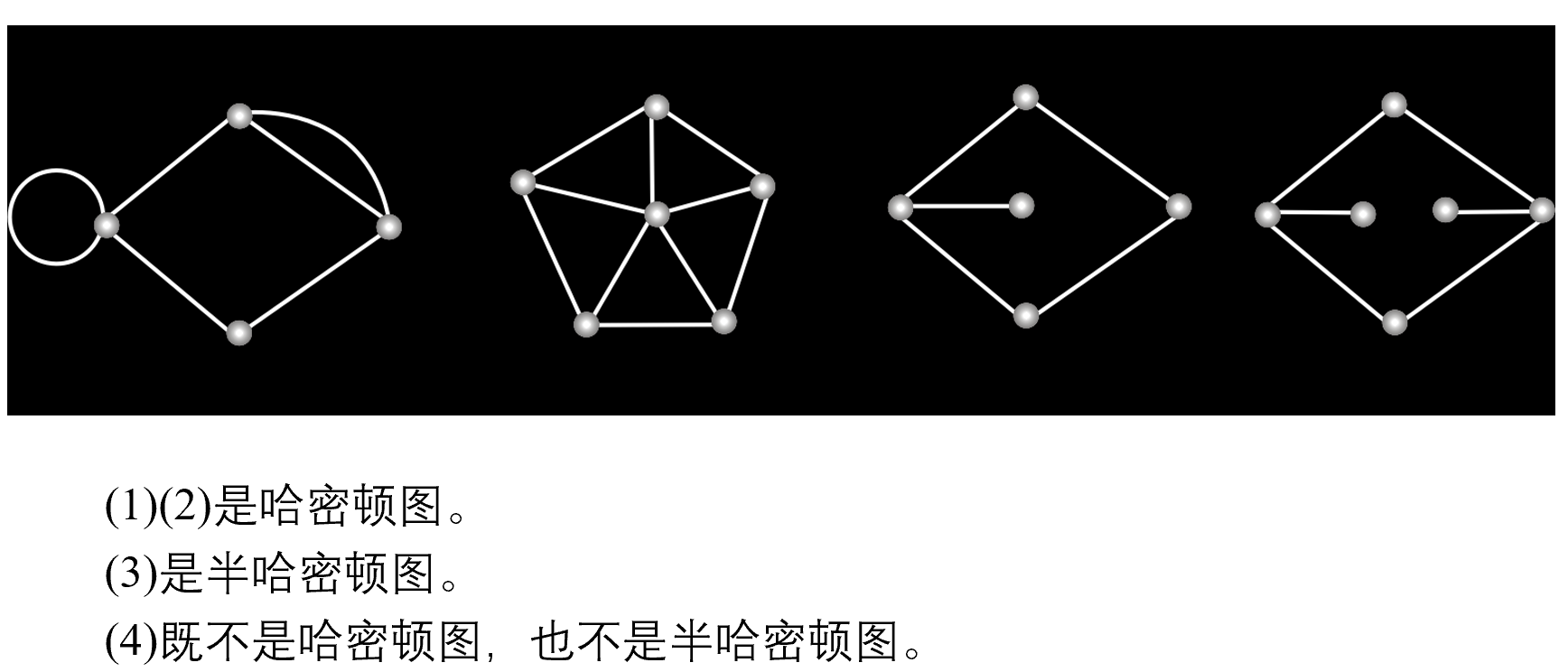
image-20210423141534075 image-20210423141847450
必要条件
定理 6.12

用逆否命题可以证伪，不可以证真

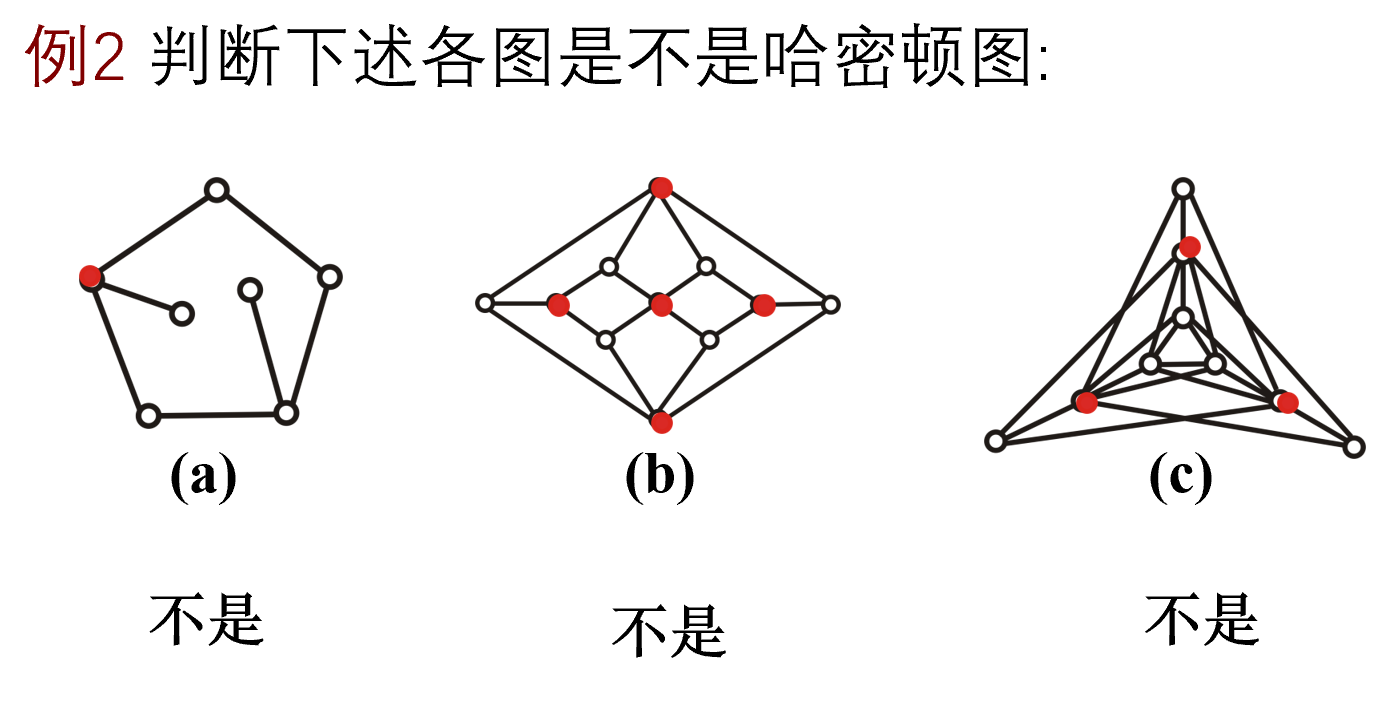
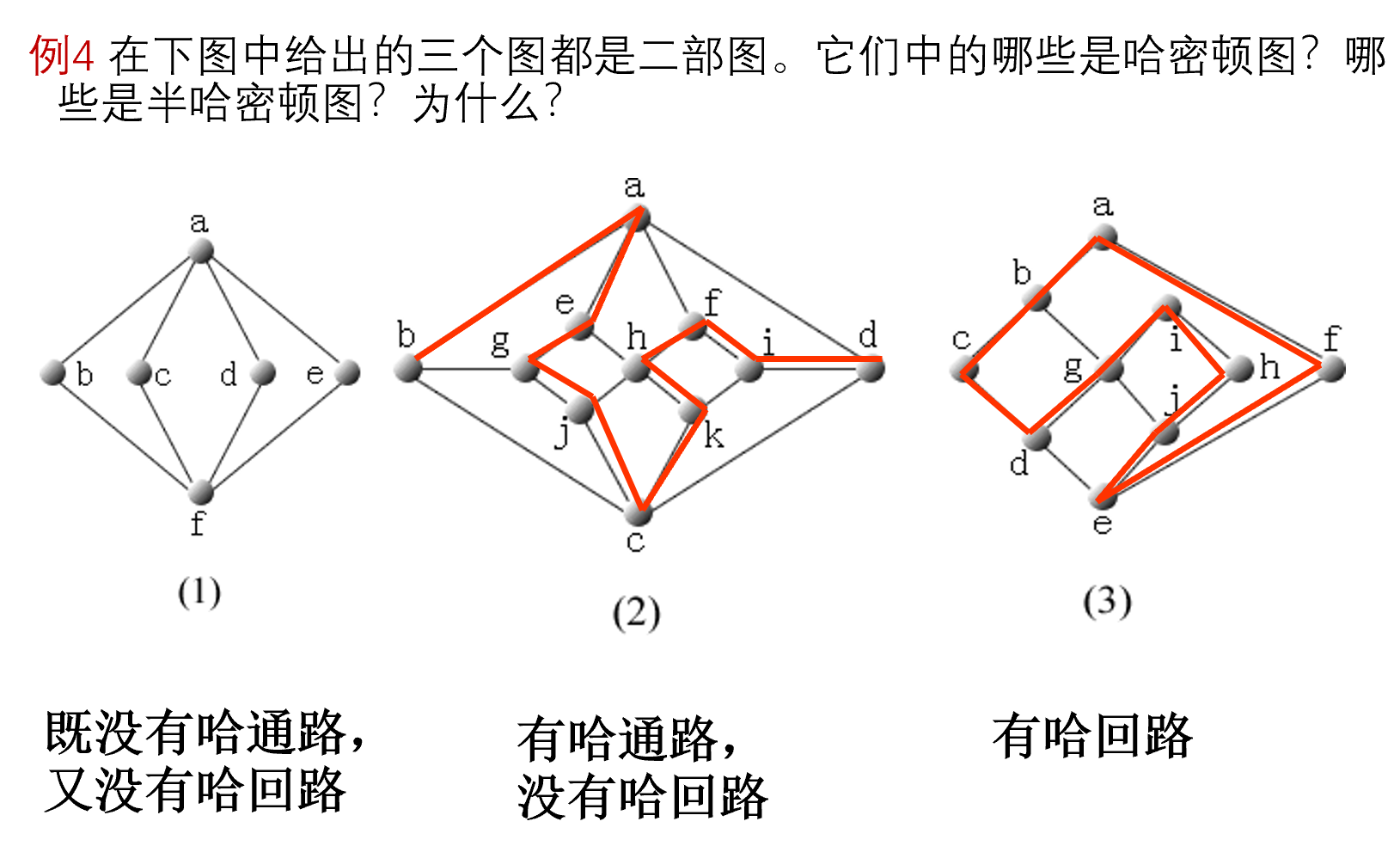
image-20210423142626081 image-20210423142640733 image-20210423142657886 image-20210423142847917
另一种必要条件
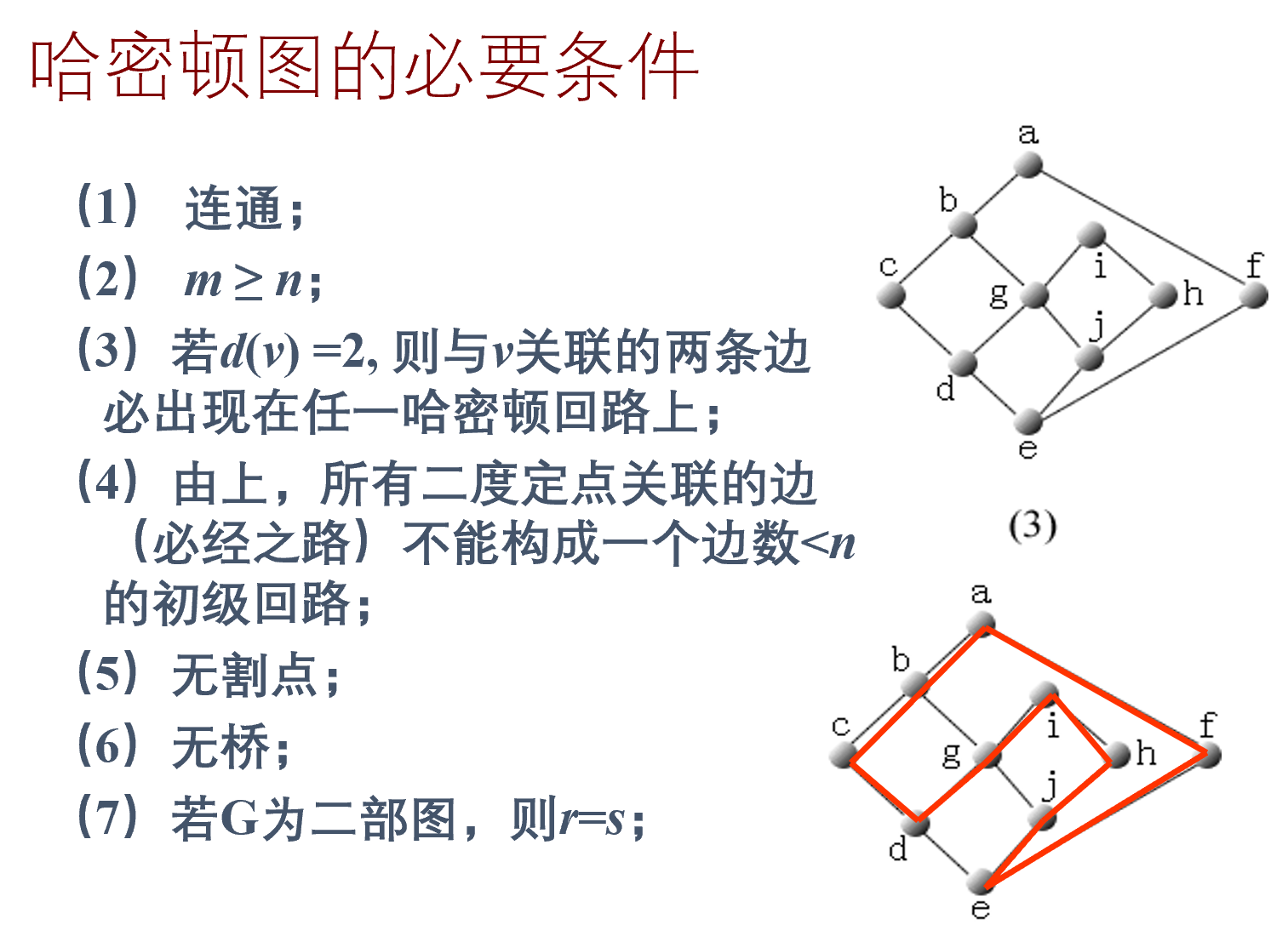
image-20210423143047847

二部图（r 和 s）

  • 个数差一，通路；

  • 个数相同，回路；

  • 个数差二以上，没有路

充分条件

任意两个不相邻点度数和大于等于 n

可以证真，不可证伪

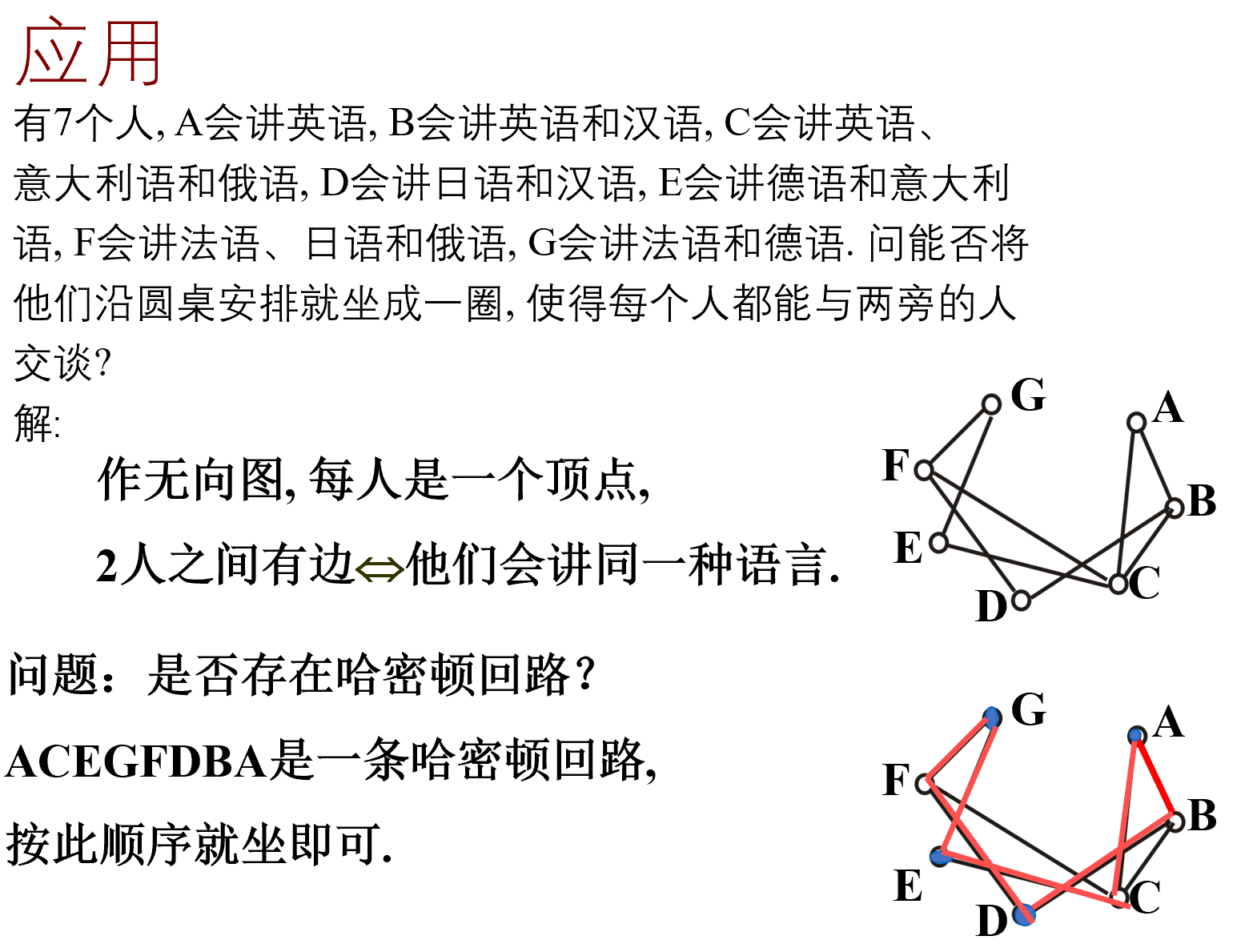
image-20210423143927758 image-20210423143949418
欧拉图与哈密顿图的判别方法

http://markdown-1303167219.cos.ap-shanghai.myqcloud.com/image-20210423152453661.png

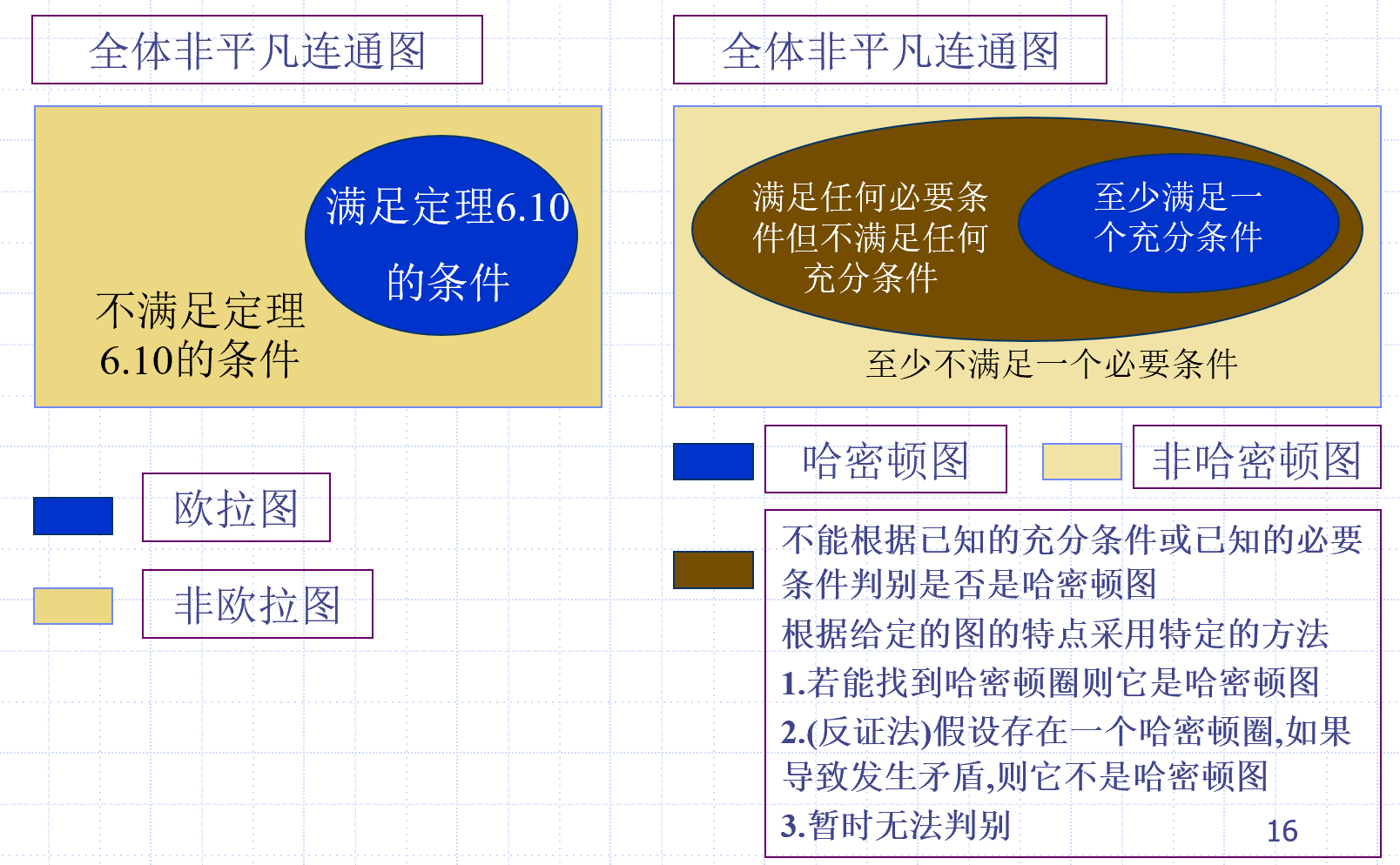
平面图

定义

平面图与平面嵌入

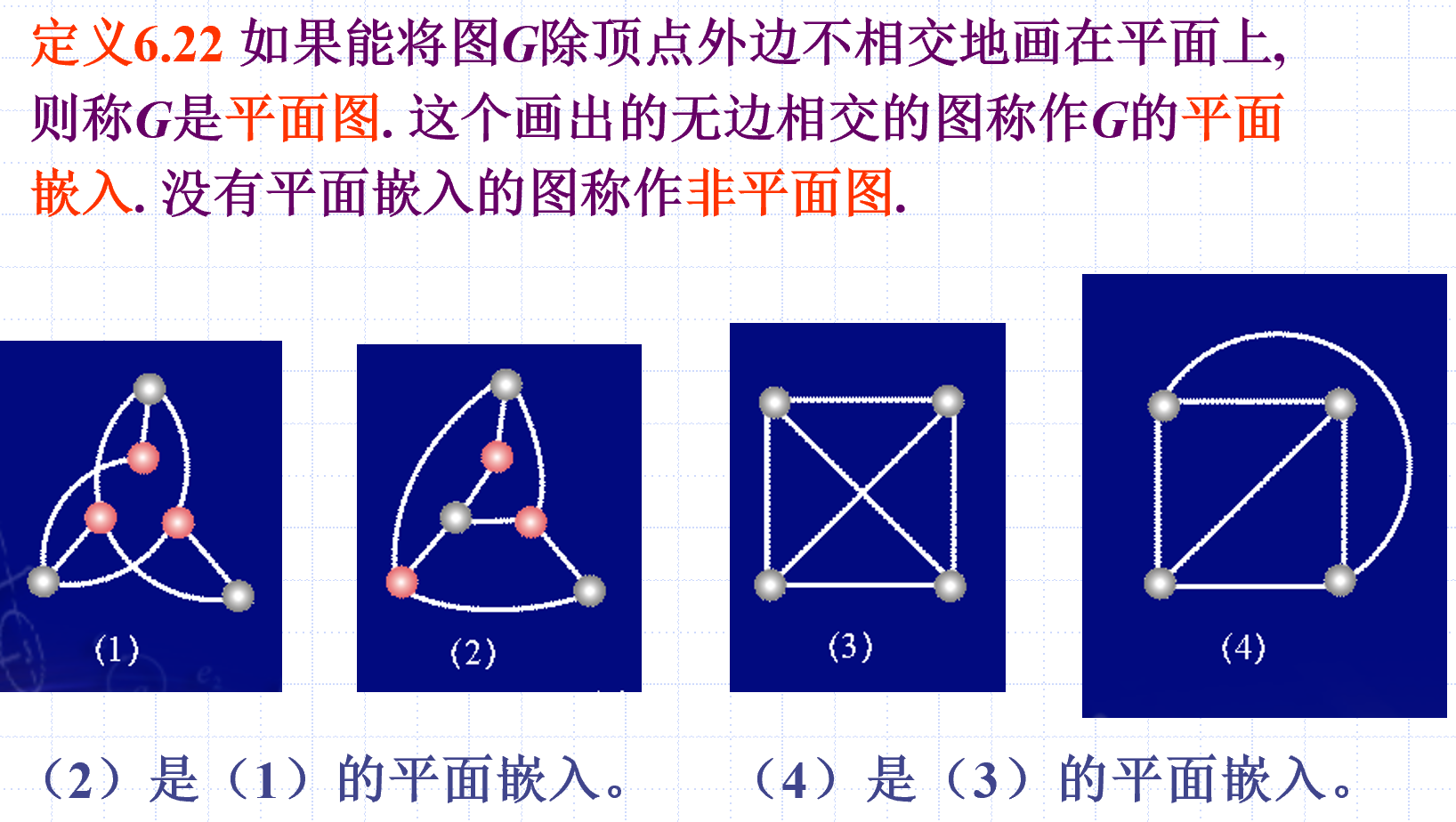
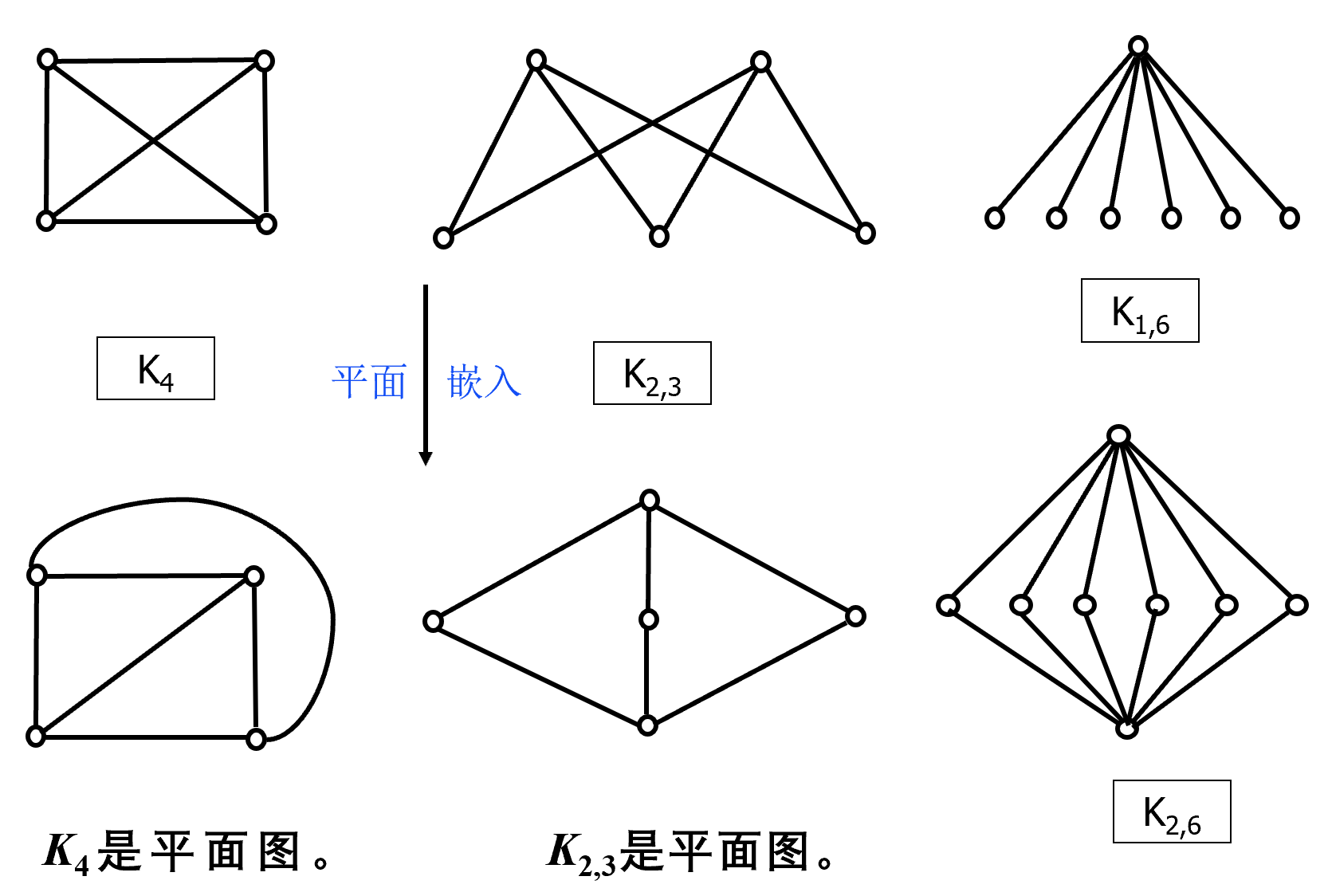
image-20210423152913638 image-20210423153027125 image-20210423153104960 image-20210423153334071
平面图的面及其次数
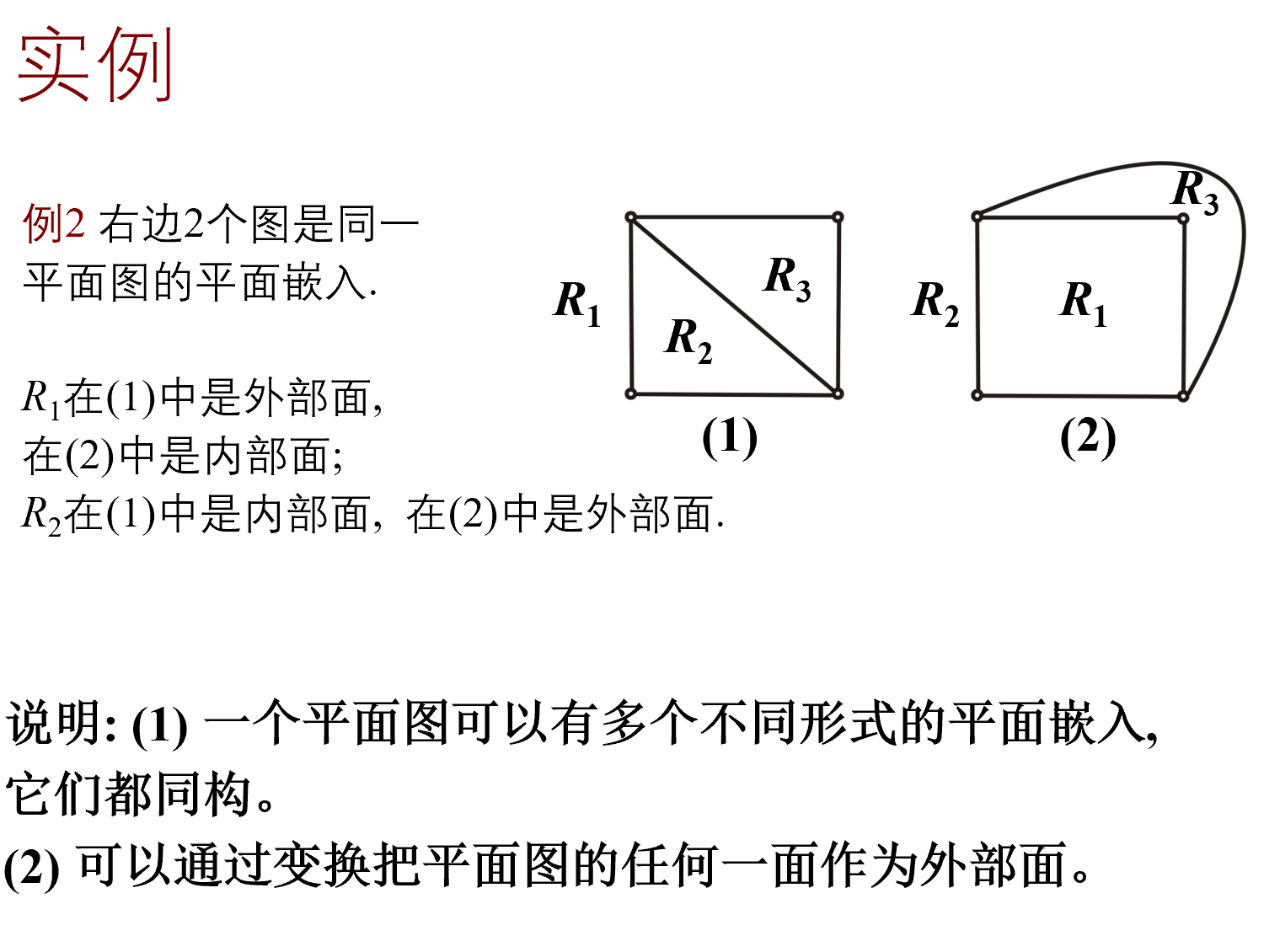
image-20210423153940410 image-20210423153729059

面次和定理

image-20210423154744548
极大平面图

不能加平行边，因为基于简单图

概念

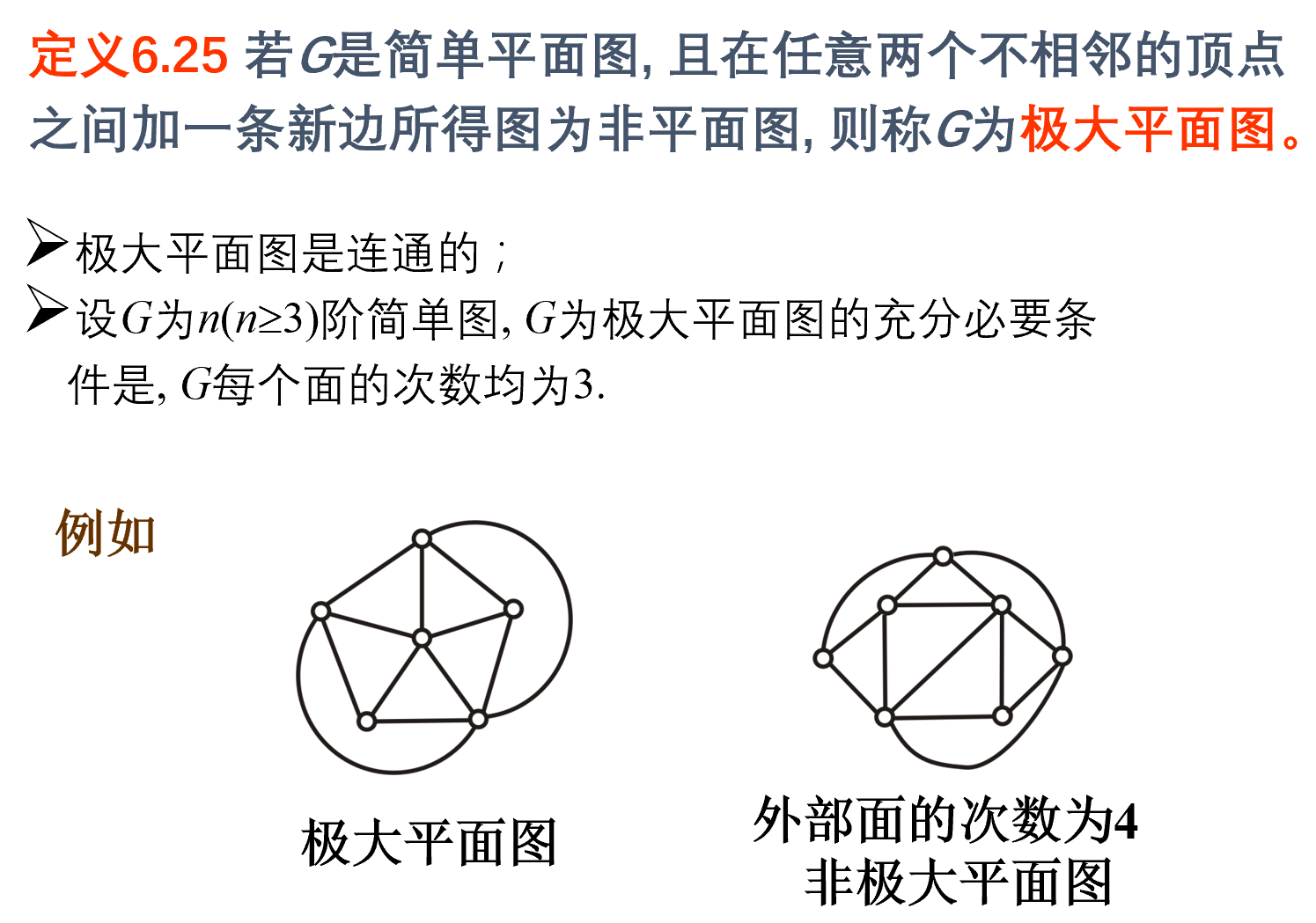
充要条件：每个面的次数都是 3

故，次数是 4 可以加边，次数是 3 加不了

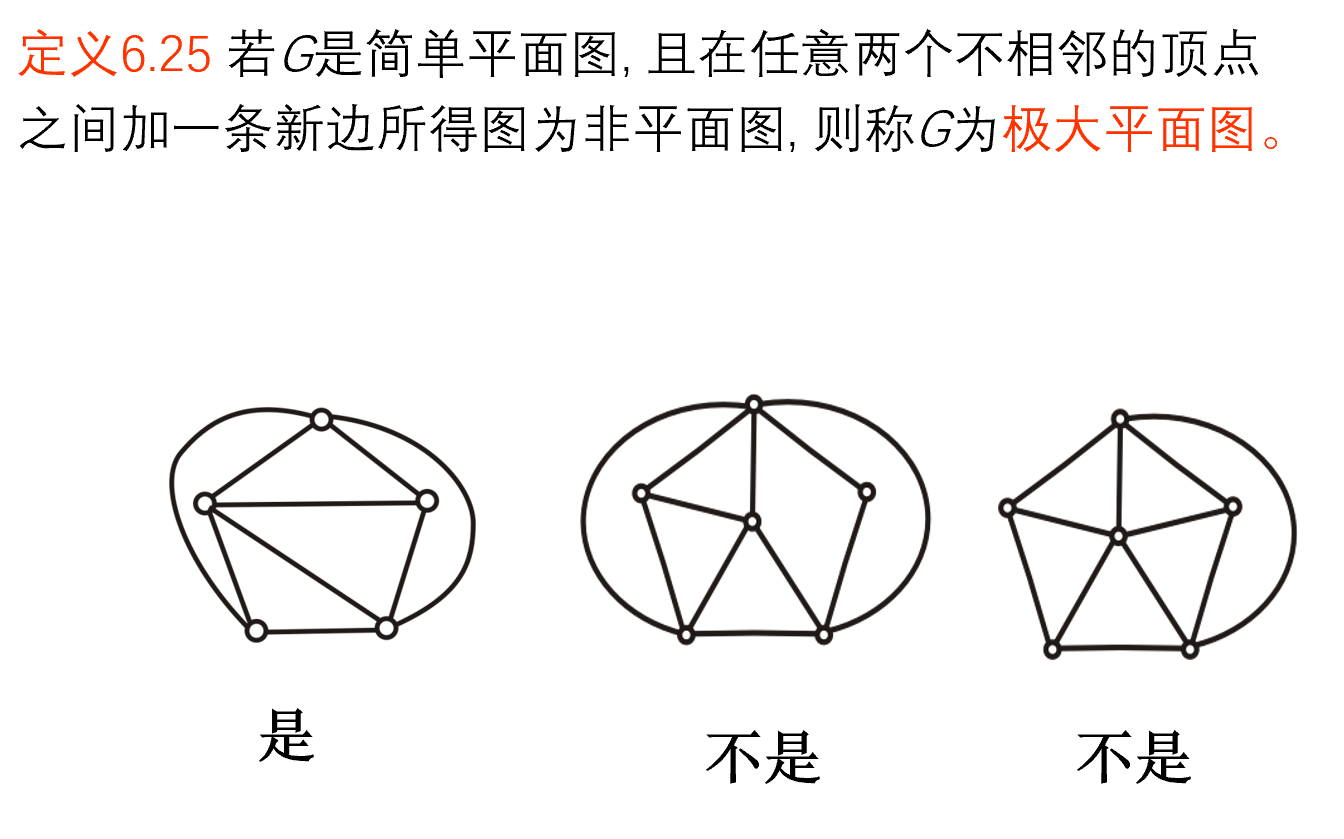
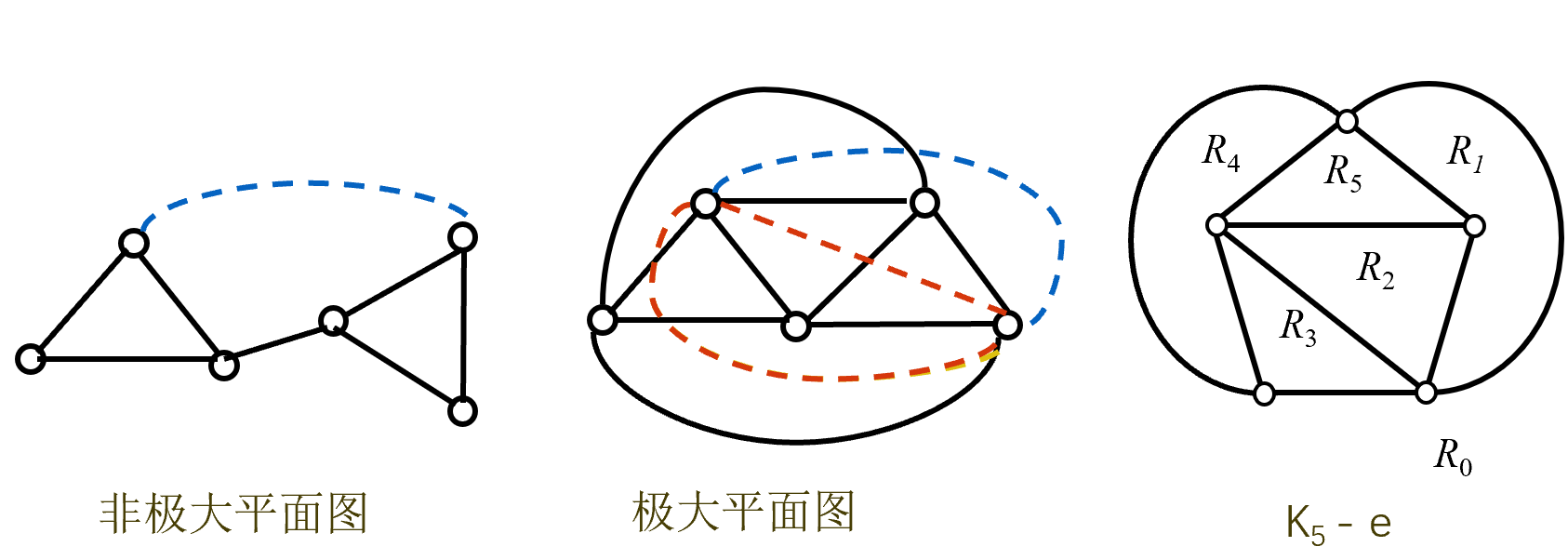
image-20210423154840529 image-20210423155038270 image-20210423155150091
性质
image-20210423160357285
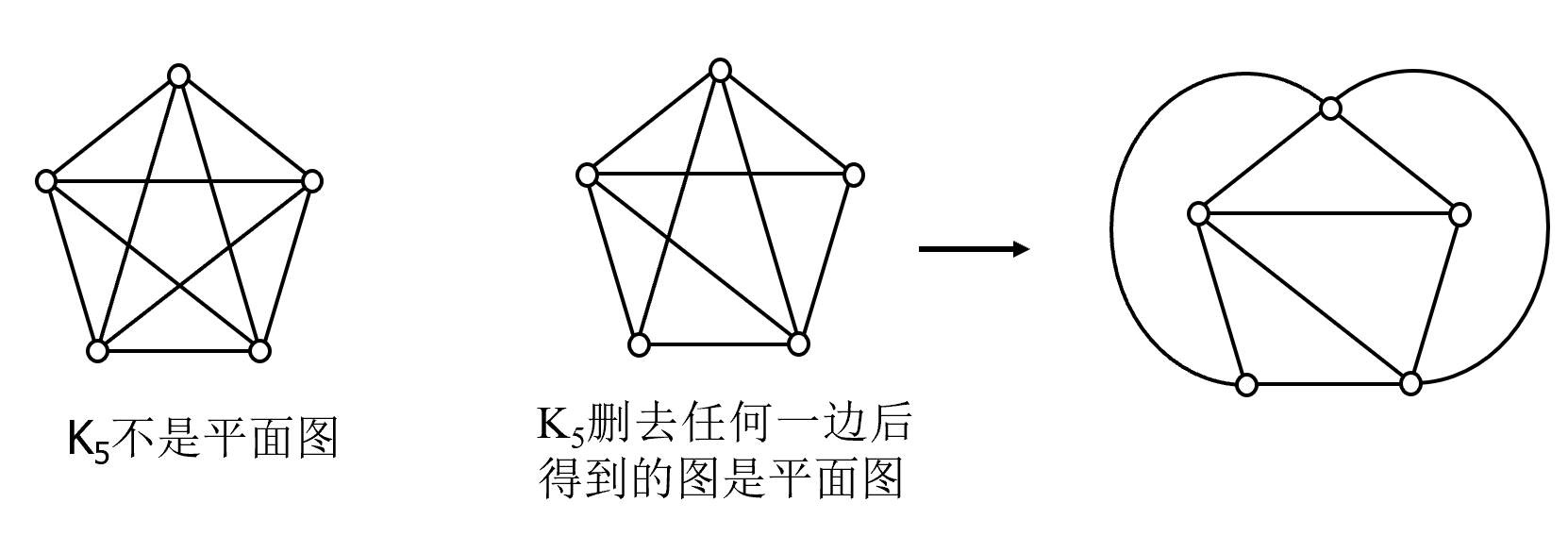
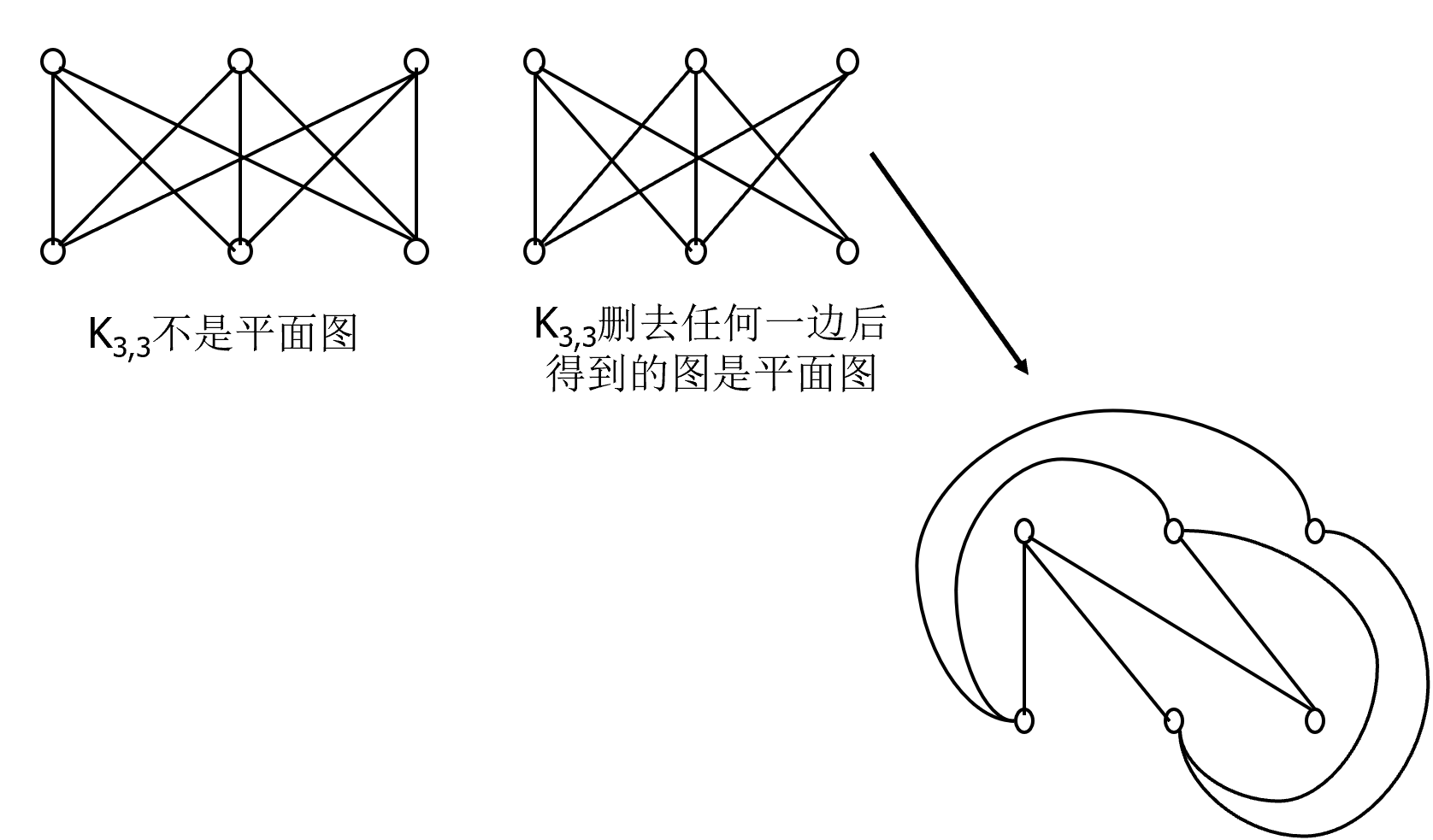
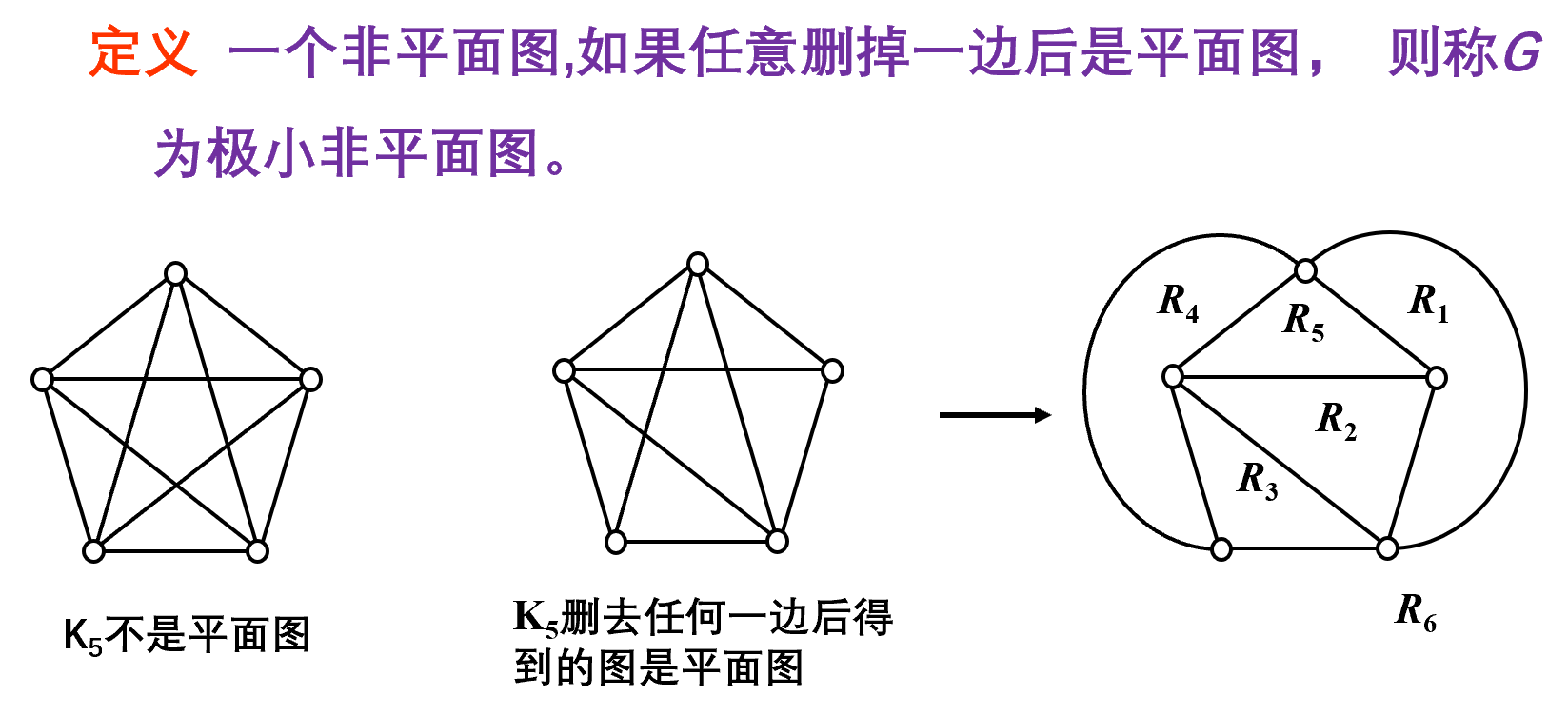
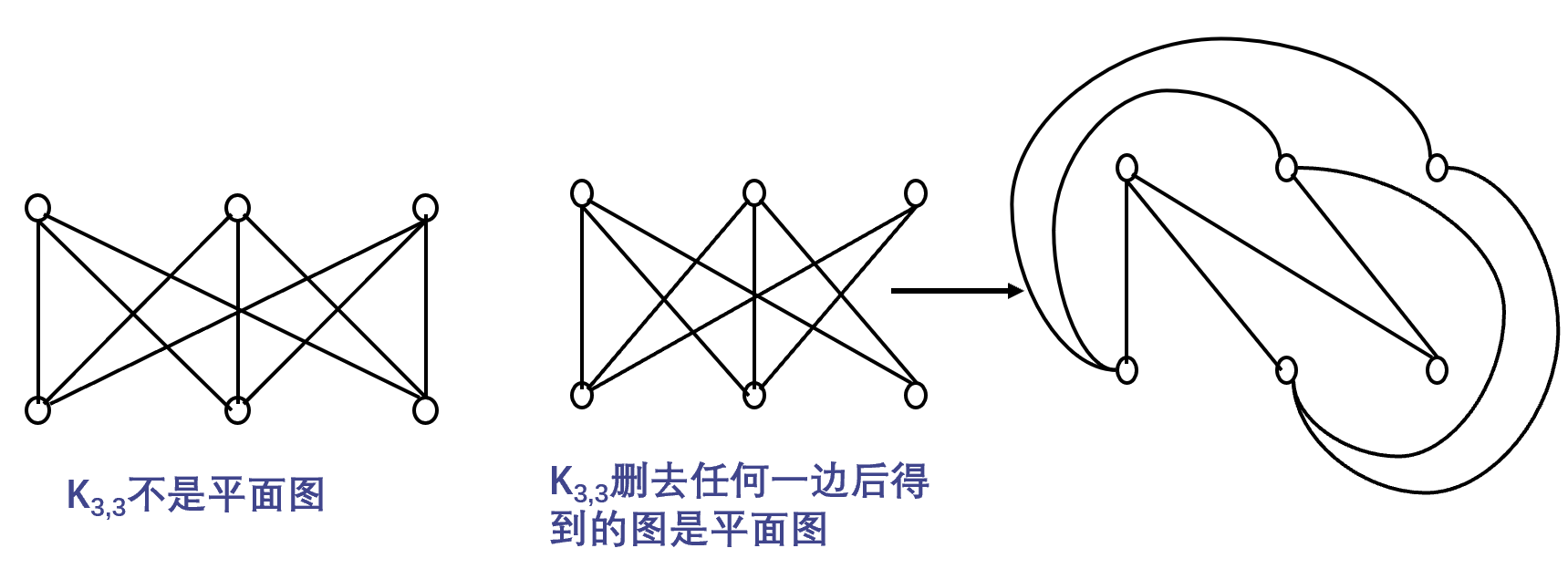
极小非平面图

例子：K~5~ 和 K~3，3~

image-20210423160431134 image-20210423160644997
欧拉公式（重要）
image-20210423160728400
推论
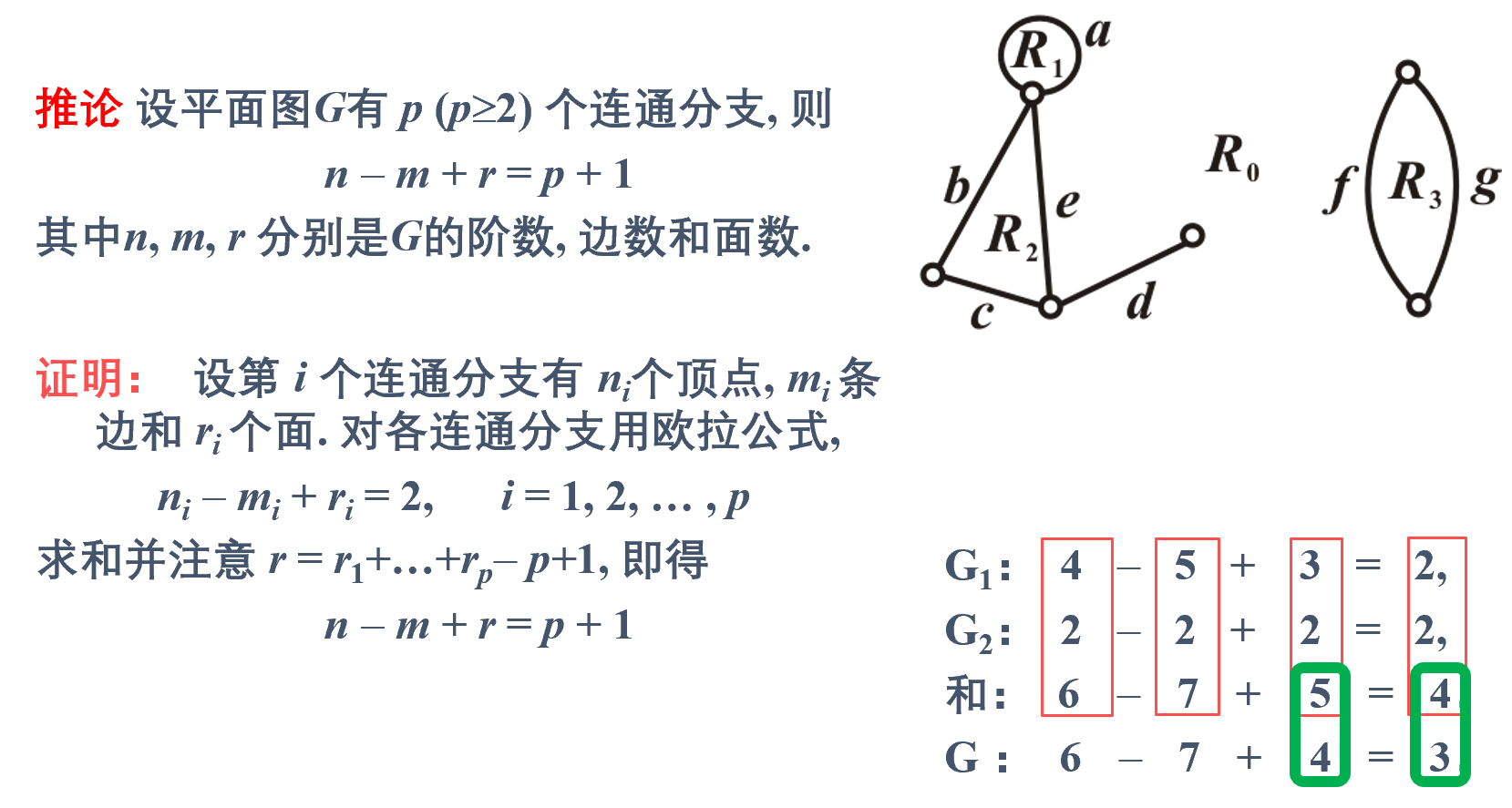
image-20210423161521032
推广
image-20210423161610613
例
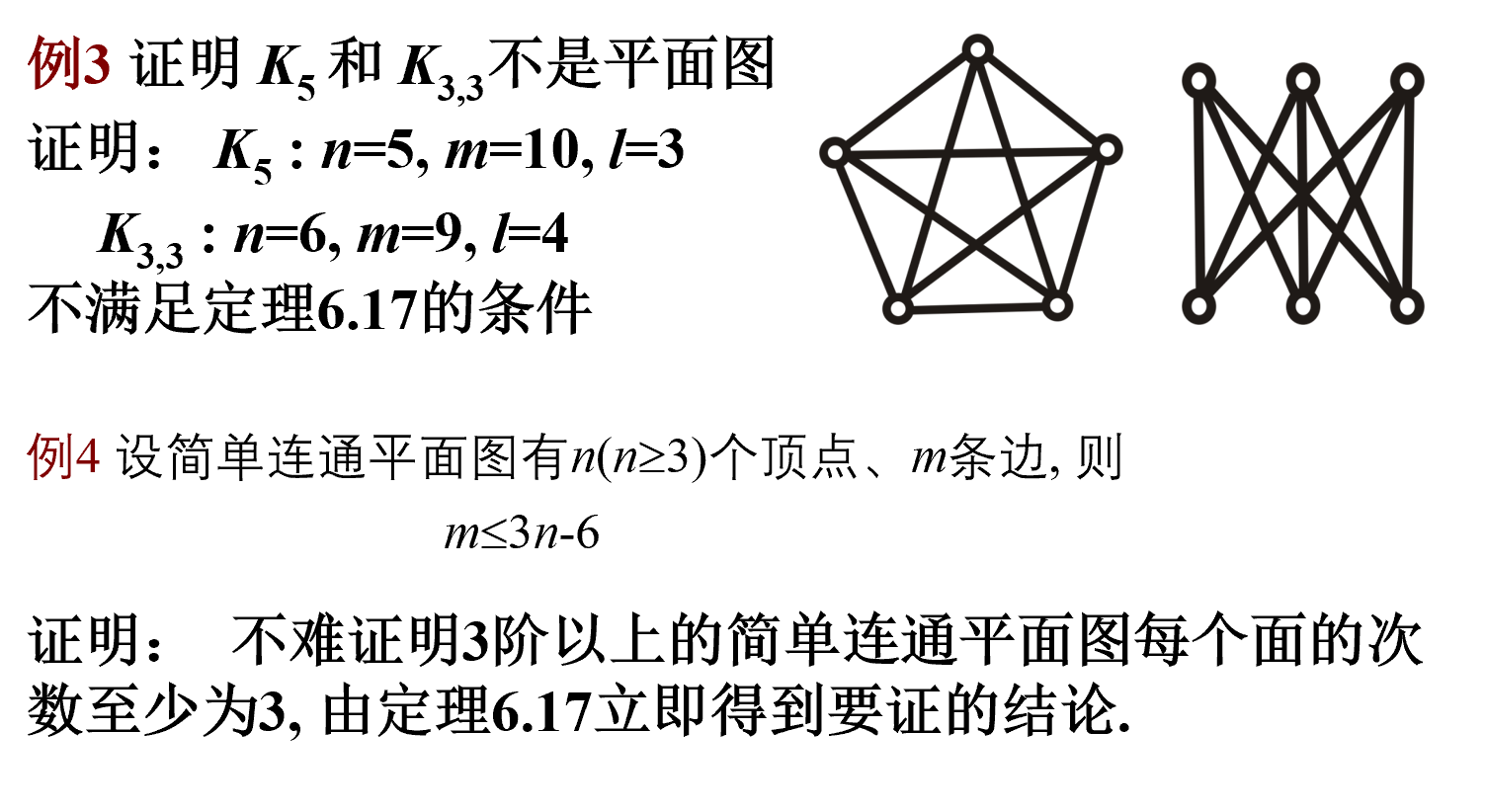
image-20210423161640110
库拉图斯基定理
同胚与收缩
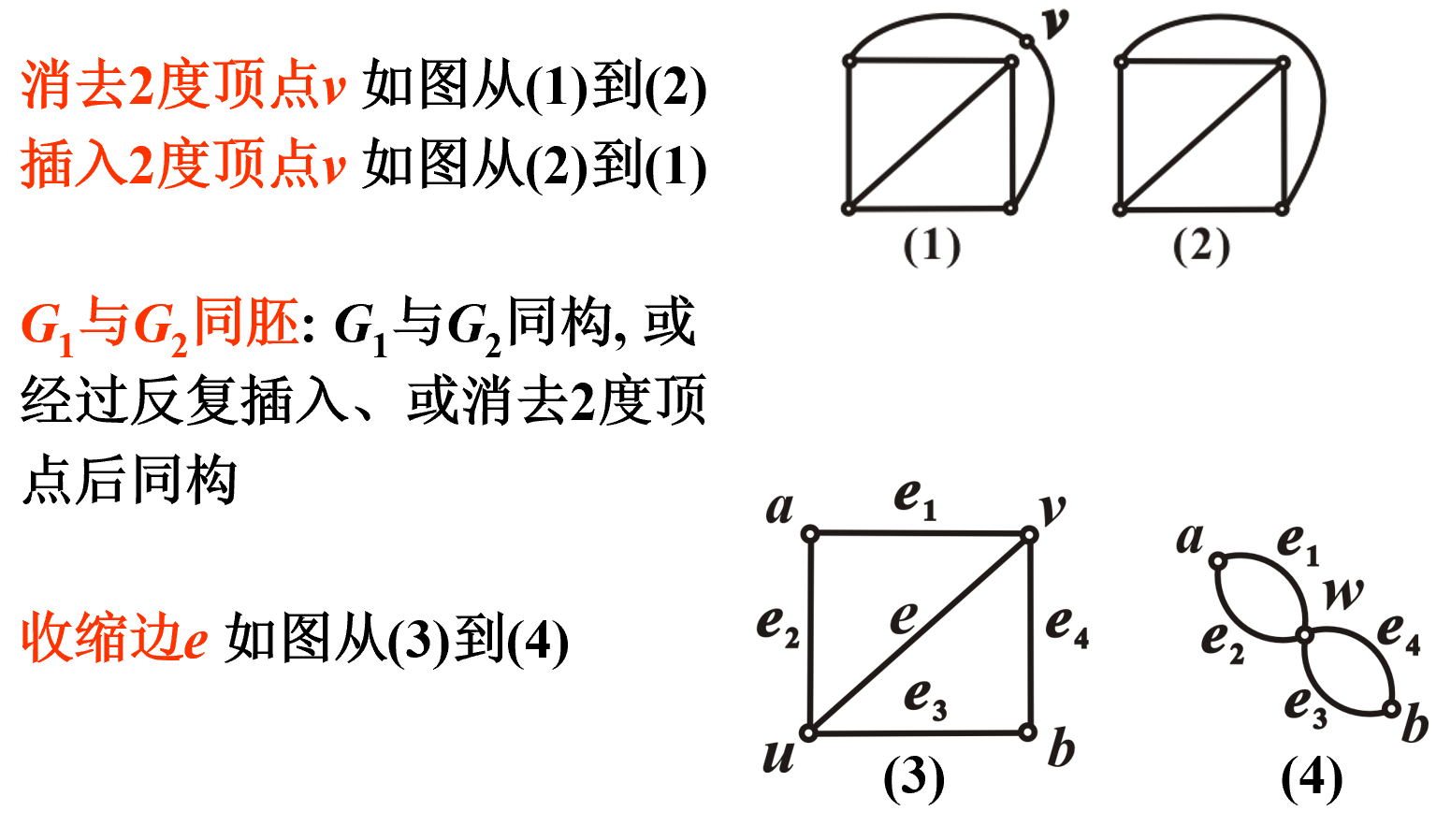
image-20210423162252743
定理
image-20210423162400341
例
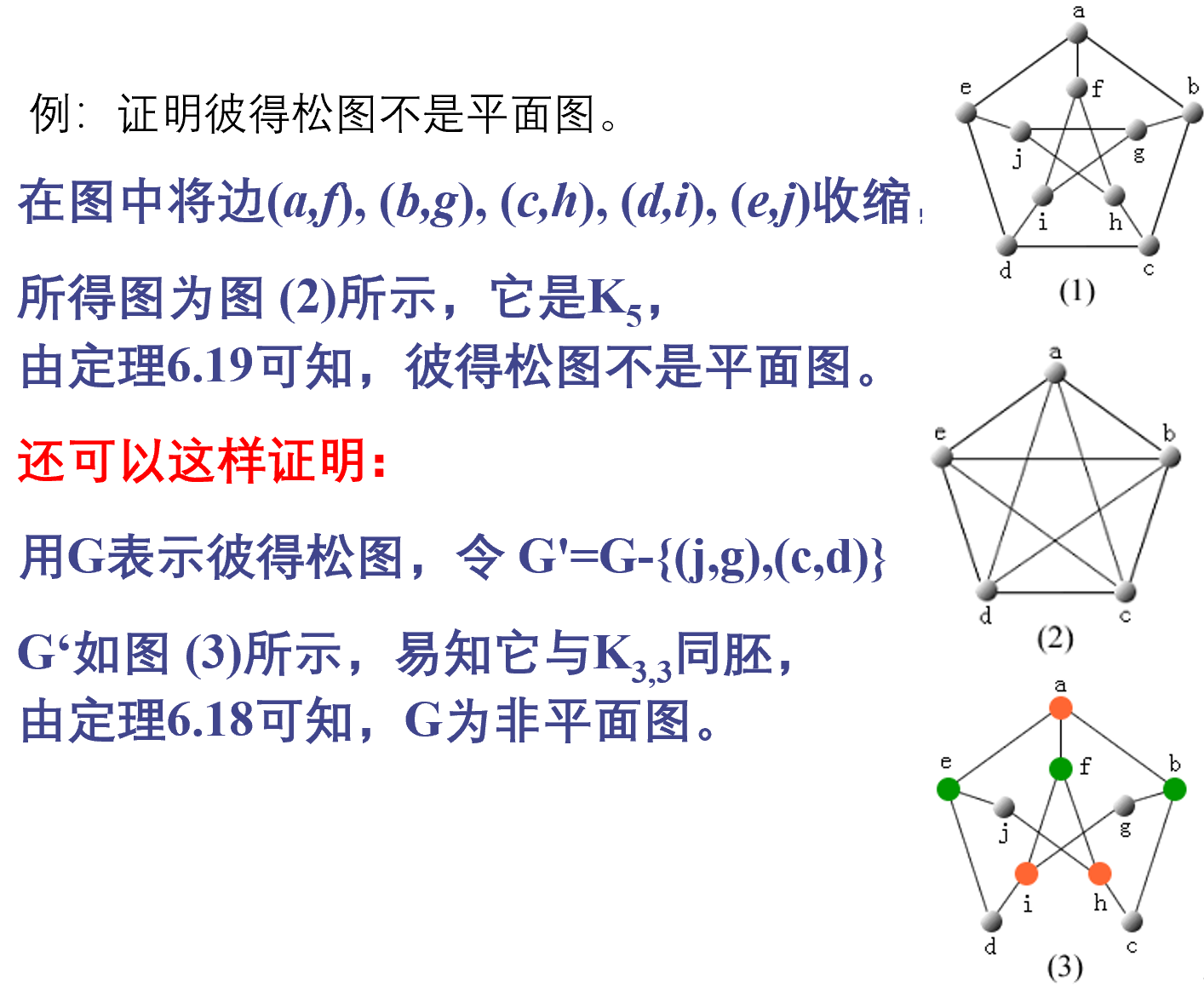
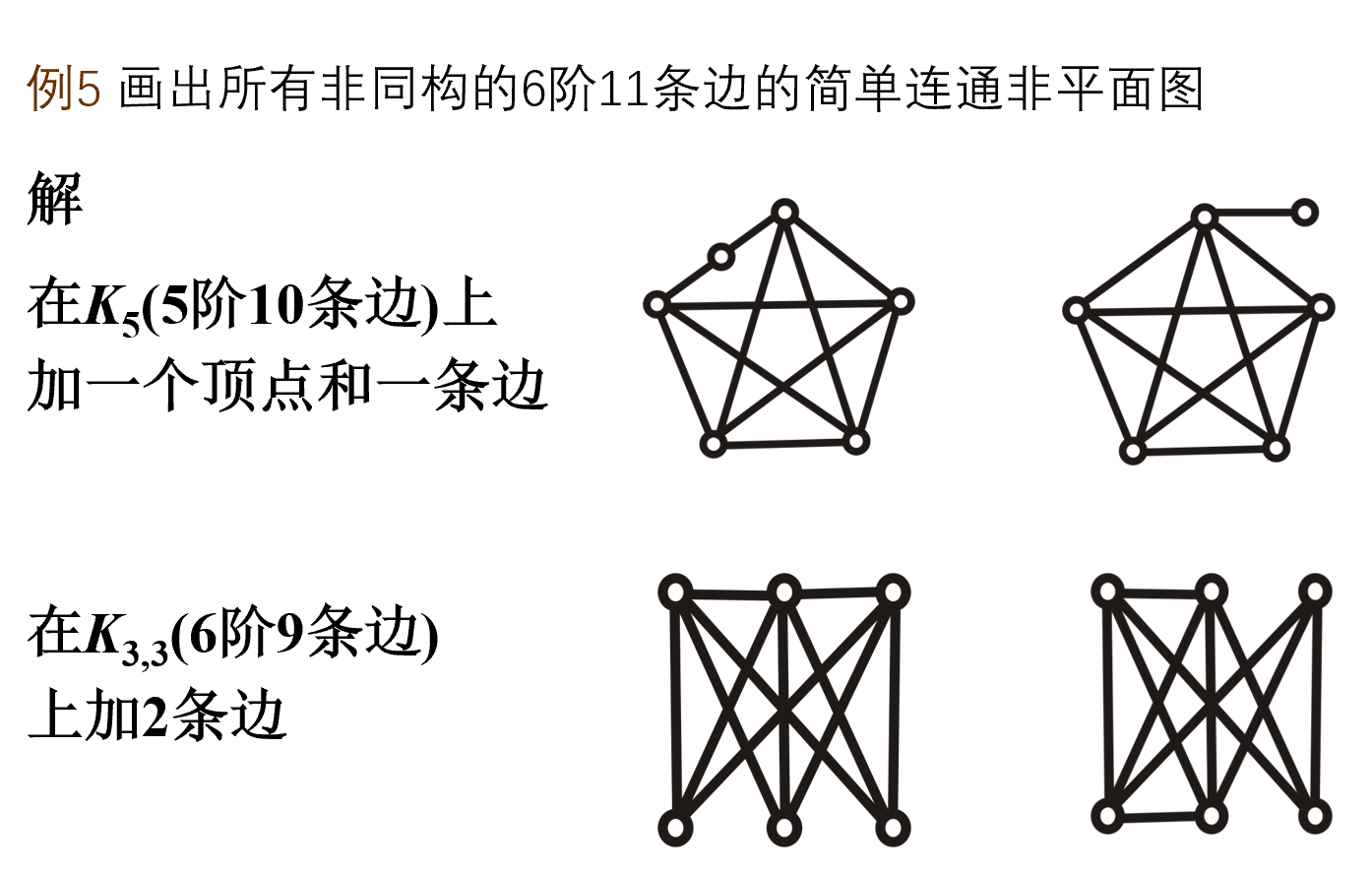
image-20210423163541642 image-20210423163223552
平面图的对偶图
定义
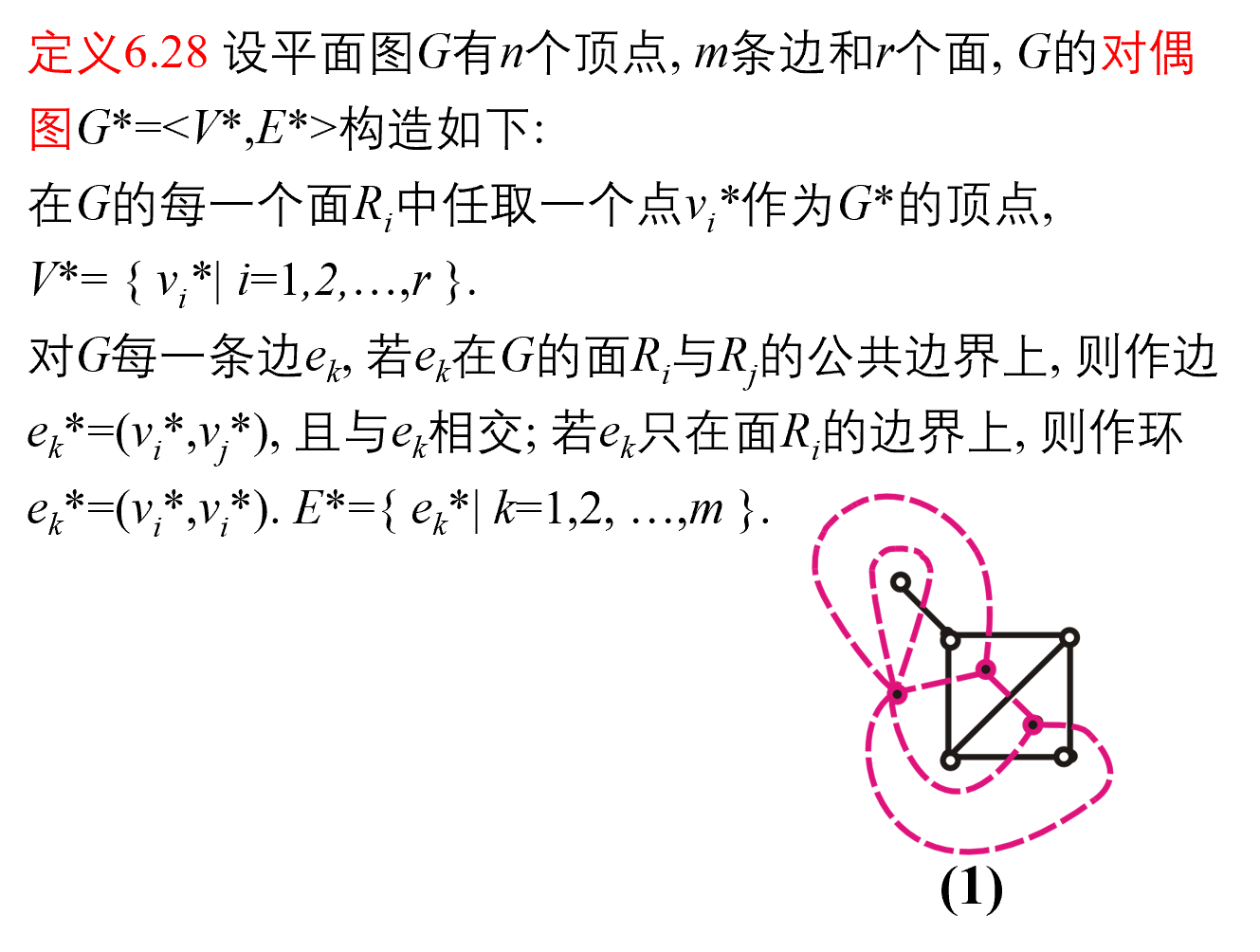
image-20210423163309187
性质
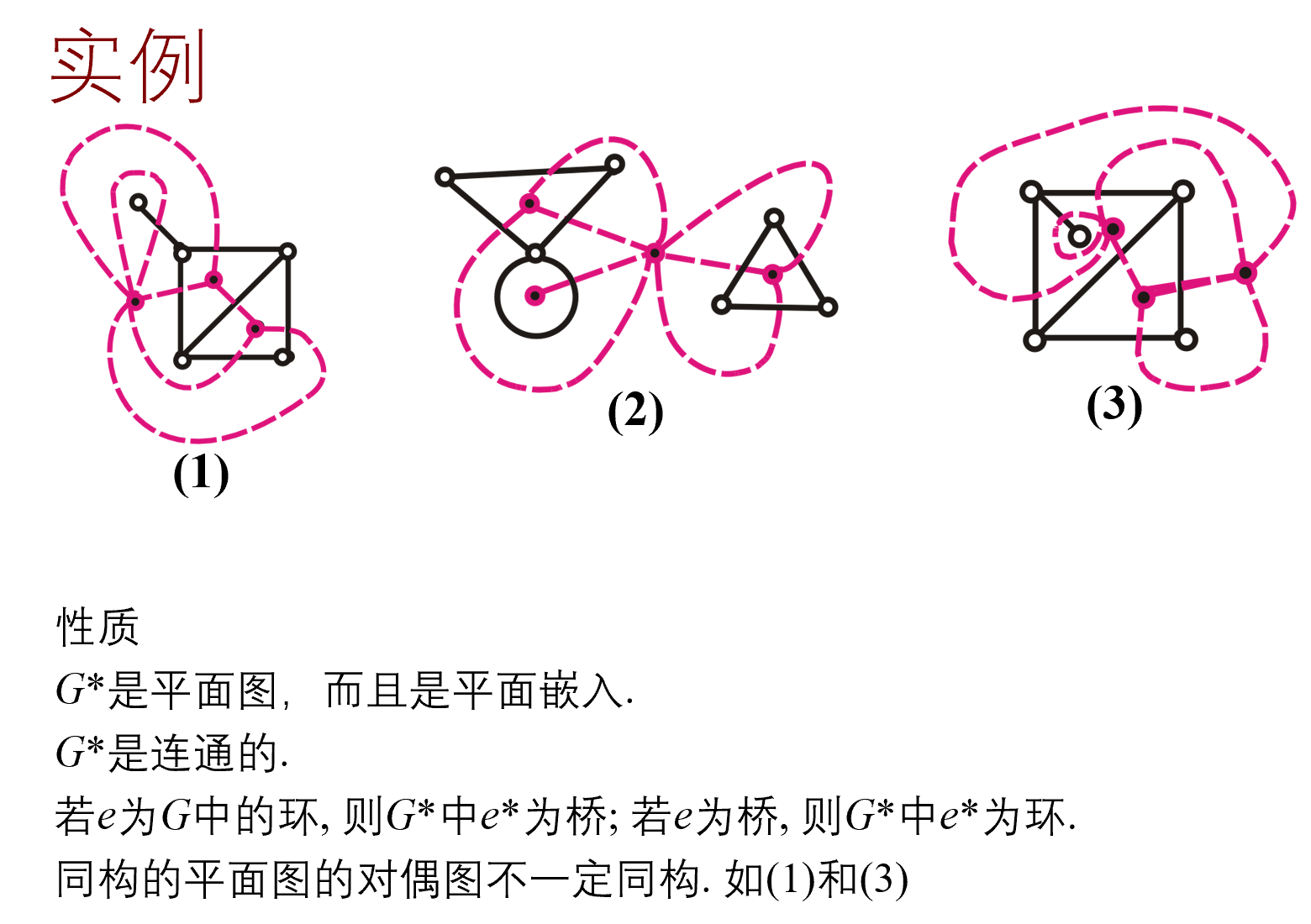
image-20210423163344150
定理
image-20210423163922143

树

只学习无向树

定义

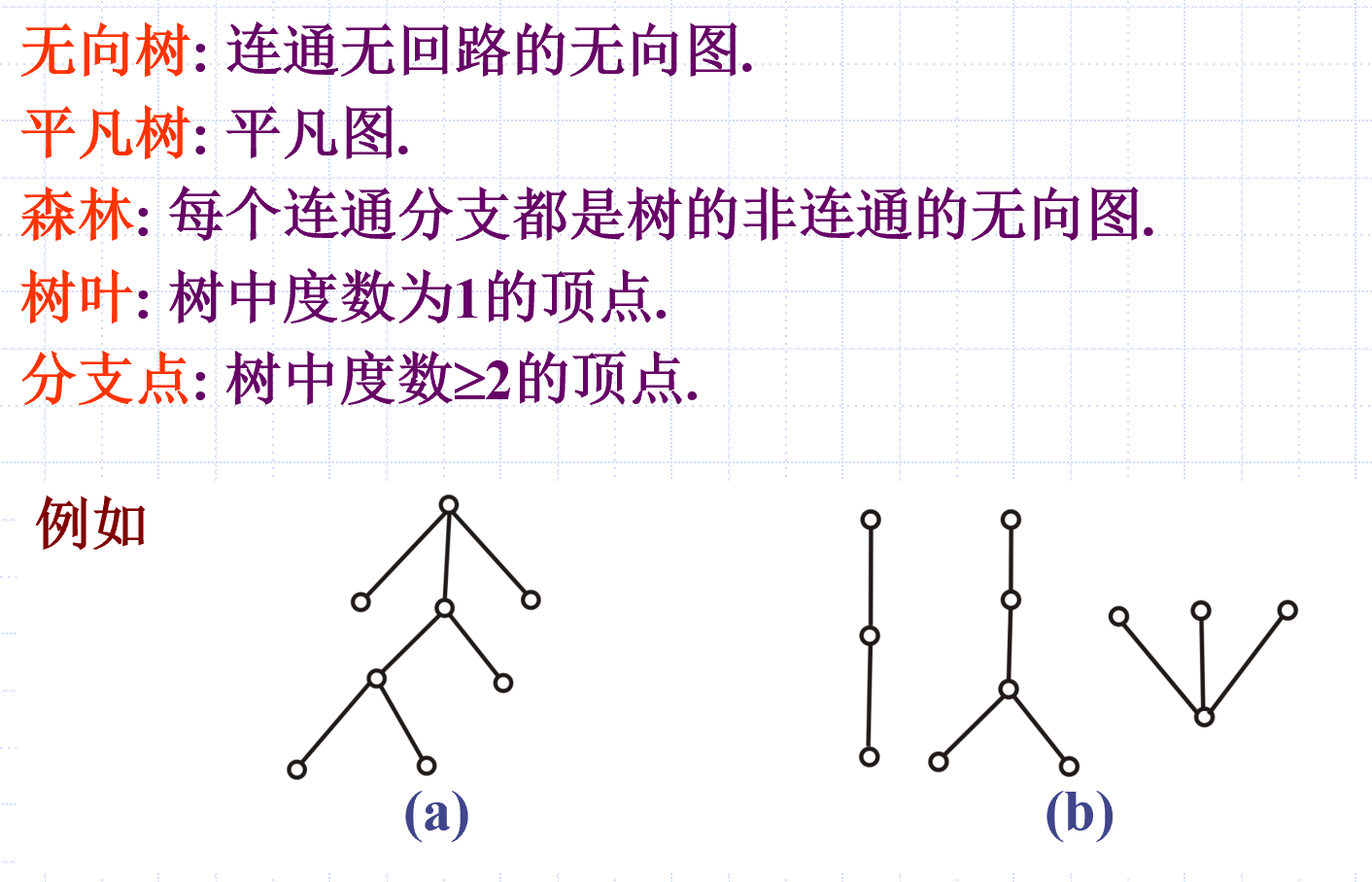
image-20210430141401205

性质

image-20210430141459112 image-20210430151946032

证明

image-20210430142336283 image-20210430142936073 image-20210430142947314 image-20210430142959903 image-20210430143013763 image-20210430143038169 image-20210430143052863

其他性质

image-20210430144449829

树与各种特殊图的关系

  • 树是二部图

  • 树一定不是欧拉图（没有回路）

  • 树一定不是哈密顿图（没有回路）

  • 树一定是平面图

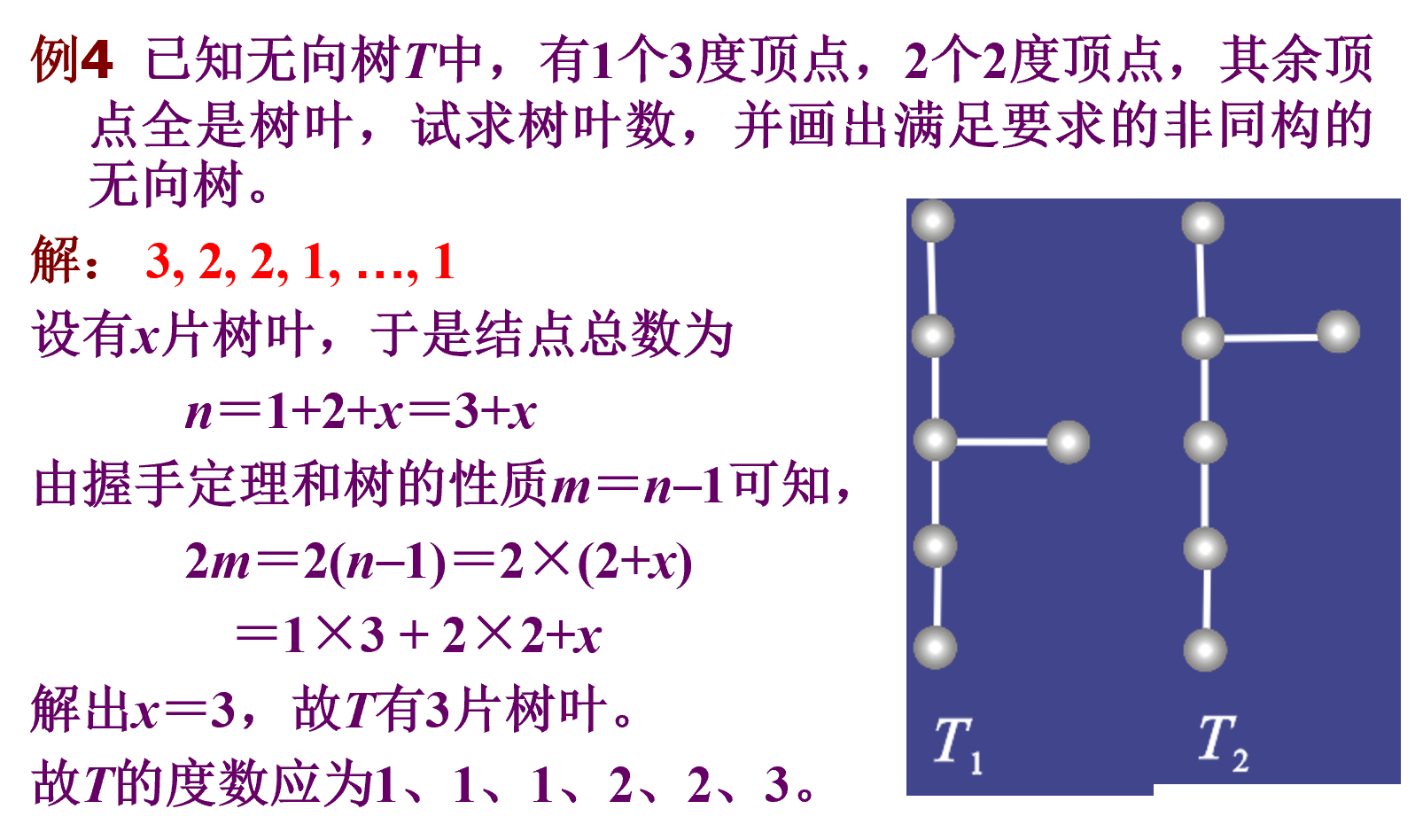
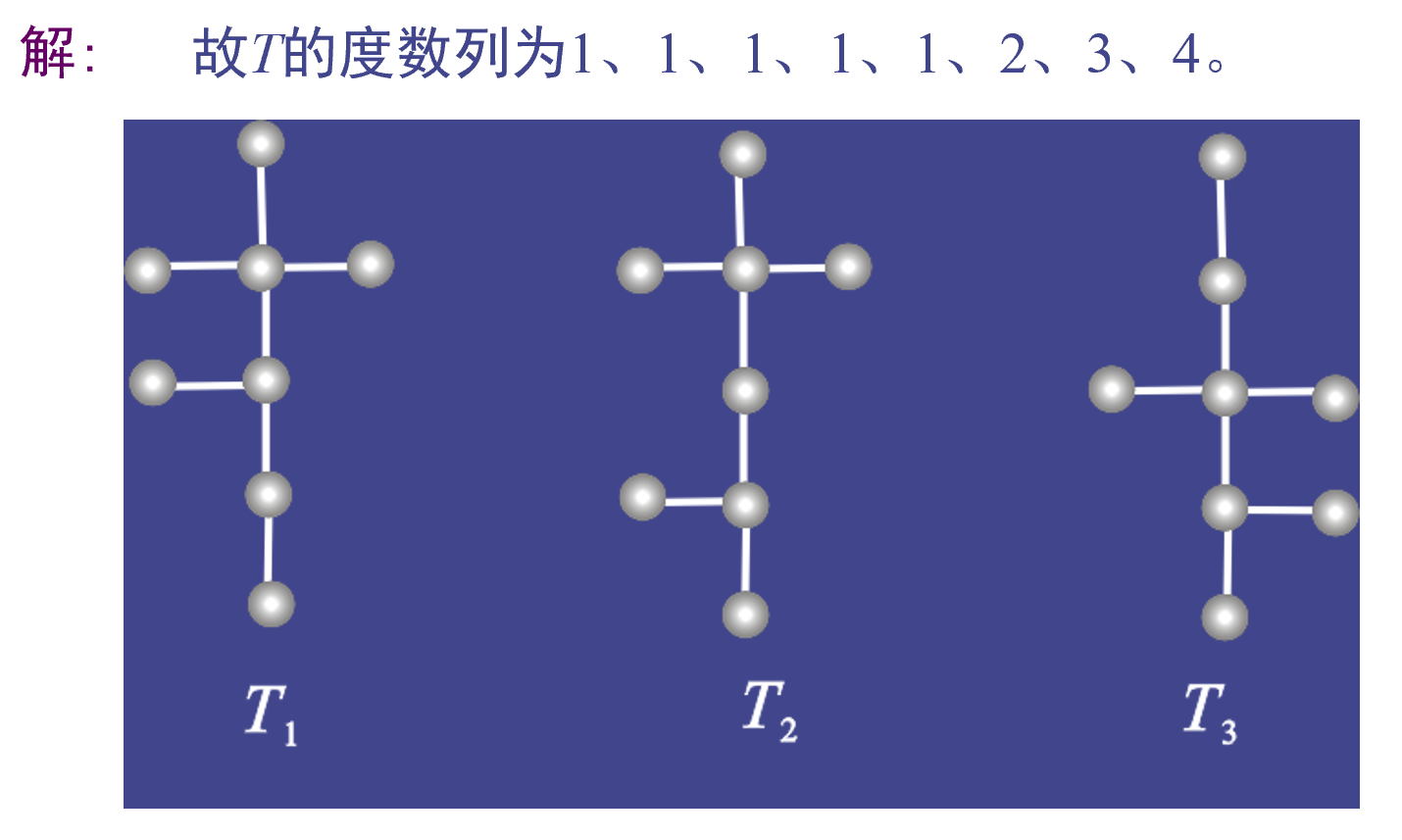
实例

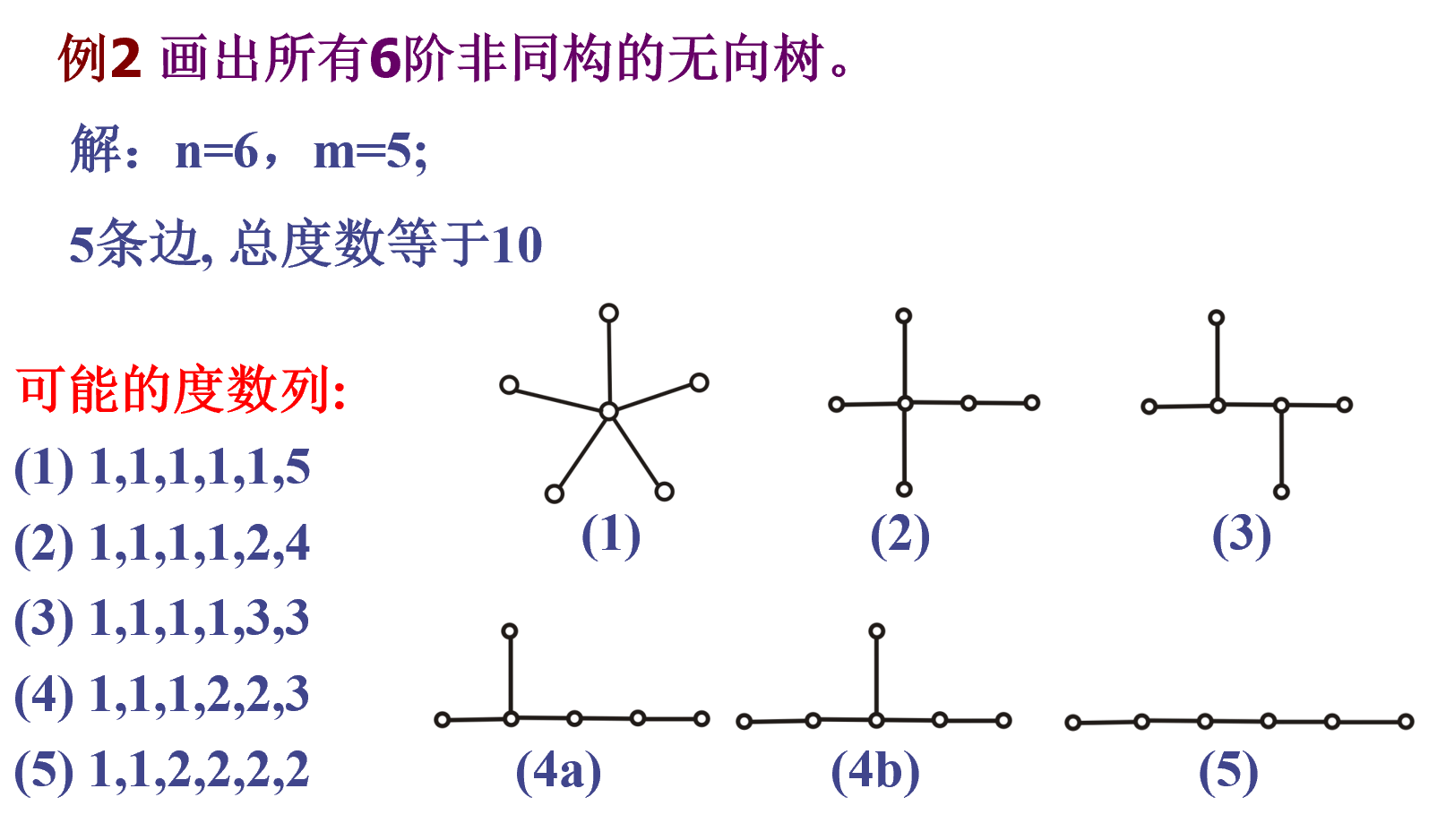
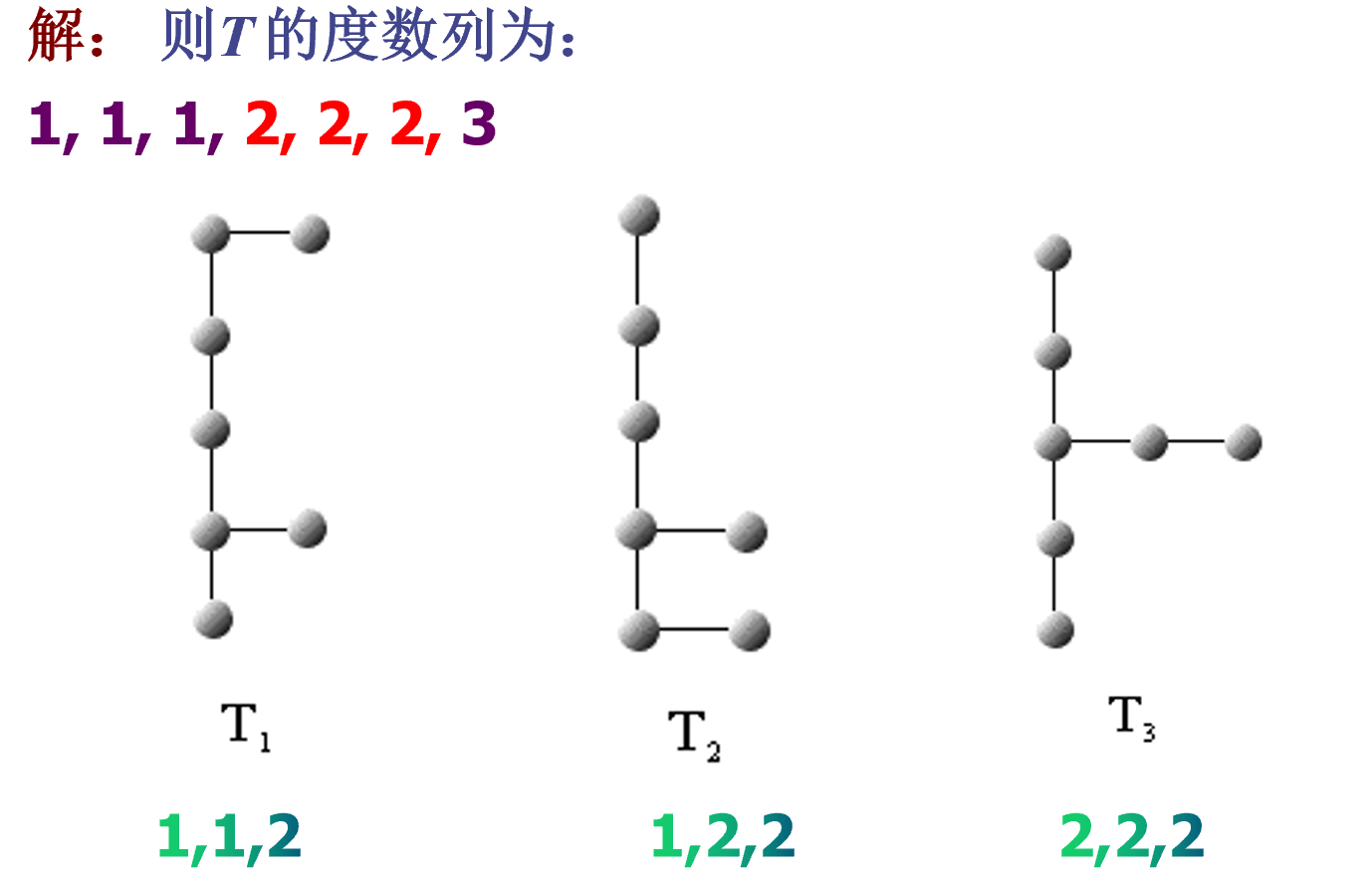
image-20210430152941974 image-20210430153640471 image-20210430153740764 image-20210430153755417 image-20210430153808247 image-20210430154121973 image-20210430154133272

生成树

定义

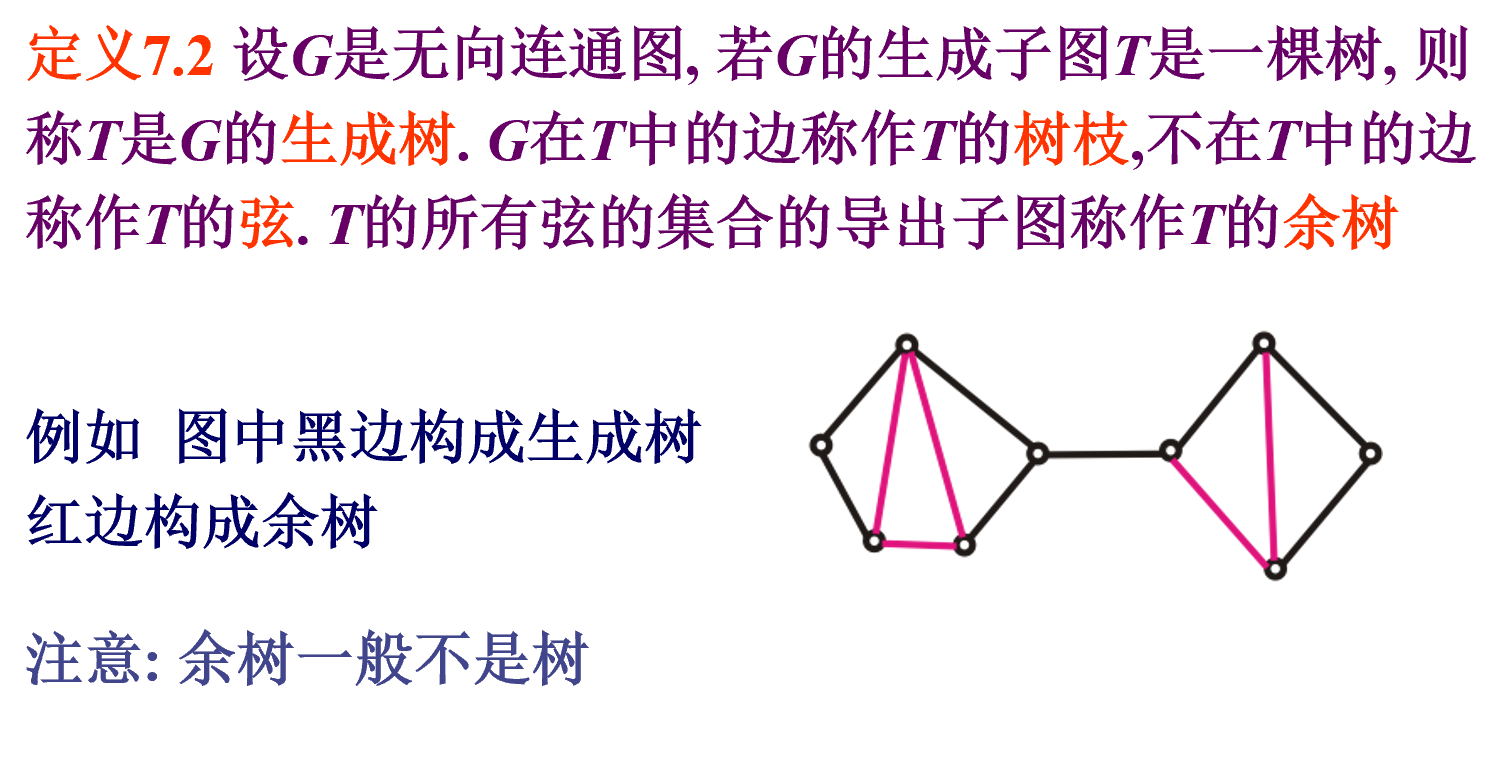
image-20210430154230874

存在

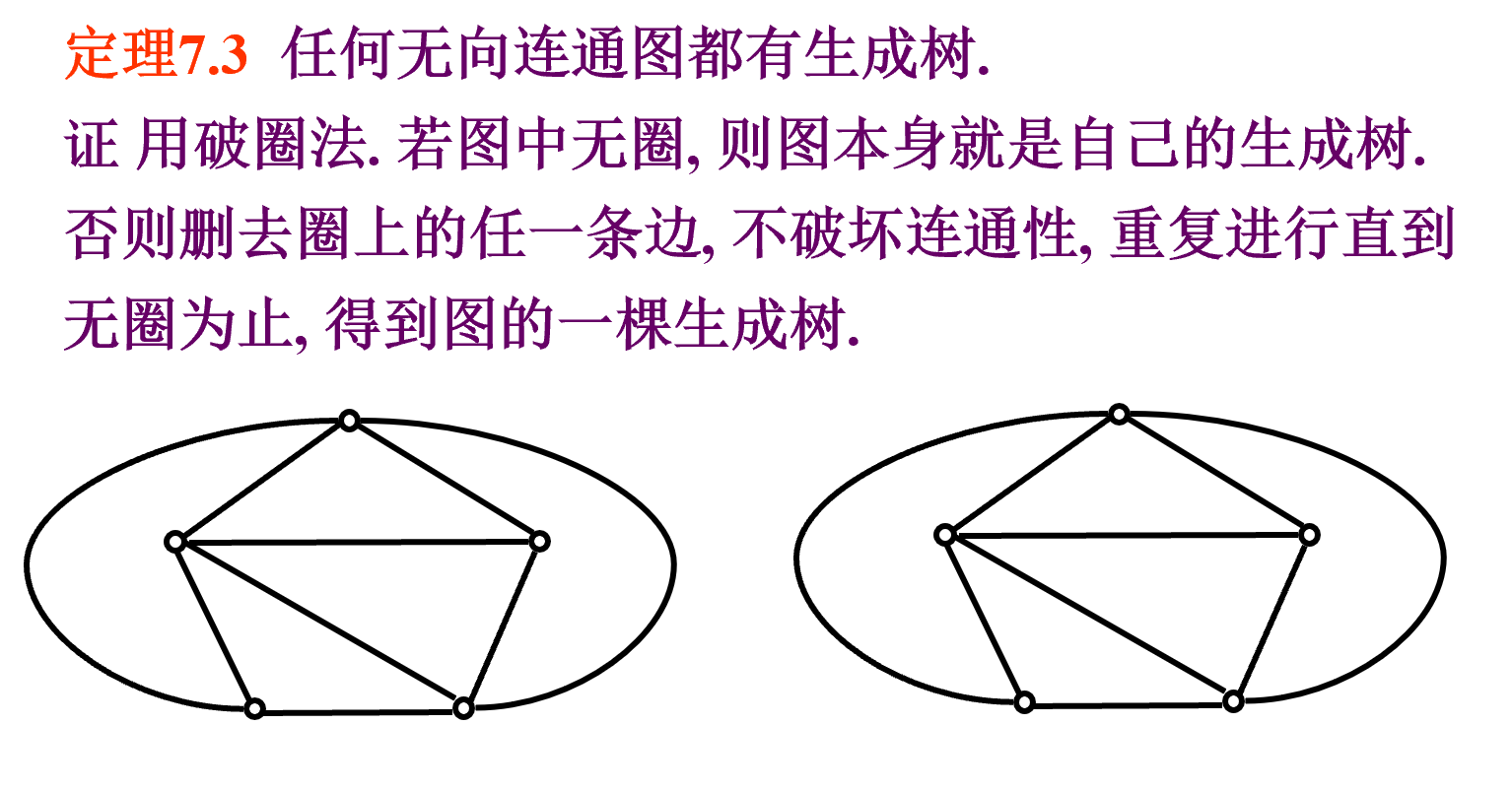
image-20210430154324196 image-20210430154417978

最小生成树

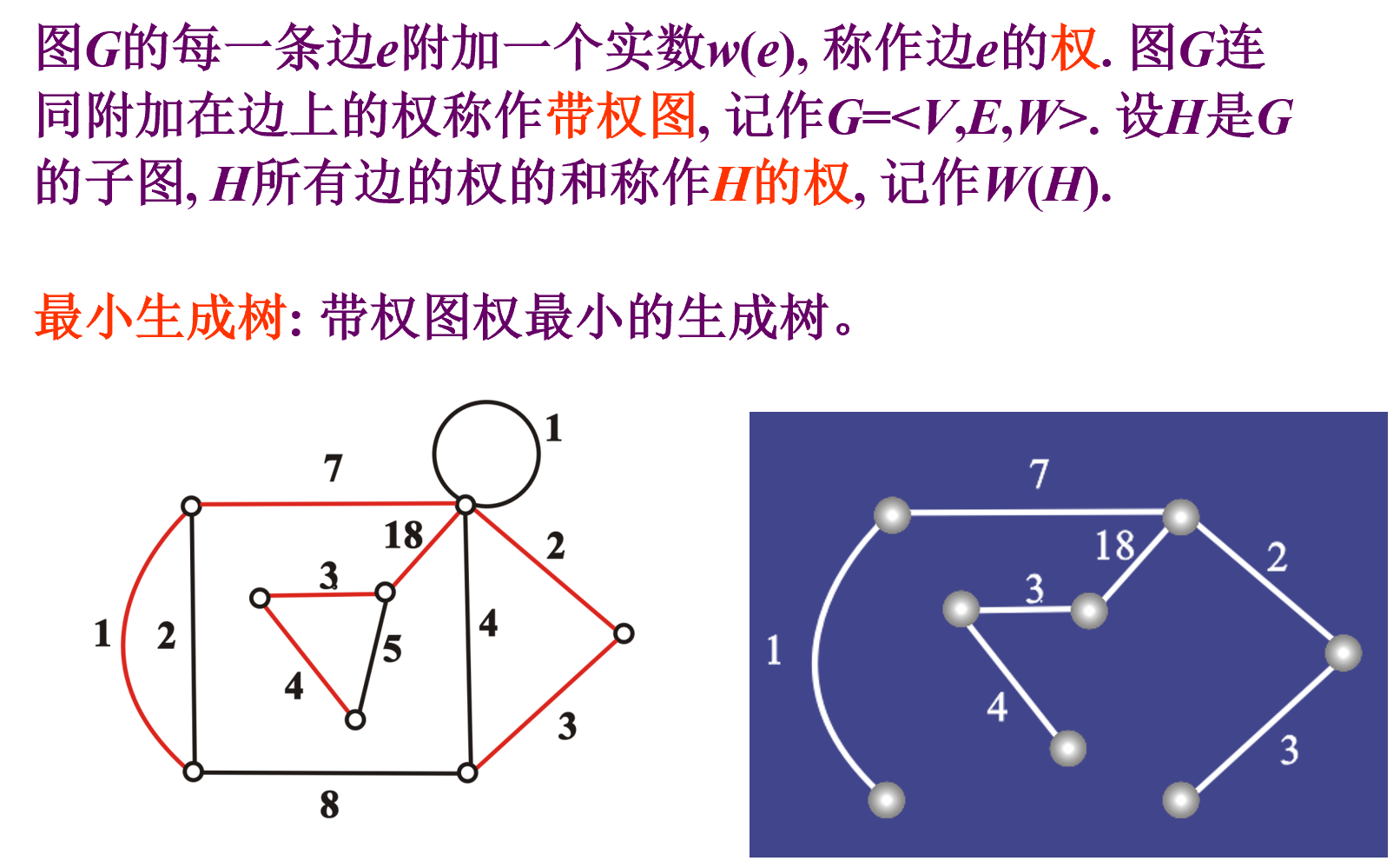
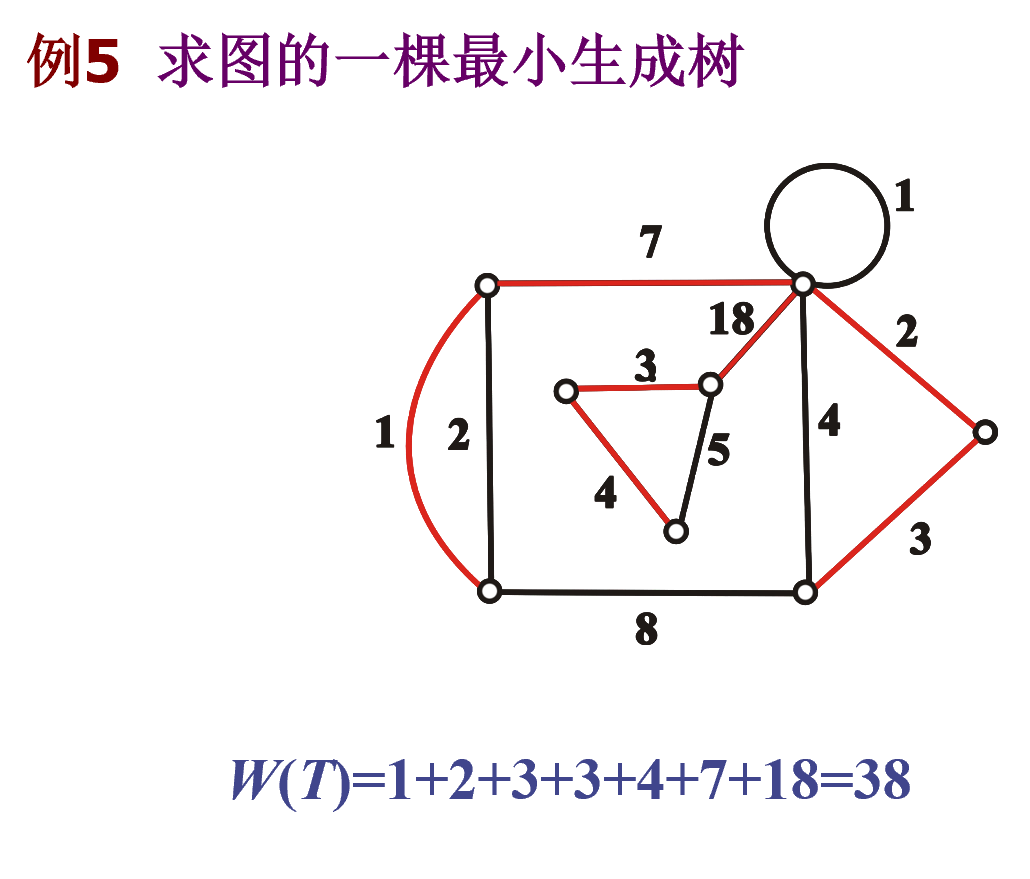
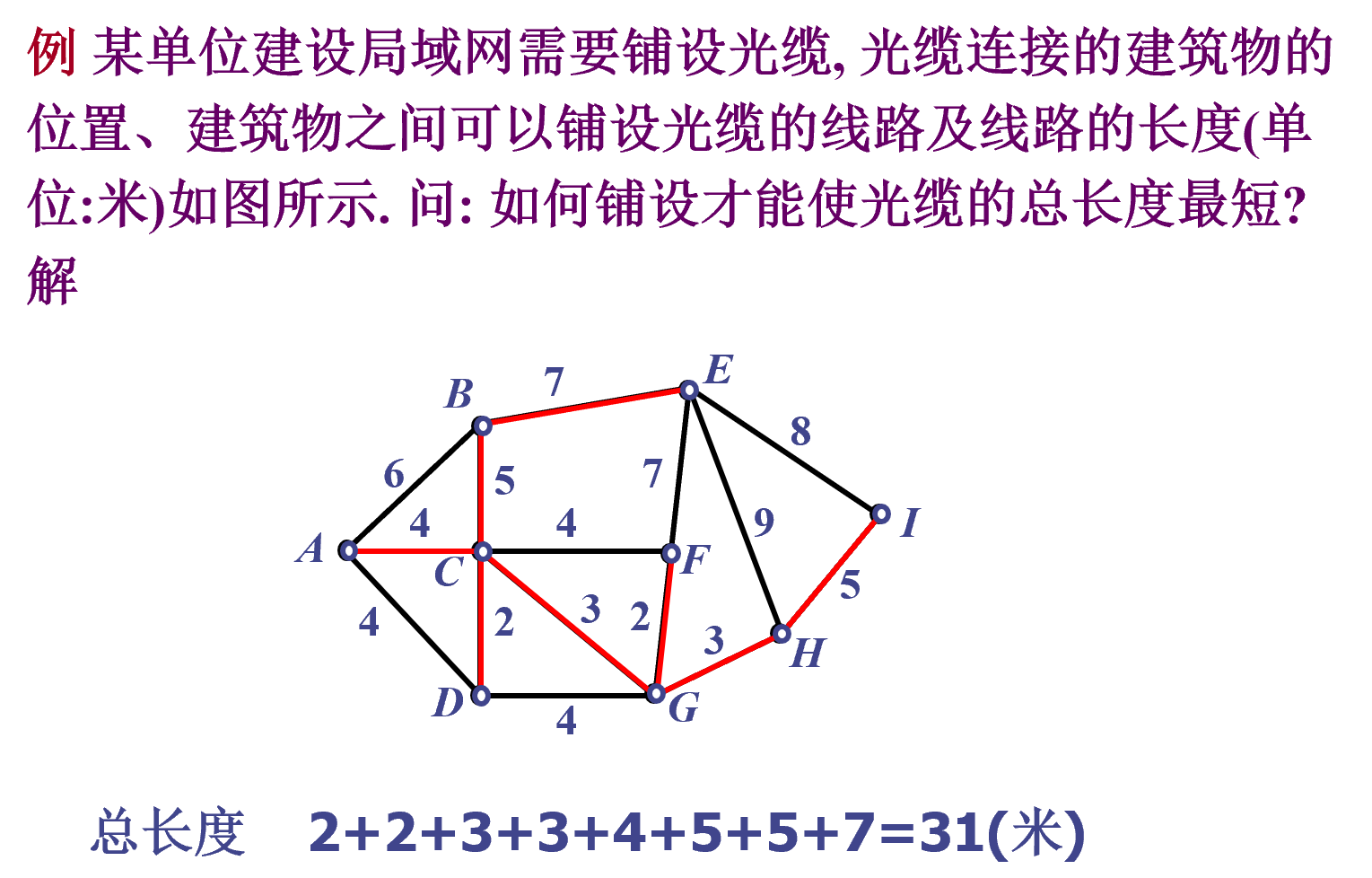
image-20210430154450862 image-20210430160945449 image-20210430161002107 image-20210430161013033

代数系统

二元运算及其性质

二元运算与一元运算的定义

运算 -> 函数 -> 关系 $\langle\langle x,y\rangle,z \rangle$

二元运算
image-20210507141537653
一元运算
image-20210507142123419
算符
image-20210507142230569 image-20210507142245156
运算表
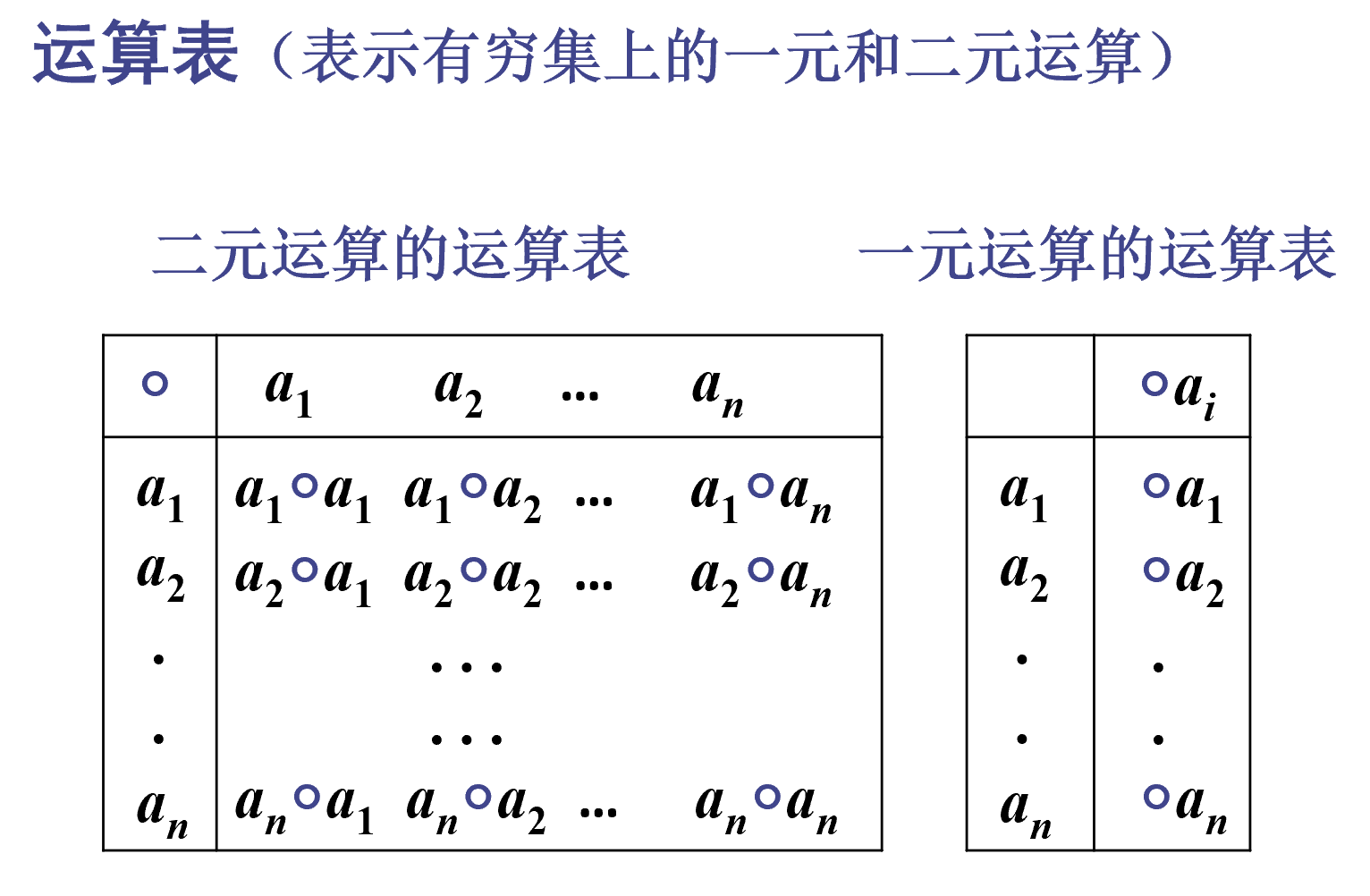
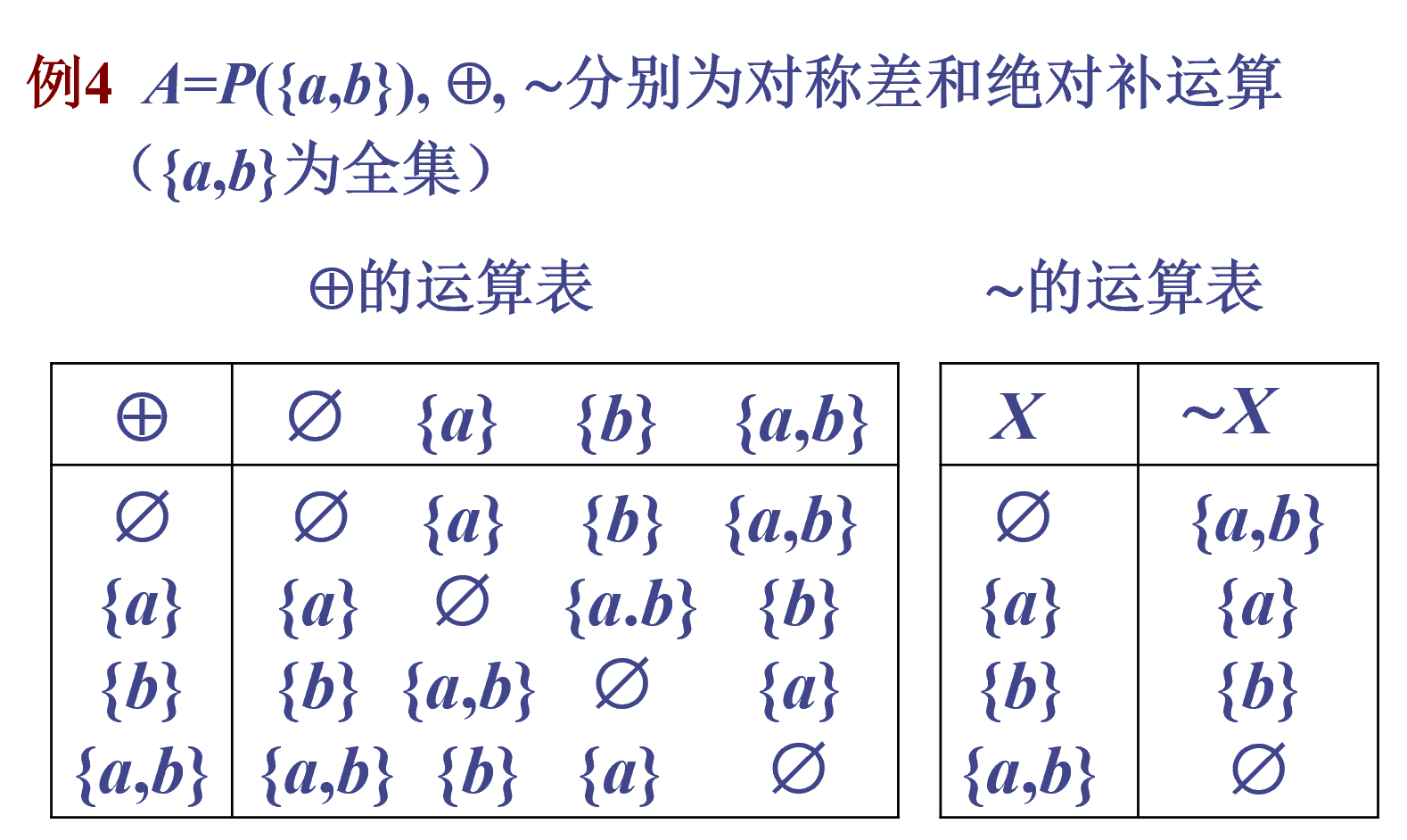
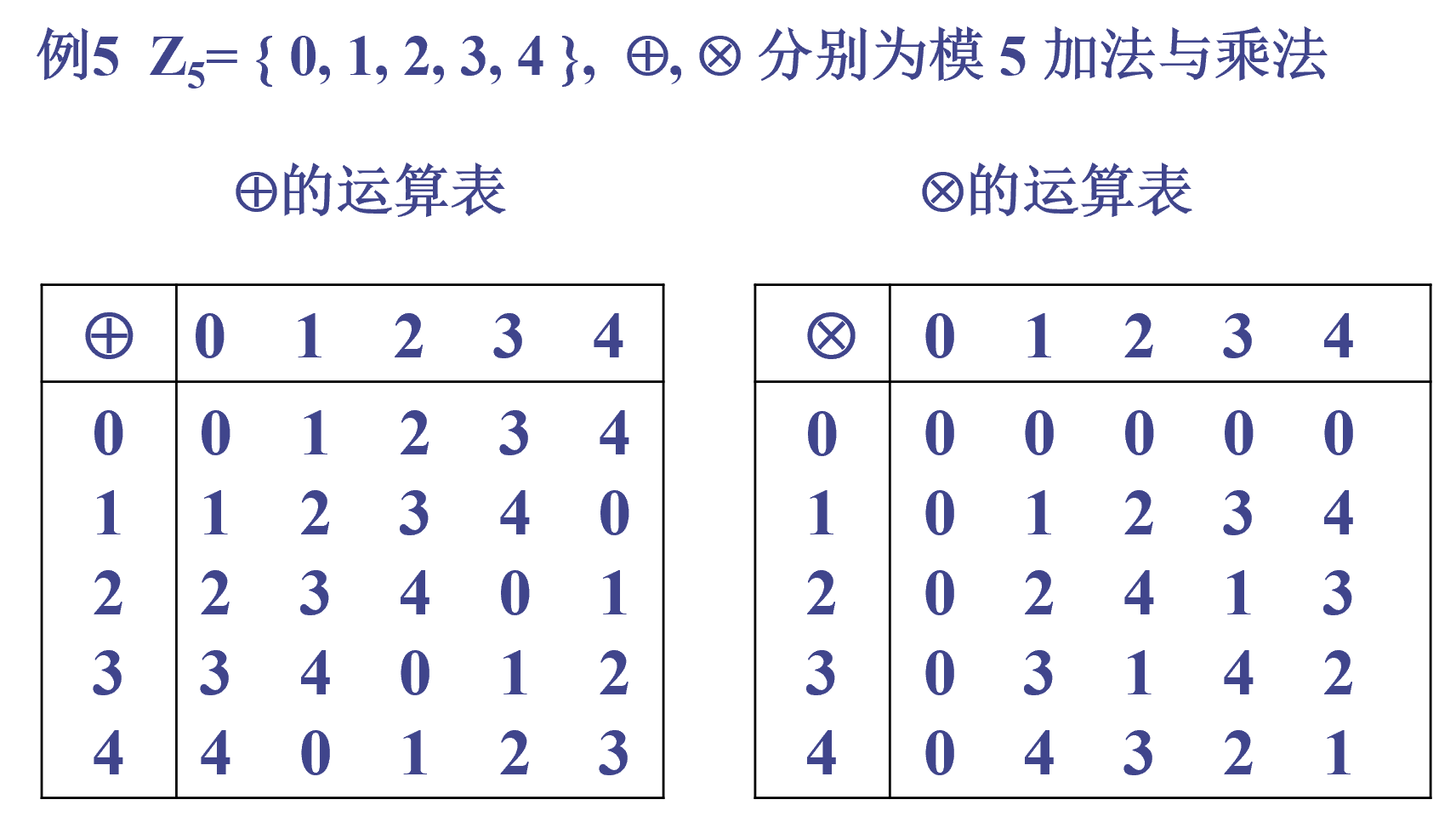
image-20210507142919318 image-20210507142952706 image-20210507143003905

二元运算的性质

交换、结合、幂等
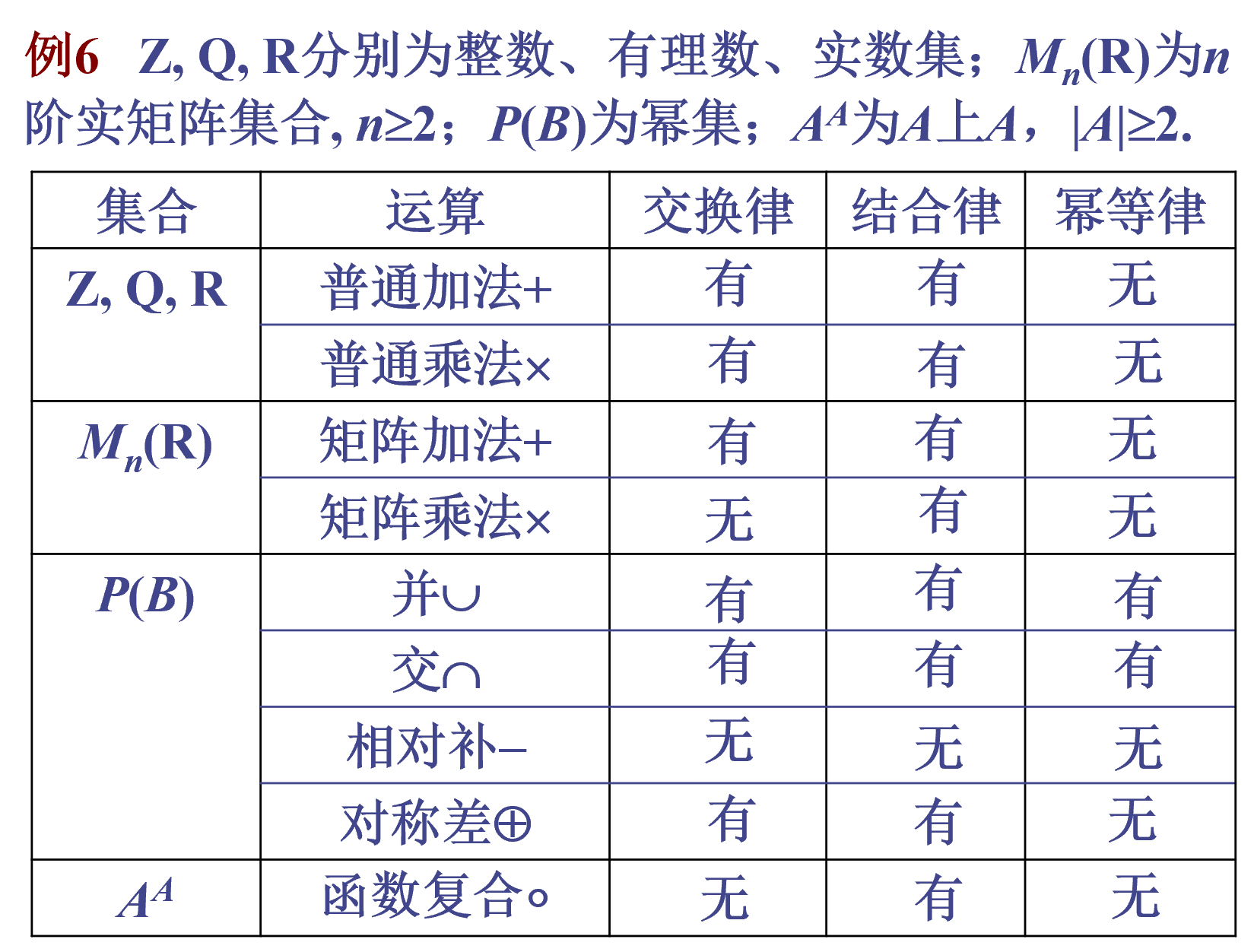
image-20210507143016416 image-20210507143345852
分配、吸收
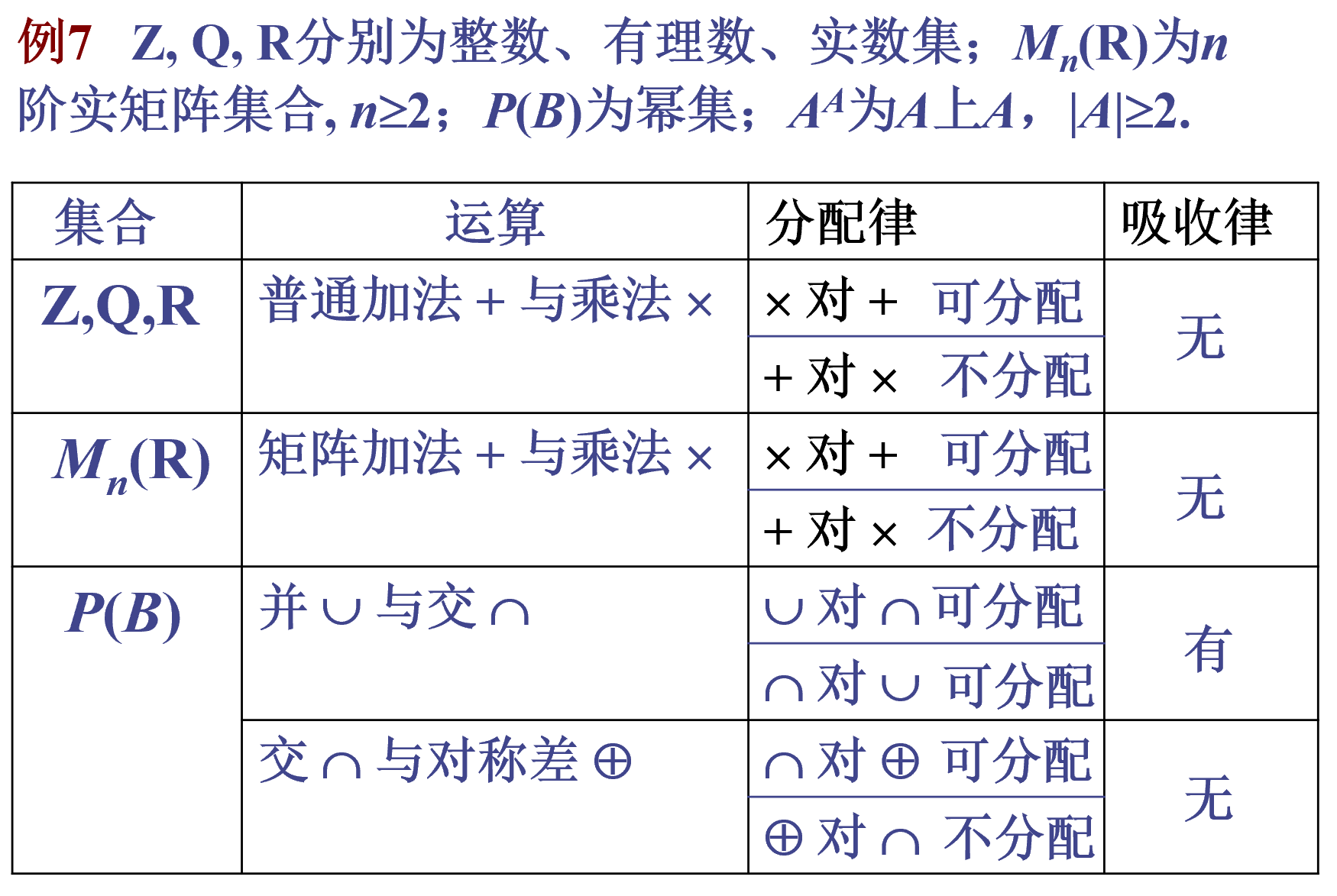
image-20210507144242929 image-20210507144624183

二元运算的特异元素

单位元
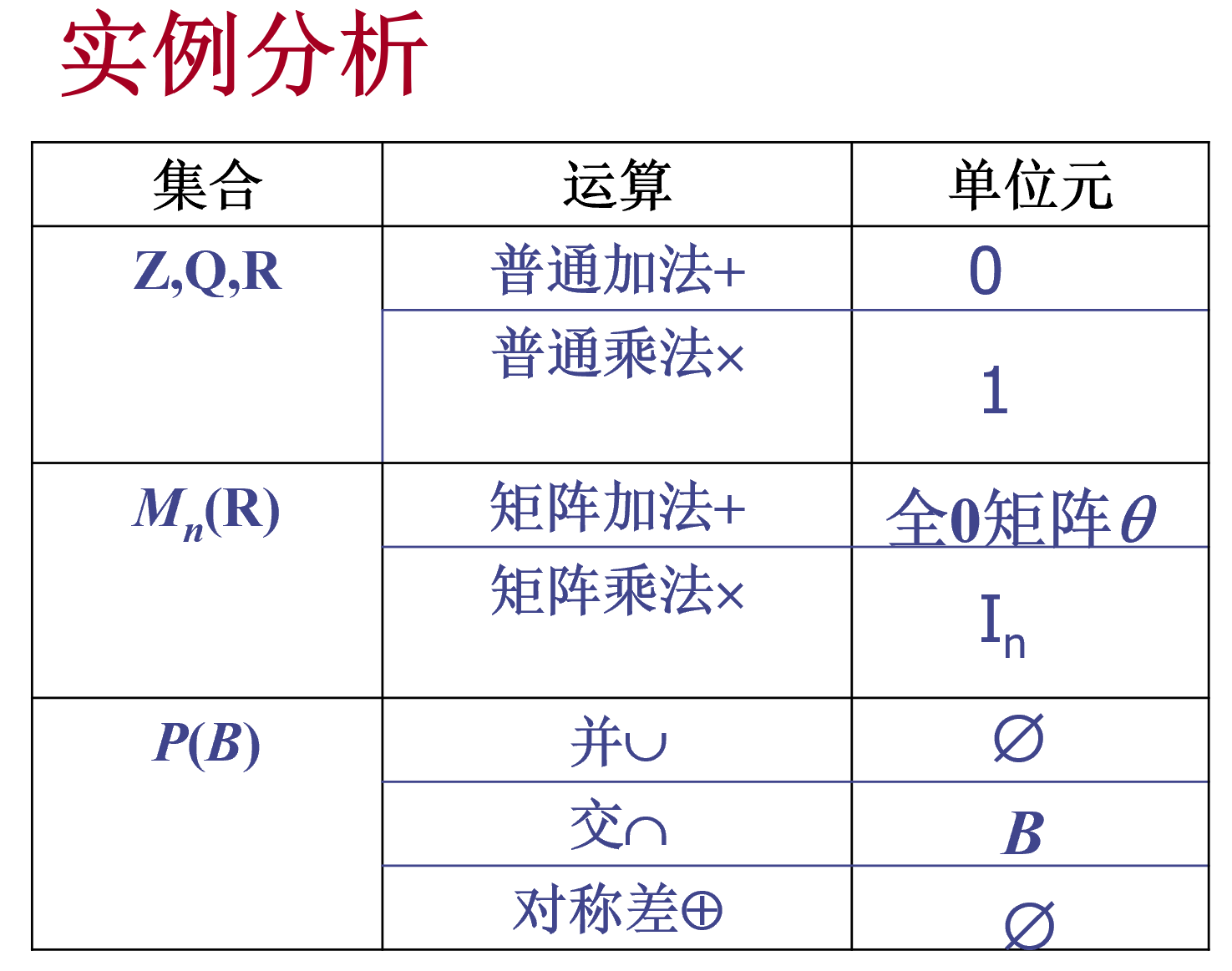
image-20210507144841767 image-20210507145126324
零元
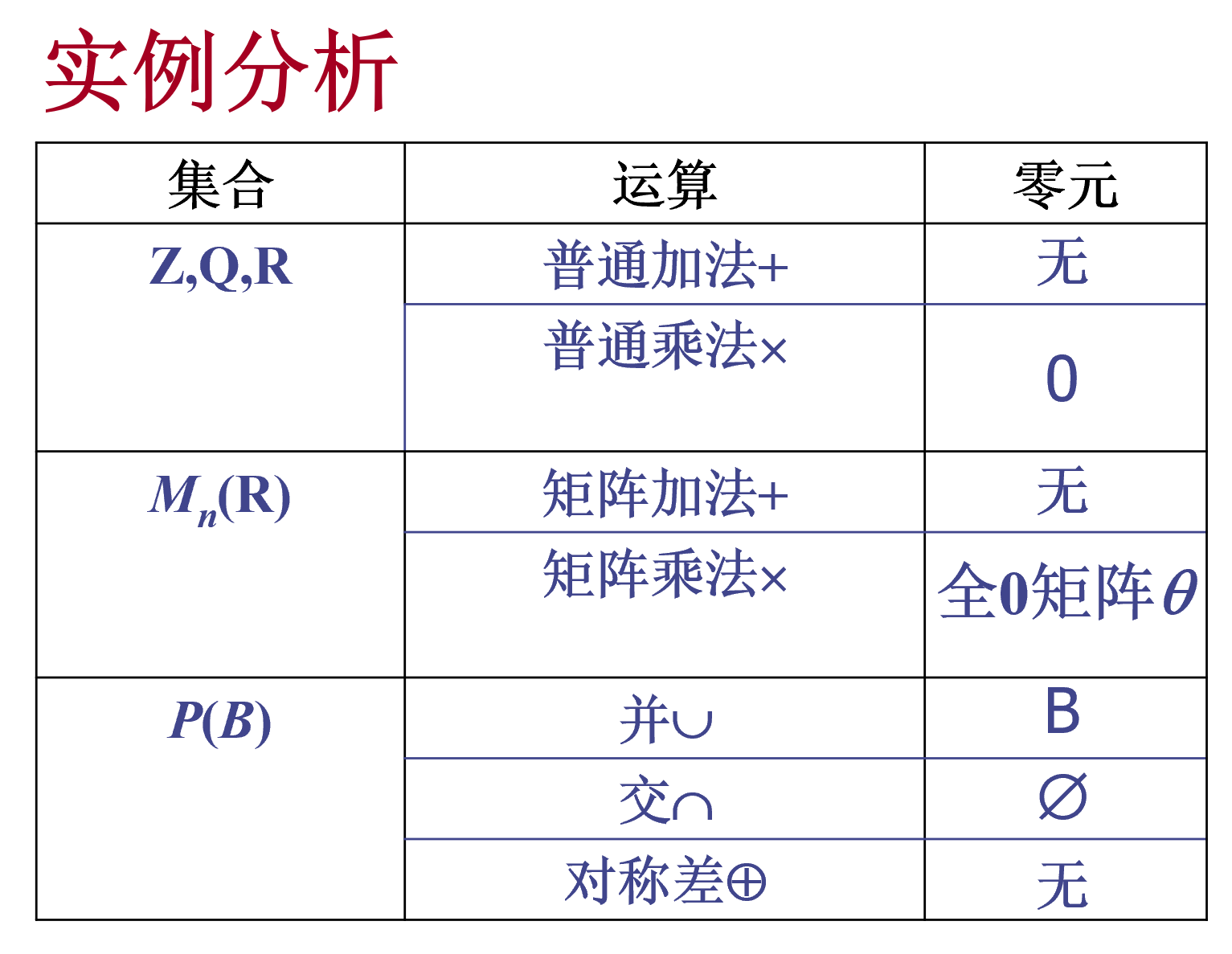
image-20210507144933840 image-20210507145043523
可逆元素及其逆元
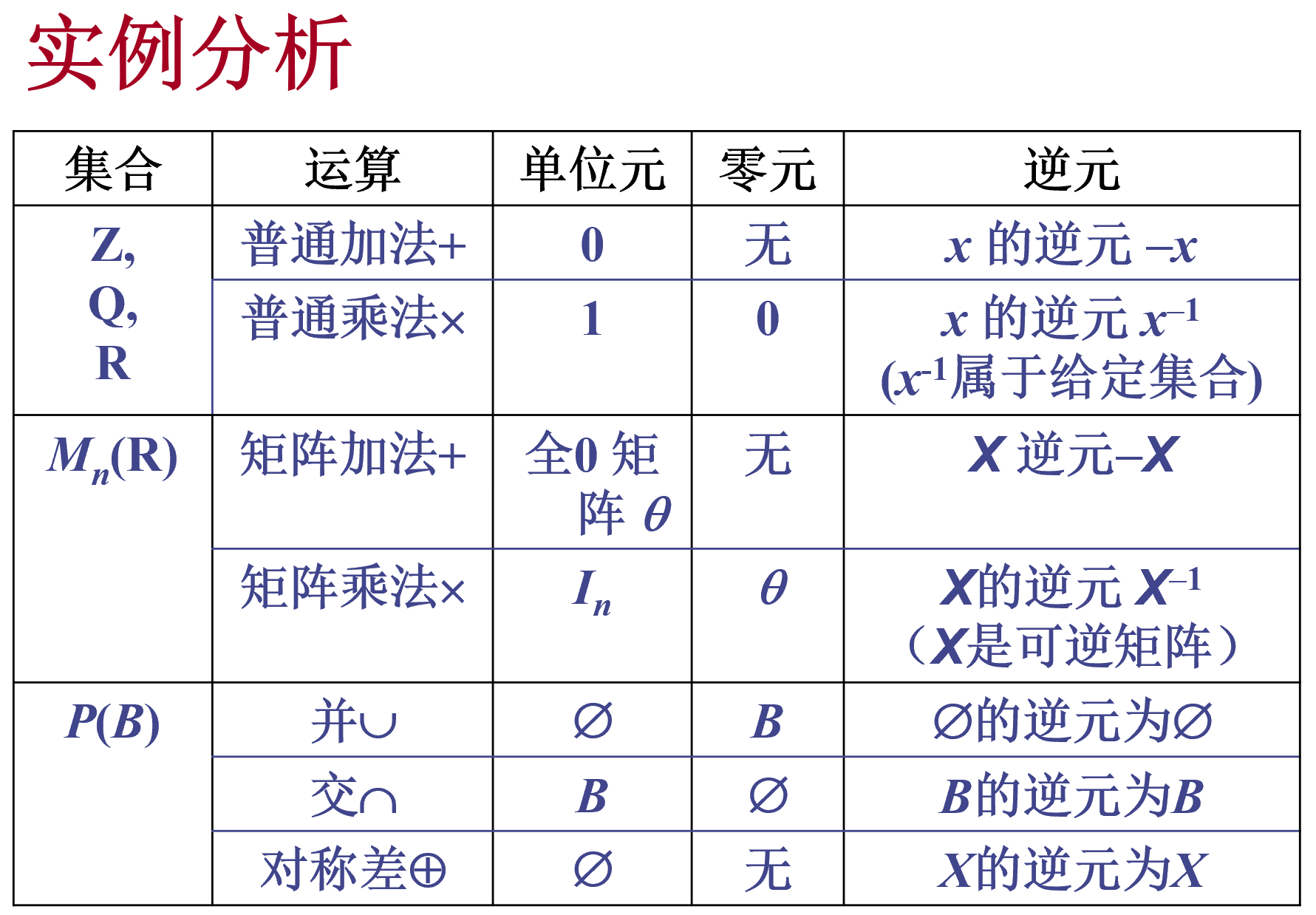
image-20210507145410131 image-20210507145453391

唯一性定理

当一个运算同时拥有左右单位元，其左右单位元必然相等

当一个运算同时拥有左右零元，其左右零元必然相等

当一个运算同时拥有左右逆元，其左右逆元必然相等

一个运算，可以有两个左单位元，但同时不可能再有右单位元。零元、逆元同理

image-20210507150822812 image-20210507150908440

消去律

封闭性、结合律、有单位元、有逆元，符合这四个条件的运算，即具有消去律

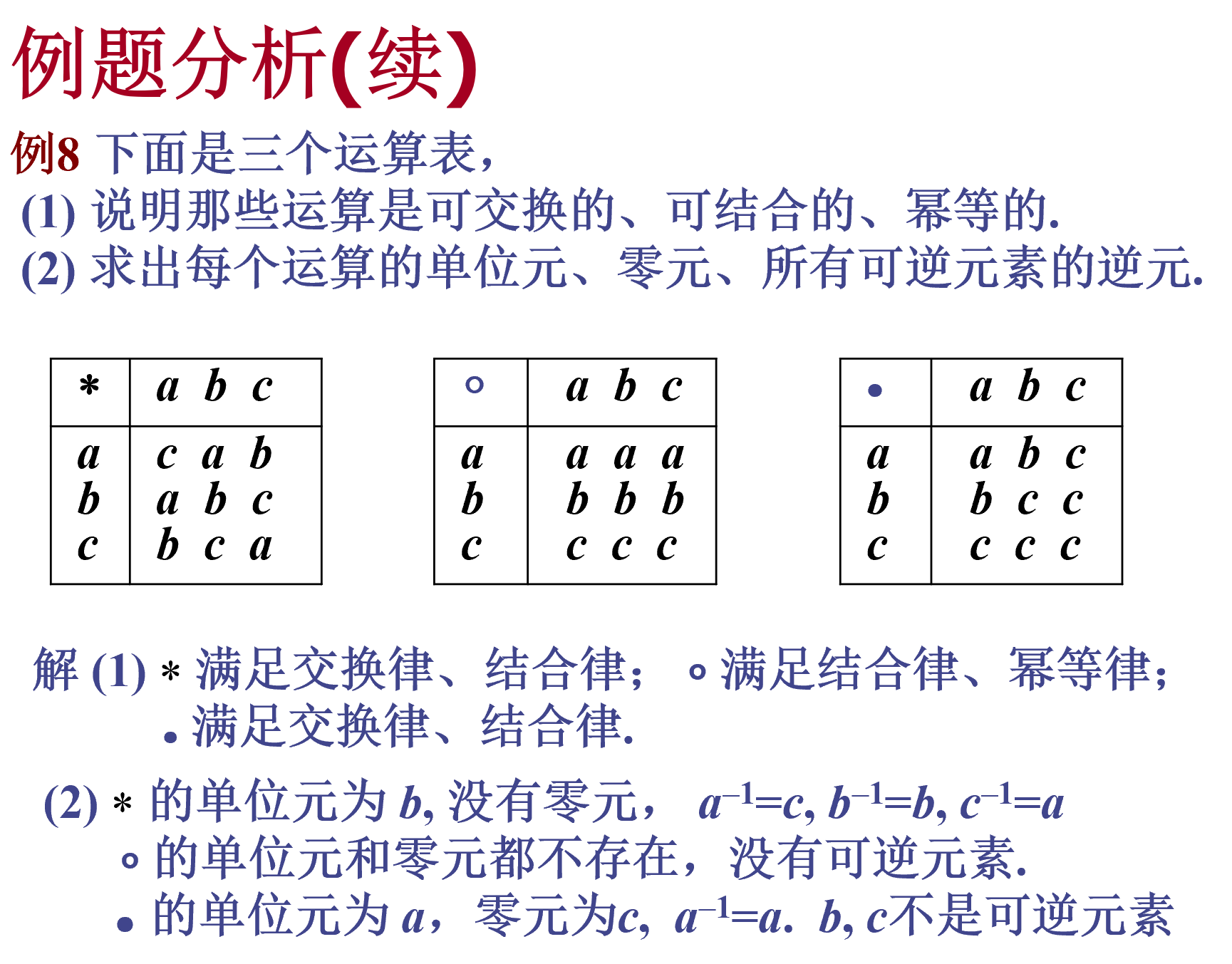
image-20210507150958159 image-20210507151024613 image-20210507151133256 image-20210507151155700

交换律看对称，结合律很麻烦，幂等律看对角线

单位元看行均为列值，零元看行列均为本身，逆元看表中为单位元的组合

代数系统

代数系统的定义与实例

定义
image-20210514141149452
实例
image-20210514141207509

代数系统的分类

image-20210514141307200 image-20210514141346301

公理系统 1（环）

  • 第一个运算有：结合律、单位元、逆元
  • 第二个运算：结合律
  • 第二运算对第一运算可分配

公理系统 3（域）

  • 第一个运算有：交换律、结合律、单位元、逆元
  • 非零元素全体对第二个运算：交换律、结合律、单位元、逆元
  • 第二运算对第一运算可分配

V~1~ 和 V~2~ 是环，V~3~ 不是环

V~1~ 是域

子代数系统

定义
image-20210514141407800
术语
image-20210514141430437
例
image-20210514141541245
意义
image-20210514141600673

积代数系统

定义

$\langle x_1,y_1\rangle \centerdot \langle x_1.y_2\rangle =\langle x_1\circ x_2,y_1*y_2\rangle$

image-20210514141614191

积代数可以推广到多个运算。

性质
image-20210514142206677 image-20210514142223522
意义
image-20210514142237347

代数系统的同态与同构

image-20210514142302324
同态映射的定义
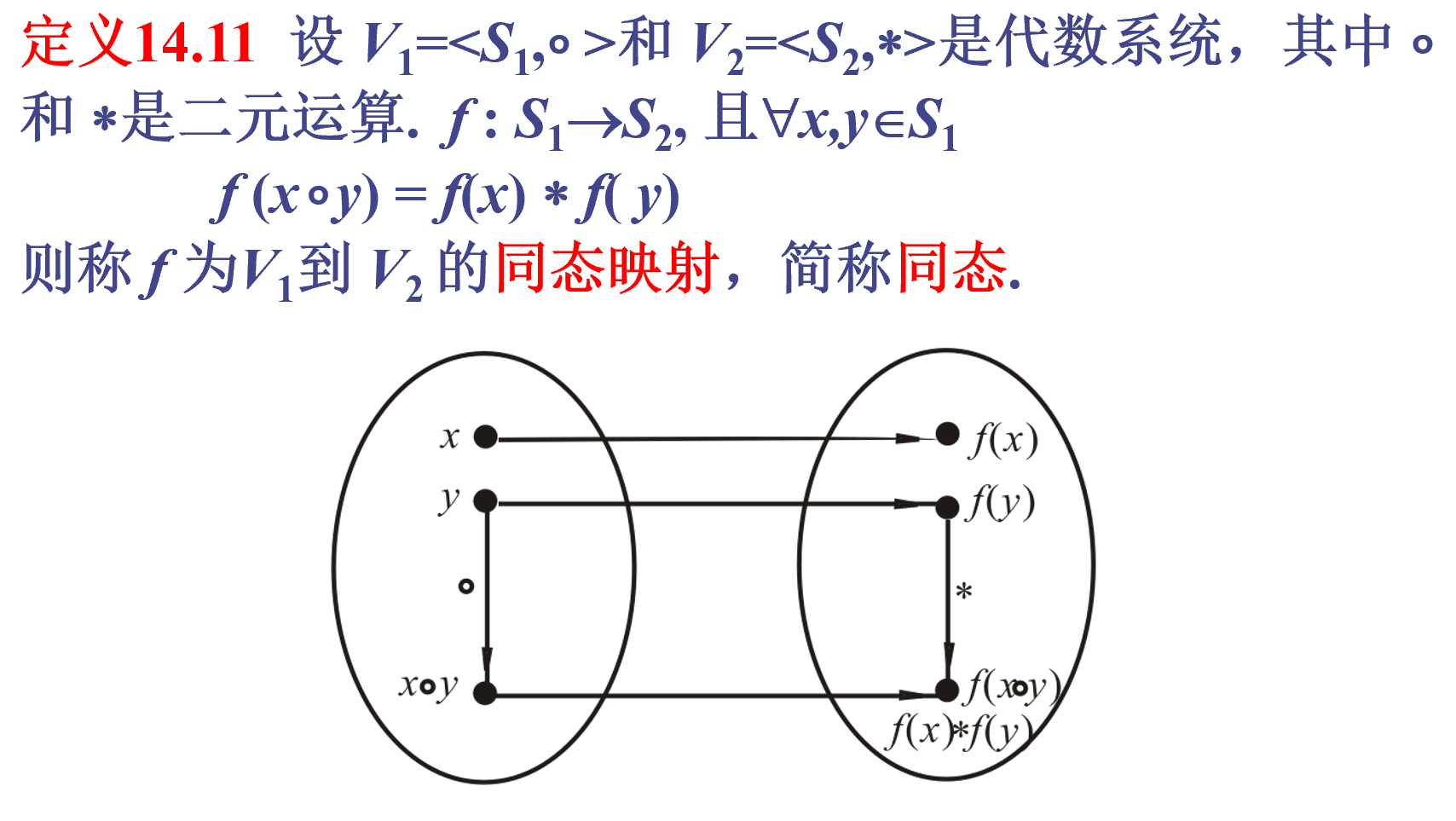
image-20210514153613761 image-20210514153720404
同态映射的分类
image-20210514153751793 image-20210514154107939 image-20210514154123242 image-20210514154136886
满同态映射的性质（意义）
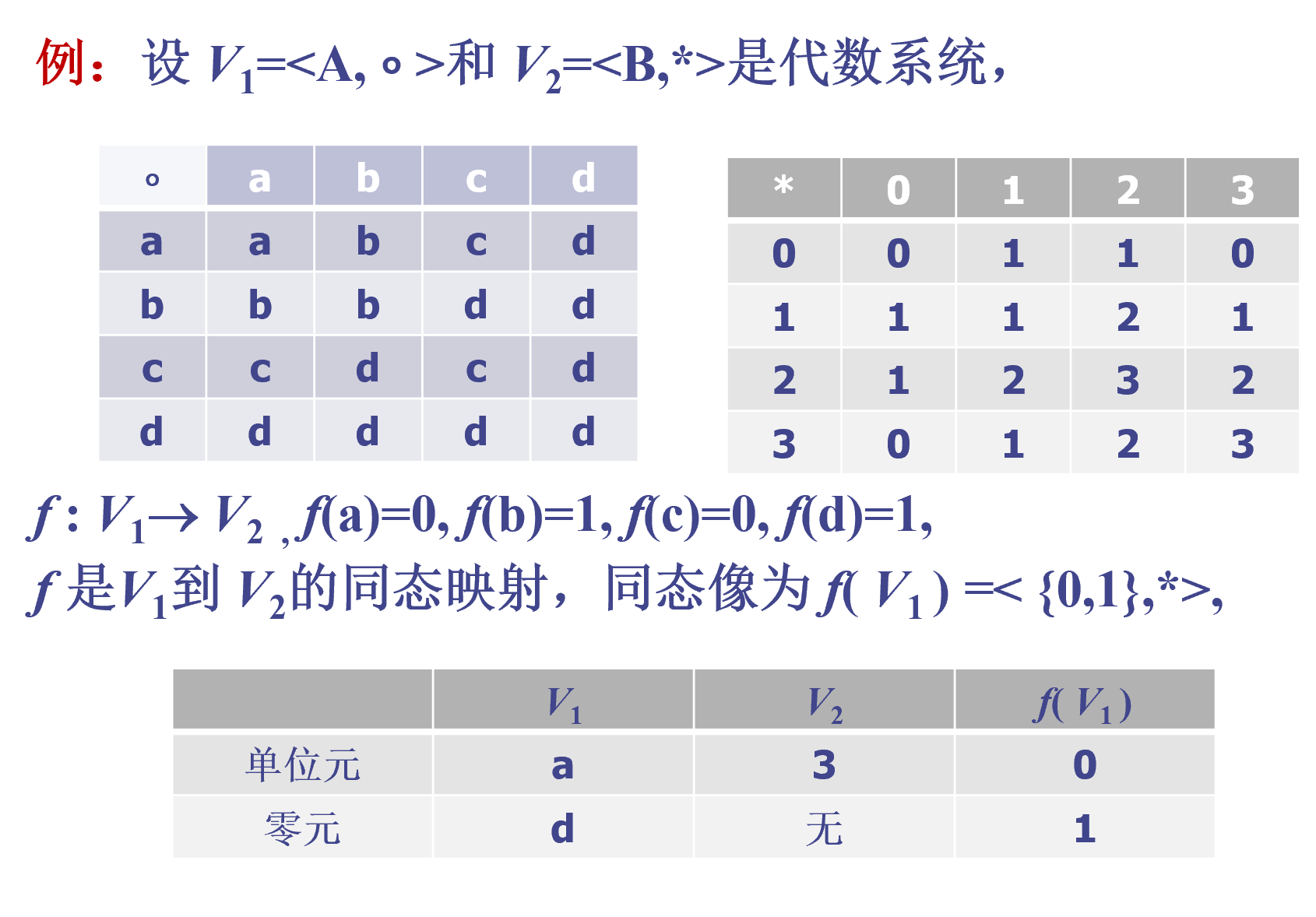
image-20210514154210769 image-20210514154225681 image-20210514154247113

几个典型的代数系统

入个门儿

半群与独异点

定义

半群：封闭性、结合律

独异点：封闭性、结合律、单位元

image-20210521141837812
实例
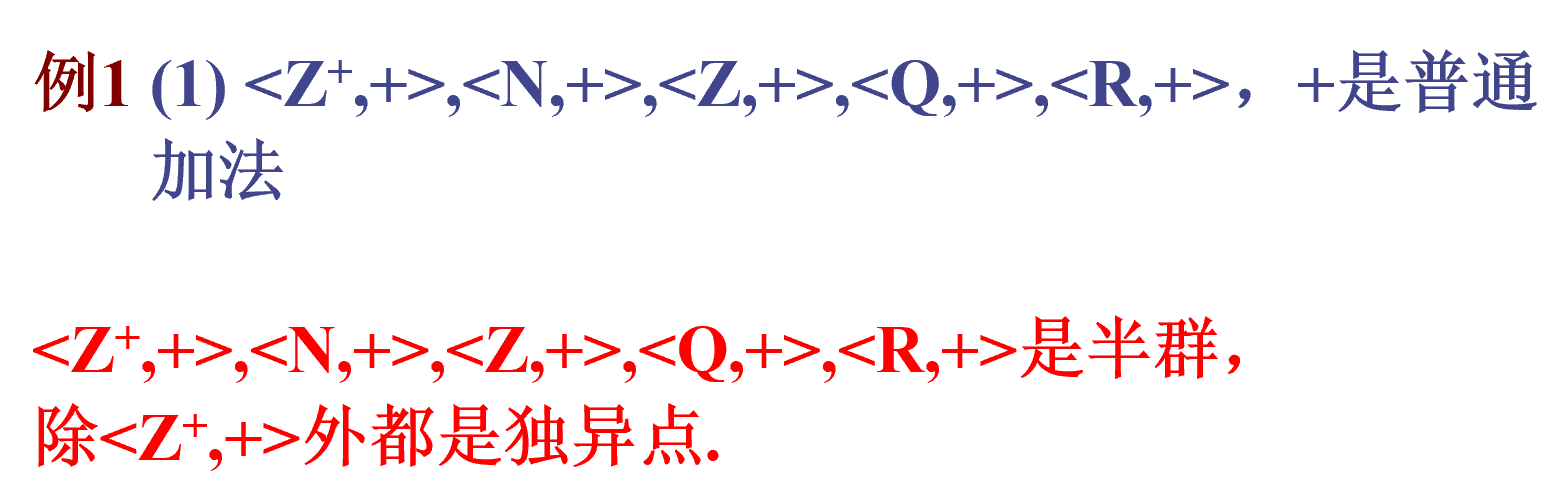
image-20210521141957386 image-20210521142006631 image-20210521142101265 image-20210521142117243 image-20210521142130750 image-20210521142141987
幂运算
image-20210521142216961
子代数

也叫子半群、子独异点

image-20210521142653189 image-20210521145026457
积代数

两个半群的积代数也是半群

两个独异点的积代数也是独异点

image-20210521145119483
同态
image-20210521145136543 image-20210521150837858

群

定义

封闭性、结合律、单位元、逆元

image-20210521151405970
实例
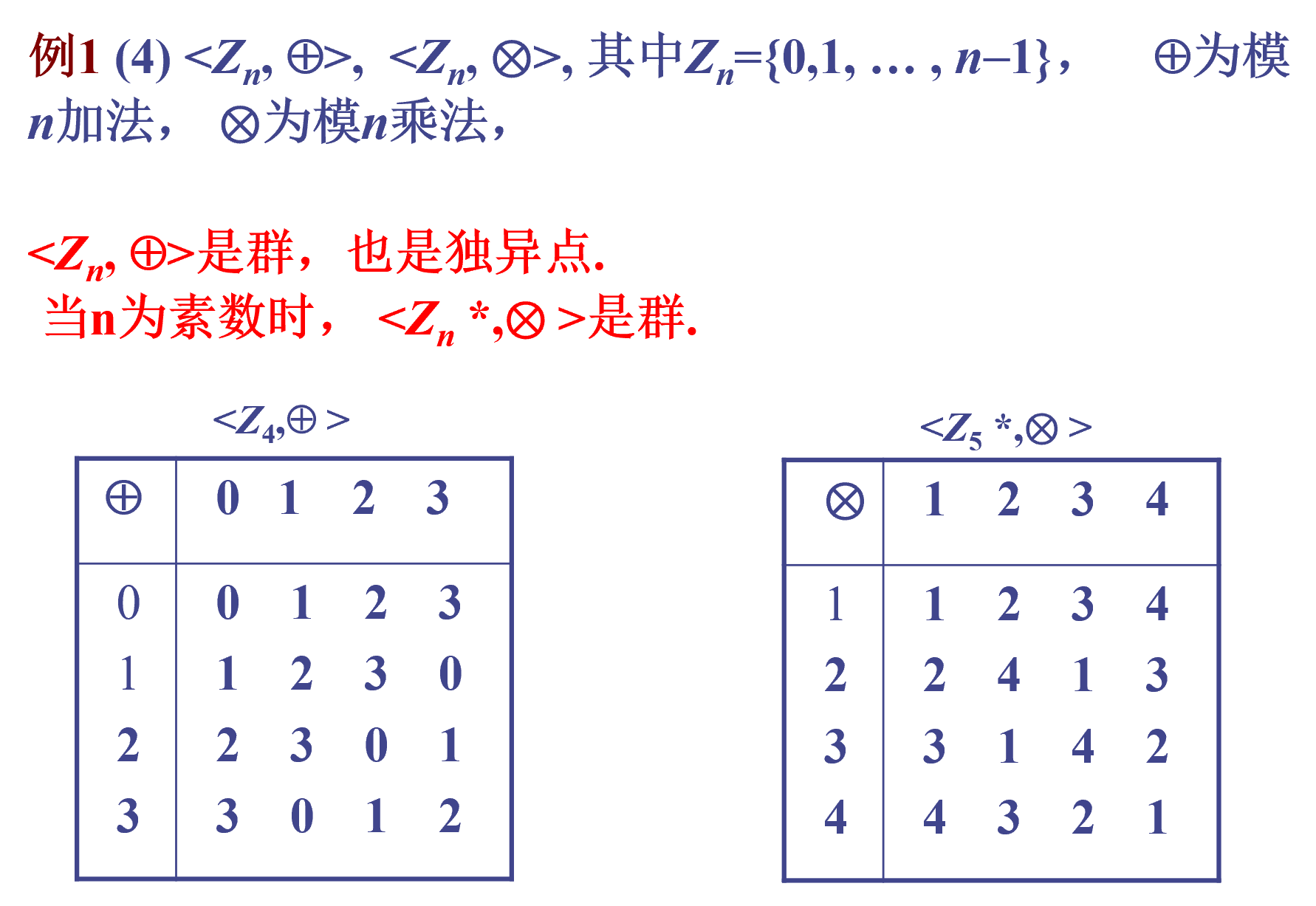
image-20210521151413690 image-20210521151429964 image-20210521151456255 image-20210521151509996 image-20210521160543871 image-20210521151525016 image-20210521160608359
术语
image-20210521151636890 image-20210521151655825 image-20210521151715515
性质
幂运算规则
image-20210528141954922
群方程存在唯一解
image-20210528141438352
消去律
image-20210528142045589 image-20210528142121941
群中元素阶的性质
image-20210528142210441
应用
image-20210528142358602 image-20210528142410772 image-20210528142418368
子群
定义
image-20210528142448062
判定定理

证明题必考

定理一：封闭性 + 逆元即可判定

image-20210528142511496 image-20210528142520144

定理二：定理一的合并

image-20210528142533342
重要子群的实例
image-20210528142556004 image-20210528142604799 image-20210528153007915
子群格

必考！

就是哈斯图

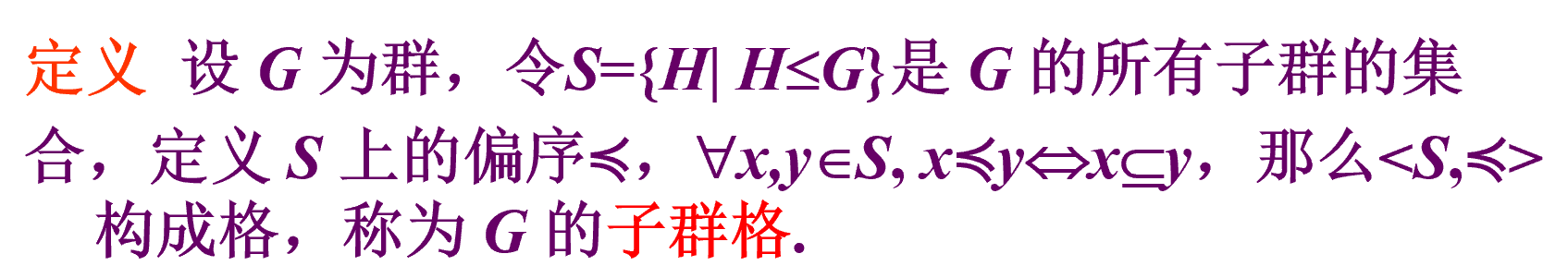
image-20210528153842171
同态与同构
同态的定义与分类
image-20210528154026671
群同态的性质
群同态的实例
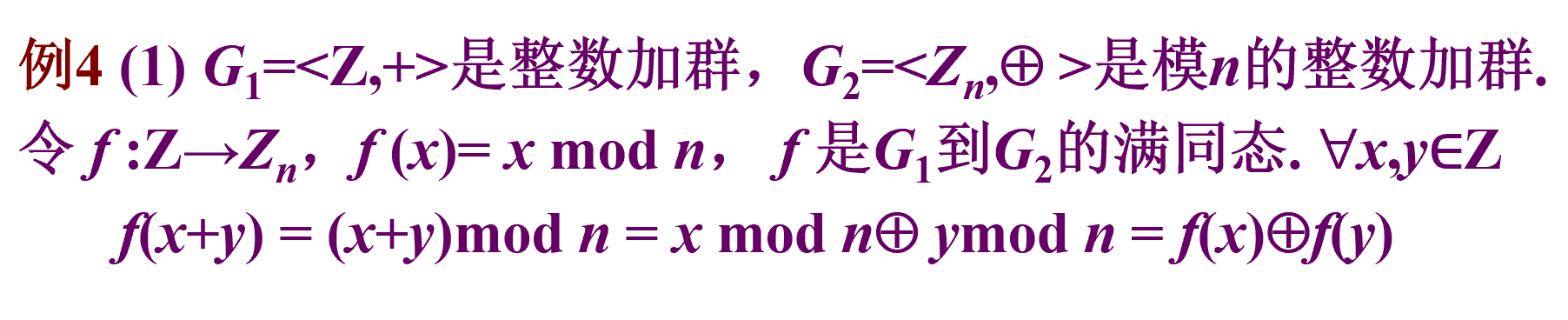
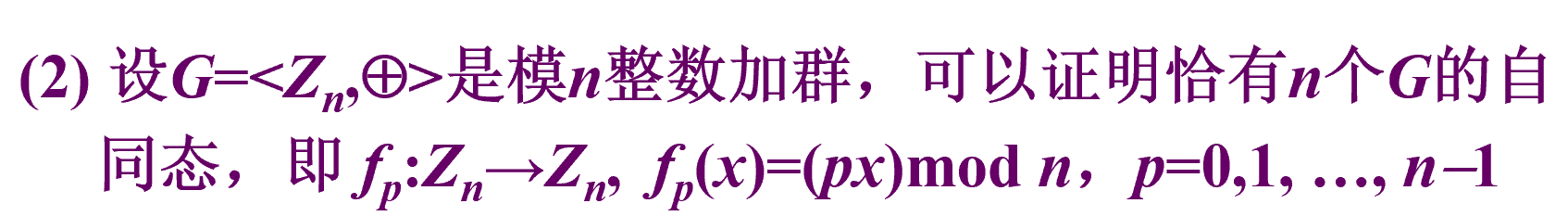
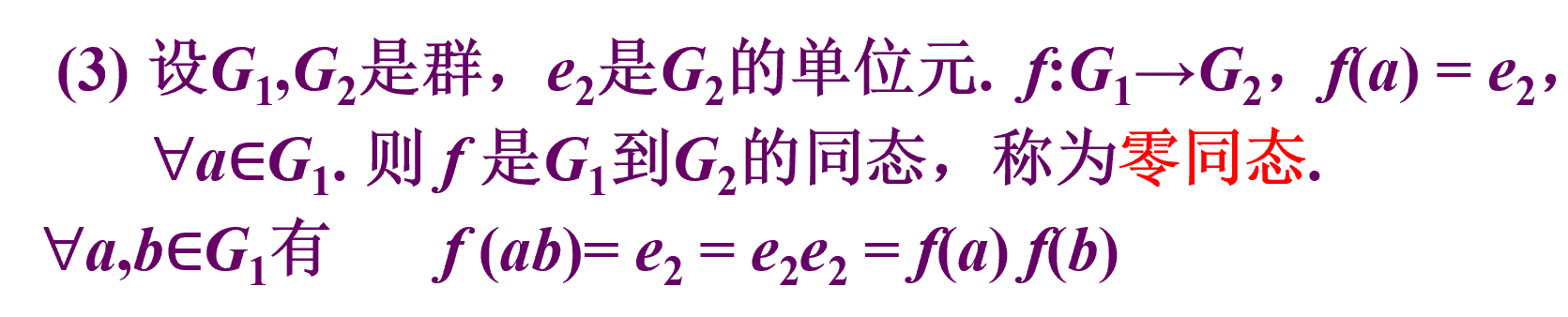
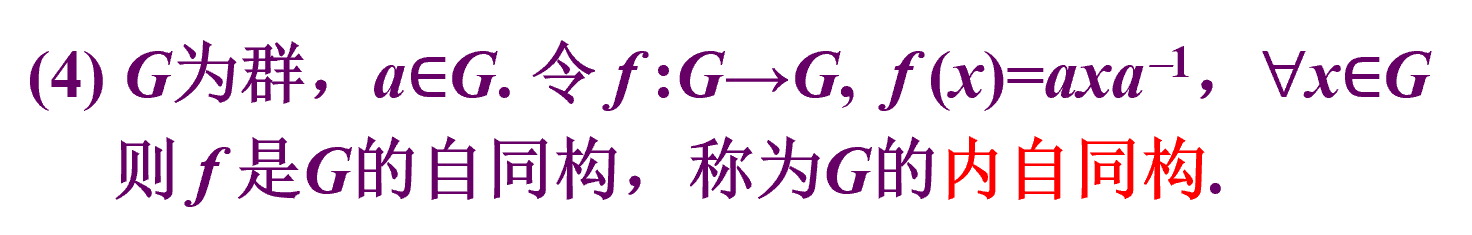
image-20210528162024512 image-20210528162031935 image-20210528162040420 image-20210528162047661 image-20210528162108912 image-20210528162209525
循环群

必考，大题写子群、子群格

定义

循环群可由生成元来生成

image-20210528162225846
分类

无限循环群：生成元的阶是无限阶

n 阶循环群：生成元的阶数为 n

循环群的生成元

无限循环群的生成元只有两个：a 和 a^-1^

n 阶循环群生成元的个数为：小于 n 且与 n 互素的整数 r 的个数；而且所有 a^r^ 都是 G 的生成元

image-20210528162322698
循环群的子群
image-20210604135943313 image-20210604135953030 image-20210604140002385
置换群

小题，考置换运算

n 元置换的定义

下图 $\sigma$ 也可以写成轮换 $\sigma=(134)(25)$

两个置换的乘积即函数的复合

image-20210604140144382
k 阶轮换与对换

  • 一阶轮换可以省略

  • 轮换几乎总是从 1 开始

image-20210604140433551

例：n 元置换分解为轮换

image-20210604140508587

例：求 (15236) (78) 的逆

(16325) (78)

分解为对换（不考）
image-20210604140527643
奇置换与偶置换
image-20210604140729154
n 元置换的乘法与求逆
image-20210604140814971
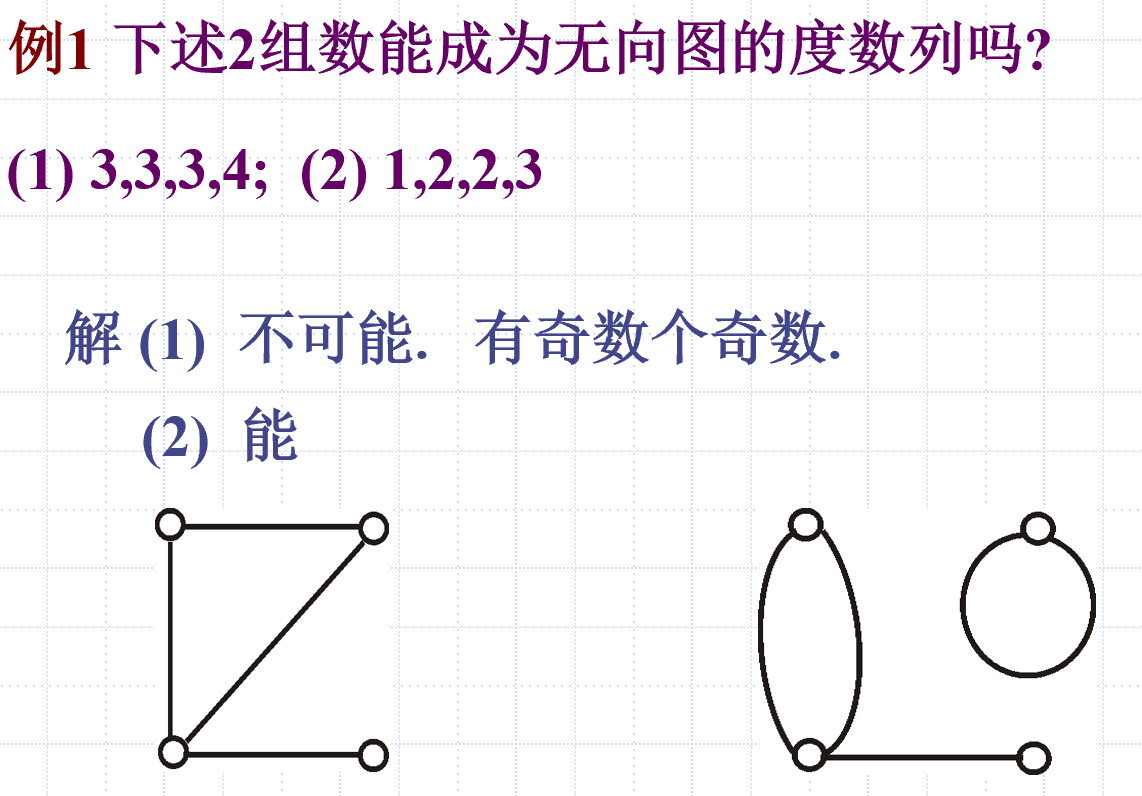
n 元置换群及其实例

n 元对称群的子群叫 n 元置换群

image-20210604140845515
S~3~ 的置换表
image-20210604140919968
更新于 2024-04-27
CC BY-NC 4.0
 离散数学
返回 | 主页