函数

函数的定义及性质

定义

函数的定义

设 $f$ 为二元关系，若对于任意 $x\in dom f$，都存在唯一的 $y\in ran f$，使得 $xfy$ 成立，则称 $f$ 为函数（或映射），这时也称 $y$ 为 $f$ 在 $x$的 值，记作 $y=f(x)$

函数相等

设$f,g$为函数，则 $$ f=g\Leftrightarrow f\subseteq g\land g\subseteq f $$ 根据上述定义，若$f$和$g$相等，一定满足下面两个条件

1. $domf=domg$，定义域相等
2. $\forall x\in domf=domg$ 都有 $f(x)=g(x)$，值相等

从A到B的函数

设$A,B$为集合，若 $$ f 为函数,domf=A,ranf\subseteq B $$ 则称$f$为从$A$到$B$的函数，记作$f:A\rightarrow B$

B上A

所有从$A$到$B$的函数的集合记作 $B^A$，符号化表示为 $$ B^A={f|f:A\rightarrow B} $$ 若 $|A|=m,|B|=n\quad m,n\neq 0$，则 $|B^A|=n^m$

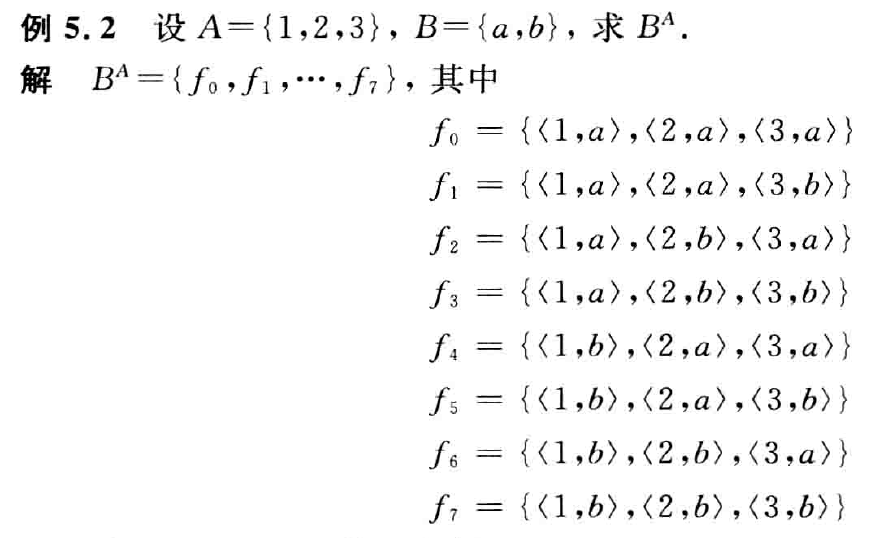
重要的函数实例

• 设 $f:A\rightarrow B$，若存在 $c\in B$ 使得对所有的 $x\in A$ 都有 $f(x)=c$，则称 $f:A\rightarrow B$ 是常函数

函数的像与完全原像

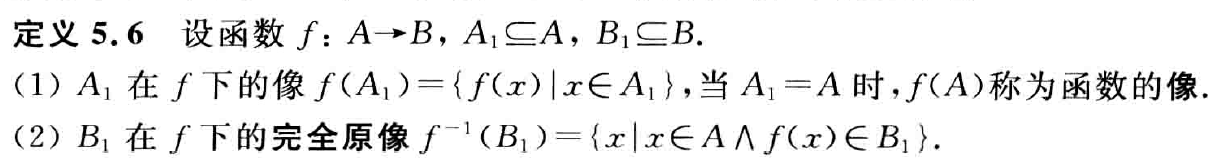
• 像：一些 $f(x)$ 的集合
• 完全原像：一些 $x$ 的集合

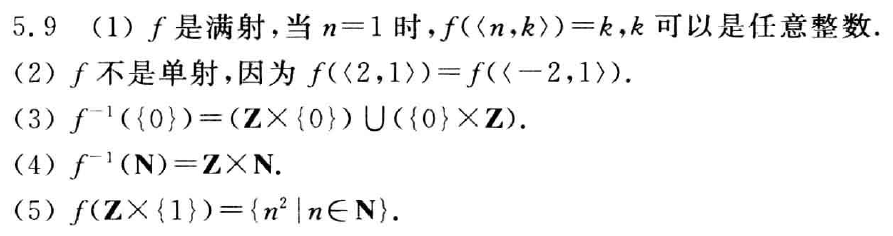
函数的==性质==

。满射：大家都有对象

。单射：一夫一妻

。双射：一夫一妻，大家都有对象

单射一定是单调的，满射的值域一定等于 $B$

函数的复合

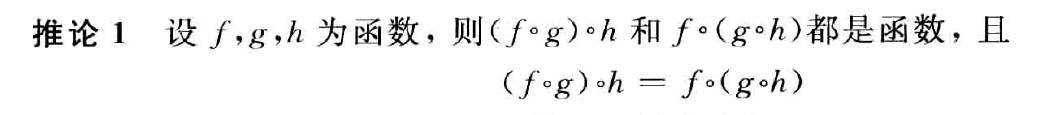
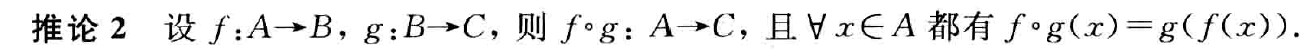
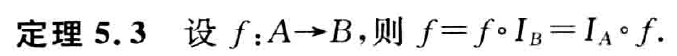
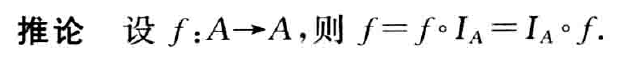
反函数