关系

关系的定义

有序对

两个元素按照一定次序构成的二元组称为一个有序对，记作 <x, y>​，区分第一元素和第二元素（即拥有有序性）

笛卡尔积

设 A，B 为集合，以 A 中元素作为第一元素，B 中元素为第二元素，构成的所有有序对叫做笛卡尔积，记为$A\times B$，即 $$ A\times B={<x,y>|x\in A\land y\in B} $$ 性质

• A，B 有空集时，笛卡尔积为空集

• 不适合交换律

• 不适合结合律

• 对于并或交运算满足分配律

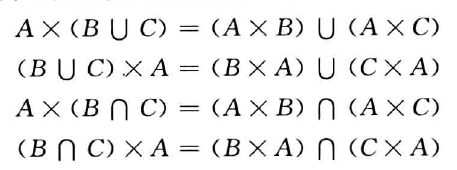
有序n元组和n阶笛卡尔积

$$ <x_1,x_2,\ldots,x_n> \ A_1\times A_2\times \ldots\times A_n={<x_1,x_2,\ldots,x_n>|x_i\in A_i} $$

二元关系

若集合满足以下条件之一：

1. 集合非空，它的元素都是有序对
2. 集合是空集

则该集合是一个二元关系，简称关系，记作$R$

如$<x,y>\in R$，可记作$xRy$；如$<x,y>\notin R$，可记作$x\not Ry$

例

从 $A$ 到 $B$ 的二元关系

$A\times B$ 的任何自己所定义的二元关系叫做从 $A$ 到 $B$ 的二元关系，当 $A=B$ 时则叫做$A$上的二元关系

。==从 $A$ 到 $B$ 的二元关系近似看作 $A\times B$ 的子集==

例

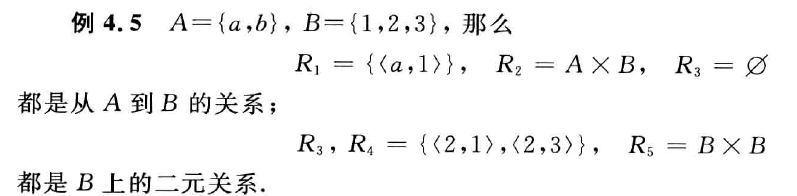
关系的重要实例

全域关系

$$ E_A={\langle x,y\rangle|x\in A\land y\in A}=A\times A $$

恒等关系

$$ I_A={\langle x,x\rangle|x\in A} $$

小于等于关系

$$ L_A={\langle x,y\rangle|x,y\in A\land x<y}\qquad A\subseteq R $$

整除关系

$$ D_A={\langle x,y\rangle|x,y\in A\land x 整除 y} \qquad B\subseteq Z^* $$

包含关系

$$ R_{\subseteq}={\langle x,y\rangle|x,y\in A\land x\subseteq y} $$

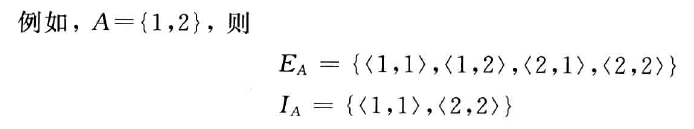
关系的表示

关系的集合表达式

懂的都懂

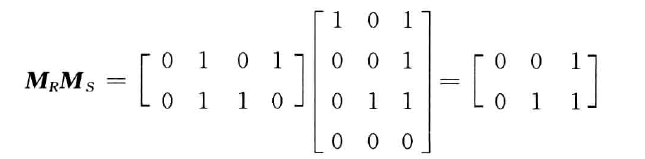
关系矩阵

设$R$是从$A$到$B$的关系，$R$ 的关系矩阵是布尔矩阵$M_R=(r_{ij}){m\times n}$，其中$r{ij}=1\Leftrightarrow \langle x_i,y_j\rangle\in R $

关系图

$R$的关系图是$G_R=\langle A,R\rangle$，其中 A 为 G 的节点集

关系的运算

基本运算

域

• 定义域：第一元素的集合，$domR$
• 值域：第二元素的集合，$ranR$
• 域：全体元素的集合，$fldR$

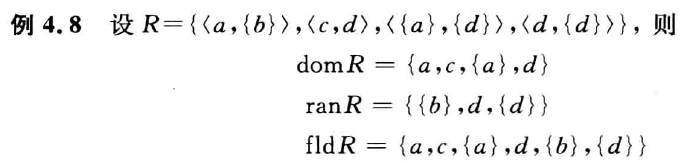
逆

$$ R^{-1}={\langle y,x\rangle|\langle x,y\rangle\in R} $$

• 小于关系的逆是大于关系
• 整数关系的逆是倍数关系

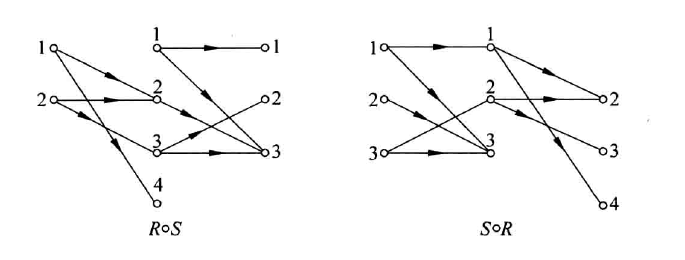
合成运算

$$ R\circ S={\langle x,z\rangle|\exists y(\langle x,y\rangle\in R\land\langle y,z\rangle\in S)} $$

• 定理 1：设$F$是任意的关系，则

  • $(F^{-1})^{-1}=F$
  • $domF^{-1}=ranF,ranF^{-1}=domF$

• 定理 2：设$F,G,H$是任意的关系，则

  • $(F\circ G)\circ H=F\circ(G\circ H)$
  • ==$(F\circ G)^{-1}=G^{-1}\circ F^{-1}$==

• 定理 3：设$R$为$A$上的关系，则

  • $R\circ I_A=I_A\circ R=R$

幂运算

定义

设$R$为$A$上的关系，则$R$的 n 次幂的定义为

1. $R^0={\langle x,x\rangle|x\in A}=I_A$
2. $R^{n+1}=R^n\circ R$

定理

• 设$A$为$n$元集，$R$为$A$上的关系，则存在自然数 s 和 t，使得 $R^s=R^t$
• 设$R$为$A$上的关系，有
  • $R^m\circ R^n=R^{m+n}$
  • $(R^{m})^n=R^{mn}$
• 设$R$为$A$上的关系，若存在自然数 s 和 t$(s<t)$，使得$R^s=R^t$，则
  • 对任何$k\in N$有$R^{s+k}=R^{t+k}$
  • 对任何$k,i\in N$ 有 $R^{s+kp+i}=R^{s+i}$，其中 $p=t-s$
  • 令$S{R^o,R^1,\ldots,R^{t-1}}$，则对于任意的$q\in N$有$R^q\in S$

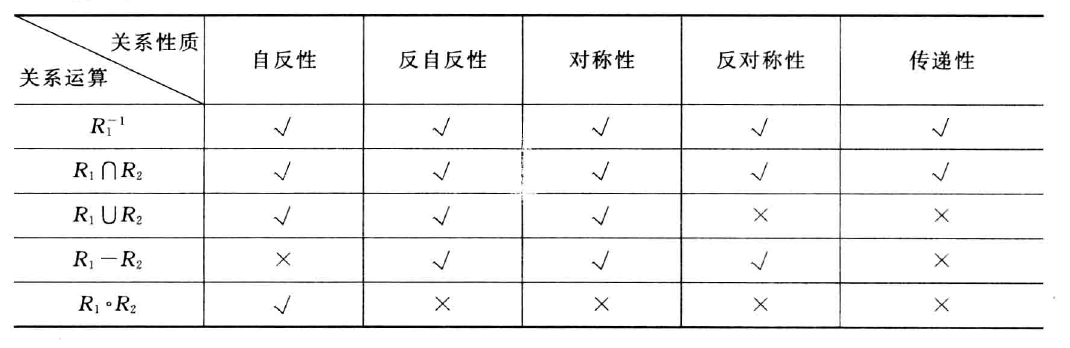
关系的性质

定义及判别

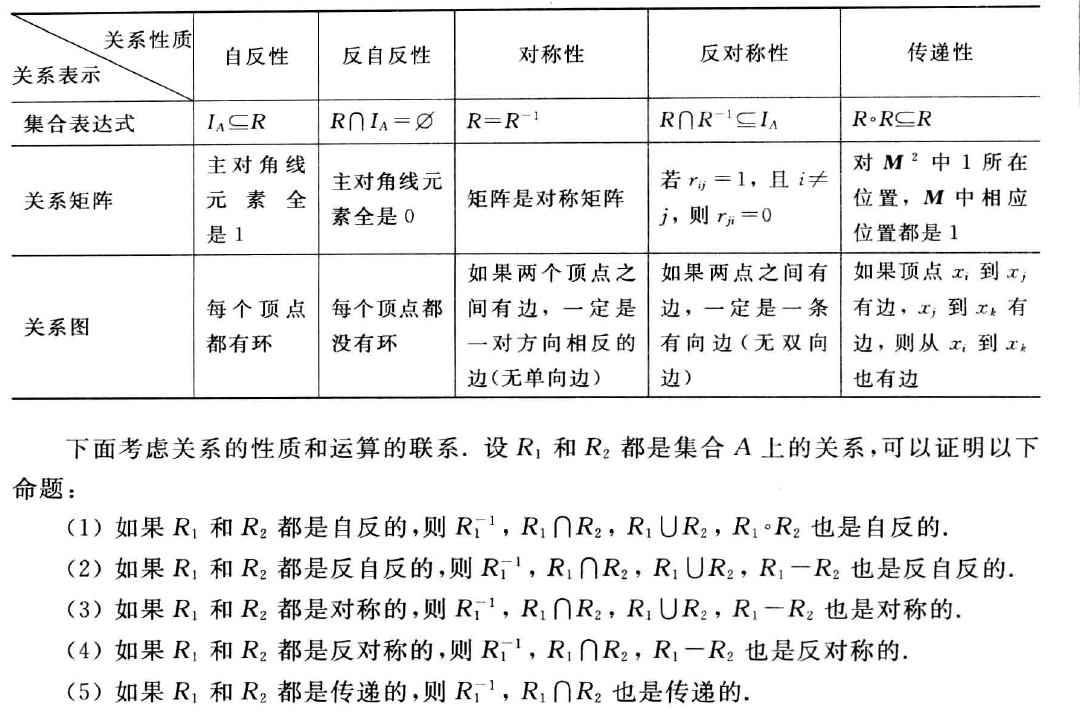
自反

设$R$为$A$上的关系，有

• 若$\forall x(x\in A\rightarrow\langle x,x\rangle \in R)$，则称$R$在$A$上自反
• 若$\forall x(x\in A\rightarrow\langle x,x\rangle \notin R)$，则称$R$在$A$上反自反

自反：对角线全为 1

反自反：对角线全为 0

除空关系外，一个关系不可能同时是自反和反自反的

对称

设$R$为$A$上的关系，有

• 若 $\forall x\forall y(x,y\in A\ \land\langle x,y\rangle \in R\rightarrow \langle y,x\rangle\in R)$，则称$R$在$A$上对称
• 若 $\forall x\forall y(x,y\in A\ \land\langle x,y\rangle \in R\land \langle y,x\rangle\in R\rightarrow x=y)$，则称$R$在$A$上反对称

对称：每个元素要么自我相等要么两两相反

反对称：每个元素不能两两相反（但可以自我相等）

一个关系可以同时是对称和反对称的

传递

设$R$为$A$上的关系，有 $$ \forall x\forall y\forall z(x,y,z\in A\land \langle x,y\rangle\in R\land \langle y,z\rangle\in R\rightarrow \langle x,z\rangle\in R) $$ 则称$R$是传递的

判别

关系的闭包

设$R$为$A$上的关系，若$R$不具有某种性质，可以通过在$R$中加入最少数量的有序对来补充$R$，使其具有某种性质

定义

设$R$为非空集合$A$上的关系，$R$的自反（对称或传递）闭包是$A$上的关系$R’$，使$R’$满足以下条件

• $R’$是自反的（对称的或传递的）
• $R\subseteq R'$
• 对$A$上任何包含$R$的自反（对称或传递）关系$R’’$有$R’\subseteq R’'$

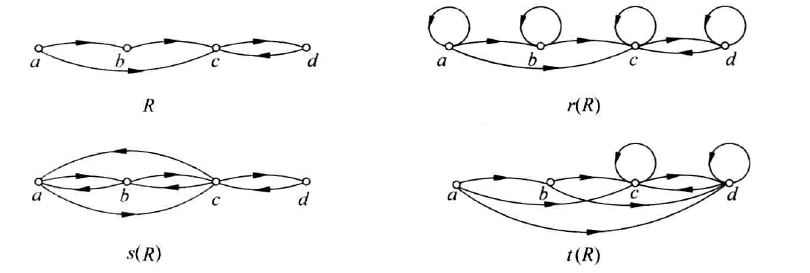
自反闭包：$r(R)$

对称闭包：$s(R)$

传递闭包：$t(R)$

理解

想使一个关系拥有某一性质，向其中尽量少地添加一些有序对，形成的新关系称为闭包。

定理

设$R$为$A$上的关系，有

• $r(R)=R\cup R^0$
• $s(R)=R\cup R^{-1}$
• $t(R)=R\cup R^2\cup R^3\cup\ldots$

用矩阵关系表示

• $M_r=M+E$
• $M_S=M+M'$
• $M_t=M+M^2+M^3+\ldots$

用图关系表示

• $G_r$：在图$G$中每一个缺少环的结点都加一个环
• $G_s$：将$G$中的单向边变成双向边
• $G_t$：

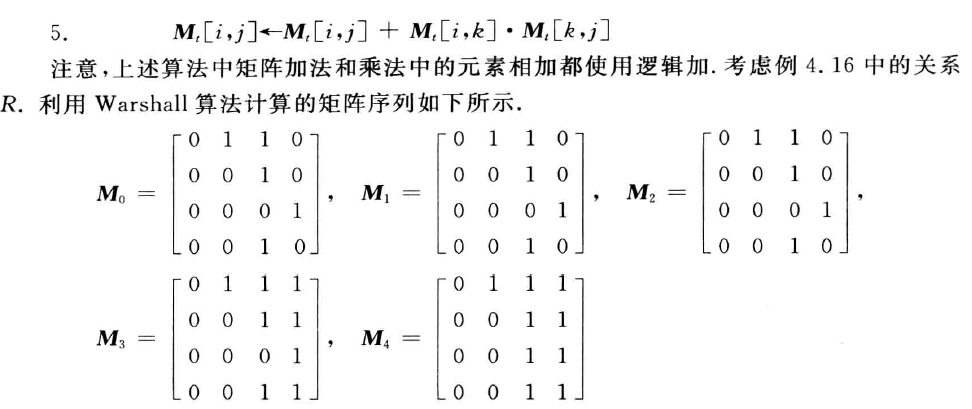
WarShall算法

例

等价关系与偏序关系

等价关系

设$R$为非空集合$A$上的关系，若$R$是自反的，对称的，传递的，则称$R$为$A$上的等价关系，

对于任何元素 $x,y\in A$，若$xRy$，则称 x, y 等价，记为$x\sim y$

等价类和商集

定义

按某一等价关系，将 A 的元素划分成若干个子集，彼此等价的元素被分在同一个子集里，这些子集称作这个等价关系产生的等价类。记作$[x]$

性质

• $\forall x\in A,[x]$是$A$的非空子集
• $\forall x,y\in A$，如果$xRy$，则$[x]=[y]$
• $\forall x,y\in A$，如果$xRy$不成立，则$[x]$与$[y]$不交
• $\bigcup_{x\in A}[x]=A$，即$A$中元素构成的所有等价类的并集等于$A$

商集

$A$上的全体等价类构成的集合称作$A$关于等价关系$R$的商集，记作$A/R$，即 $$ A/R={[x]_R|x\in A} $$

集合的划分

定义

设$A$为非空集合，若$A$的子集族 $\pi(\pi\subseteq P(A))$满足下面条件

1. $\emptyset\notin\pi$（无空集）
2. $\forall x\forall y(x,y\in\pi\land x\neq y\rightarrow x\cap y=\emptyset)$（元素无公共部分）
3. $\bigcup_{x\in\pi}x=A$（拼起来是完整的）

则$\pi$称是$A$的一个划分，称$\pi$中的元素为$A$的划分块

• 商集$A/R$就是$A$的一个划分，所以又可以定义商集$R$

$$ R={\langle x,y\rangle|x,y\in A\land x 与 y 在\pi 的同一划分块中 } $$

偏序关系

非空集合$A$上的自反、反对称和传递的关系称为$A$上的偏序关系，简称偏序，记作$\preceq$

若$\langle x,y\rangle\in\preceq$，则记作$x\preceq y$，读作 x “小于等于” y​

可比

设 $R$ 为非空集合 $A$ 上的偏序关系，$\forall x,y\in A$，若$x\preceq y\lor y\preceq x$，则称 x 与 y 可比

拟序

设$R$为非空集合$A$上的偏序关系，若$R$是反自反的和传递的，则称$R$是$A$上的拟序关系，简称为拟序，记作$\prec$

全序

设$R$为非空集合$A$上的偏序关系，$\forall x,y\in A$，x 与 y 都是可比的，则称$R$为全序关系，简称全序（或线序）

覆盖

设$R$为非空集合$A$上的偏序关系，$\forall x,y\in A$，若$x\prec y$且不存在$z\in A$使得$x\prec z\prec y$，则称 y覆盖x​

定义偏序关系$R$的一个子关系——覆盖关系$T$ $$ T={\langle x,y\rangle|\langle x,y\rangle\in R 且 y 覆盖 x} $$ $T$的自反传递闭包$rt(T)$就等于$R$

偏序集

集合$A$和$A$上的偏序关系$\preceq$一起叫做偏序集，记作$\langle A,\preceq\rangle$

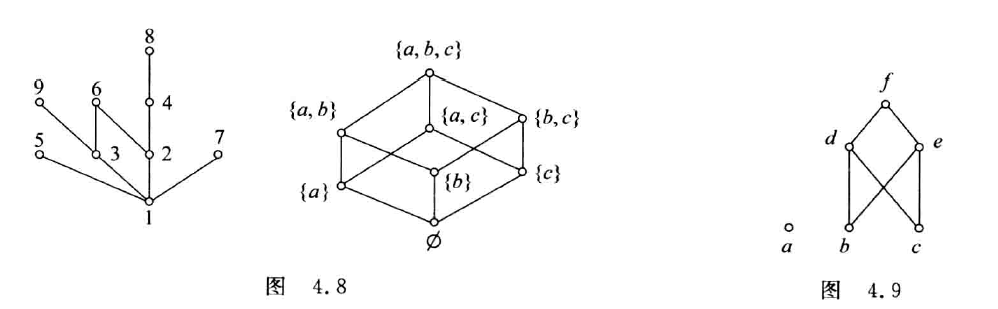
哈斯图

定义

利用偏序自反、反对称、传递性简化的关系图

特点

• 每个结点没有环
• 两个联通结点之间的序关系通过结点位置的高低表示，位置低的元素顺序在前
• 具有覆盖关系的两个结点之间连边

特殊元素或子集

设$\langle A,\preceq\rangle$为偏序集，$B\subseteq A,y\in B$

• 若$\forall x(x\in B\rightarrow y\preceq x) $成立，则称$y$为$B$的最小元
• 若$\forall x(x\in B\rightarrow x\preceq y) $成立，则称$y$为$B$的最大元
• 若$\forall x(x\in B\land x\preceq y\rightarrow x=y) $成立，则称$y$为$B$的极小元
• 若$\forall x(x\in B\land y\preceq x\rightarrow x=y) $成立，则称$y$为$B$的极大元

有性质如下

• 对于有穷集，极小元和极大元一定存在，还可能存在多个
• 最小元和最大元不一定存在，如果存在一定唯一
• 最小元一定是极小元，最大元一定是极大元
• 孤立结点既是极小元，也是极大元

设$\langle A,\preceq\rangle$为偏序集，$B\subseteq A,y\in A$

• 若$\forall x(x\in B\rightarrow x\preceq y) $成立，则称$y$为$B$的上界
• 若$\forall x(x\in B\rightarrow y\preceq x) $成立，则称$y$为$B$的下界
• 令$C={y|y 为 B 的上界}$，则称$C$的最小元为$B$的最小上界或上确界
• 令$D={y|y 为 B 的下界}$，则称$D$的最大元为$B$的最大下界或下确界

有性质如下

• 上界，下界，最大下界，最小上界不一定存在
• 如果下界，上界存在，也不一定是唯一的
• 最大下界，最小上界如果存在，则是唯一的
• 子集$B$的最小元就是他的最大下界，最大元就是他的最小上界；反之不对

理解

最小元素就是在子集中处于最低层且每个元素通过图中路径都可以找到它且它的下面没有元素。

极大元素就是在子集中它的上面没有元素。

极小元素就是在子集中它的下面没有元素。

（记住：这里如果是子集，应当将子集当成一个单独的整体，而不受全集的影响。）

上届：所有子集内的元素沿着路径向上都可以找到的元素（这里包括子集和子集以外的元素）。根据上面所说的话，我们可以断定上届也可以是子集内的元素。

下届：所有子集内的元素沿着路径向下都可以找到的元素（这里包括子集和子集以外的元素）。根据上面所说的话，我们可以断定下届也可以是子集内的元素。

上确界：这里我们可以将上届元素看成一个独立的整体，而上确界就是这个集合的最小元，我们称为最小上届。根据上面所说的话，我们可以断定上届也可以是上确界。

下确界：这里我们可以将下届元素看成一个独立的整体，而下确界就是这个集合的最大元，我们称为最大下届。根据上面所说的话，我们可以断定下届也可以是下确界。

特殊子集

设$\langle A,\preceq\rangle$为偏序集，$B\subseteq A$

• 若$\forall x,y\in B$，$x$与$y$都是可比的，则称$B$是$A$中的一条链，$B$中的元素个数称为链的长度。
• 若$\forall x,y\in B,x\neq y$，$x$与$y$都是不可比的，则称$B$是$A$中的一条反链，$B$中的元素个数称为反链的长度。

有定理

• 设$\langle A,\preceq\rangle$为偏序集，若$A$中最长链的长度为$n$，则该偏序集可以分解为$n$条不相交的反链