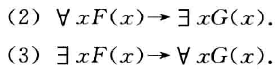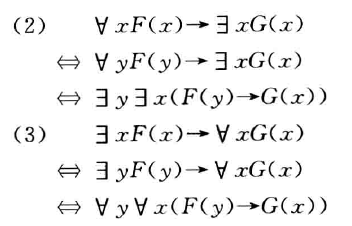一、数学语言与证明方法

符号

• 运算
  • $A-B$：B 对 A 的相对补
  • $A\oplus B$：A 与 B 的对称差 A 与 B 中不重叠的部分
  • ~$A$：绝对补，等于$E-A$
  • $P(A)$：A 的幂集（A 的所有子集组成的集合）
    • $|P(A)|=\sum\limits_{i=1}^n C_n^i \quad (n=|A|)$
  • $a\mid b$：a 整除 b
  • $a\nmid b$：a 不能整除 b
  • $a\equiv b(mod \ n)$：a 与 b 被 n 除余数相同
  • $(a-b)\equiv 0(mod \ n)$：等价于$n\mid (a-b)$
  • $\lceil x\rceil$：大于等于 x 的最小整数
  • $\lfloor x\rfloor$：小于等于 x 的最大整数
• 集合
  • $|A|$：A 中元素的个数
  • $N$：自然数集
  • $Z$：整数集
  • $Q$：有理数集
  • $R$：实数集
  • $C$：复数集
• 逻辑
  • $p\rightarrow q$：如果 p，则 q
  • $p\leftrightarrow q$：当且仅当 q 与 q 同时为真或同时为假
  • $A\Rightarrow B$：表示$A\rightarrow B$恒真，若 A 真，则 B 一定真
  • $A\Leftrightarrow B$：$p\leftrightarrow q$恒真，A 与 B 要么同时为真，要么同时为假

集合

规律

• $A\oplus A=\empty$

• $\cap$对$\oplus$的分配律：$A\cap (B\oplus C)=(A\cap B)\oplus (A\cap C)$

• $\oplus$对$\cap$没有分配律

• $\oplus$的消去律：$A\oplus B=A\oplus C\Rightarrow B=C$

证明集合包含或相等

1. 根据定义证明（等式两边互为子集），通常取元素$\forall x\in A$
2. 利用已知集合等式或包含式，通过集合演算证明

命题逻辑

基本概念

• 命题：判断结果唯一的陈述句

• 联结词

  • 合取式：$A\land B$

  • 析取式：$A\lor B$

  • 否定式：$\neg A$

  • 蕴含式：$A\rightarrow B$ （1 0 0）

    ​ 当$p$为假时，$p\rightarrow q$为真

    ​ 除非$q$，否则$\neg p$

  • 等价式：$A\leftrightarrow B$ （同时为真或同时为假，同或）

  • 与非式：$A\uparrow B$

  • 或非式：$A\downarrow B$

• 赋值：给公式 A 中命题变项$p_1,p_2,\ldots,p_n$指定的一组真值$\alpha =\alpha_1,\alpha_2,\ldots,\alpha_n$，按使公式为真/假分为真/假赋值。

• 命题公式分类

  • 永真式：也叫重言式，在各种赋值下取值均为真（一定是可满足式）
  • 永假式：也叫矛盾式，在各种赋值下取值均为假
  • 可满足式：若 A 不是矛盾式，则其为可满足式（等价定义：A 至少存在一个成真赋值）

等值演算

概念

等值式：若 A 和 B 构成的等价式$A\leftrightarrow B$为重言式，则称 A 和 B 是等值的，记作$A\Leftrightarrow B$

等值演算：根据已知的等值式推演出与原命题公式等值的新的命题公式的过程

n 个命题变量的可能真值表共有$2^{2^n}$个

哑元：在 B 中出现，但不在 A 中出现的命题变项称作 A 的哑元。哑元的出现不影响命题公式的真值。

真值表法

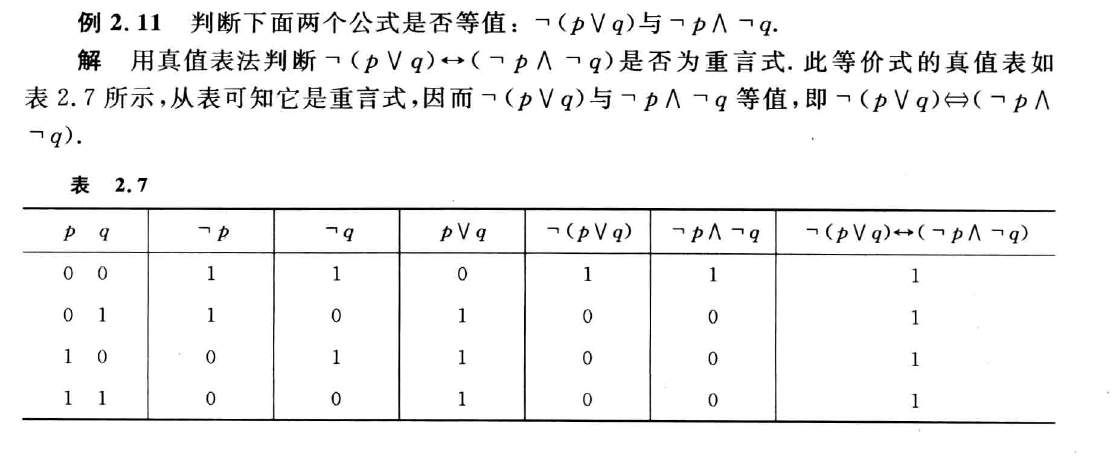
等值演算法

基本等值式

着重考虑置换规则：若$A\Leftrightarrow B$，则$\Phi(B)\Leftrightarrow \Phi(A)$

联结词完备集

真值函数

称$F:{0,1}^n\rightarrow {0,1}$为$n$元真值函数

特征

• $n$元真值函数共有$2^{2^n}$个
• 每个命题公式对应一个真值函数
• 每个真值函数对应无穷个命题公式

联结词完备集

设$S$是一个联结词集合，如果任何$n(n\ge 1)$元真值函数都可以由仅含$S$中的联结词构成的公式表示，则称$S$是联结词完备集

定理

• $S={\neg,\land,\lor}$是联结词完备集
  • 推论：$S={\neg,\land},\quad S={\neg,\lor}\quad S={\neg,\rightarrow}$
• ${\uparrow}\quad{\downarrow}$都是联结词完备集

范式

析取范式与合取范式

• 定义：

  • 命题变量及其否定统称作文字，仅由有限个文字构成的析/合取式称作简单析/合取式
  • 由有限个简单合取式构成的析取式称为析取范式（与或）
  • 由有限个简单析取式构成的合取式称为合取范式（或与）

• 定理

  • 一个简单析取式是重言式$\Leftrightarrow$他同时包含某个命题变量和他的否定
  • 一个简单合取式是矛盾式$\Leftrightarrow$他同时包含某个命题变量和他的否定
  • 一个析取范式是矛盾式$\Leftrightarrow$他每个简单合取式都是矛盾式
  • 一个析取合式是重言式$\Leftrightarrow$他每个简单析取式都是重言式
  • （范式存在定理）任意命题公式都存在着与之等值的析取范式和合取范式

• 求范式

  1. 消去联结词$\rightarrow,\leftrightarrow$
  2. 否定号的消去（双重否定律）或内移（德摩根定律）
  3. 利用分配律

• 例

  

主析取范式与主合取范式

• 极小项与极大项

$$ \neg m_i\Leftrightarrow M_i \ ,\quad \neg M_i\Leftrightarrow m_i $$

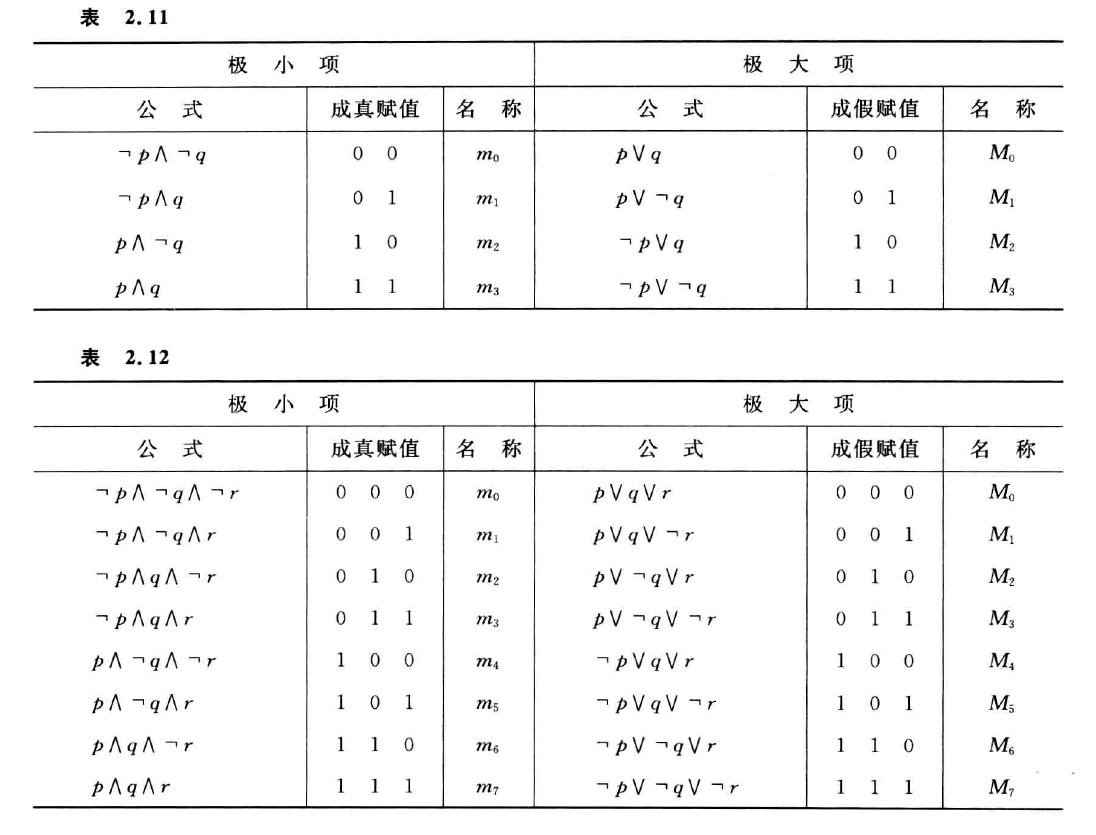
• 定义：若由 n 个命题变项构成的析\合取范式中所有的简单合\析取式都是极小\大项，则称其为主析\合取范式
• 定理：任意命题公式都存在着与之等值的主析取范式和主合取范式
• 求主范式步骤
  1. 求析\合取范式
  2. 展开（乘一\加零）
• 用途
  • 求取成真赋值和成假赋值
  • 判断公式类型

推理

推理的形式结构

称 $$ (A_1\land A_2\land \ldots\land A_k)\rightarrow B $$ 为由前提$A_1,A_2\ldots A_k$推结论$B$的推理的形式结构

当推理正确（重言式）时，记为 $$ (A_1\land A_2\land \ldots\land A_k)\Rightarrow B $$

• 判断推理正确的方式
  • 真值表法
  • 等值演算法
  • 主析取范式法
  • 观察法（?）

推理的证明

永真的蕴含式称为推理定律

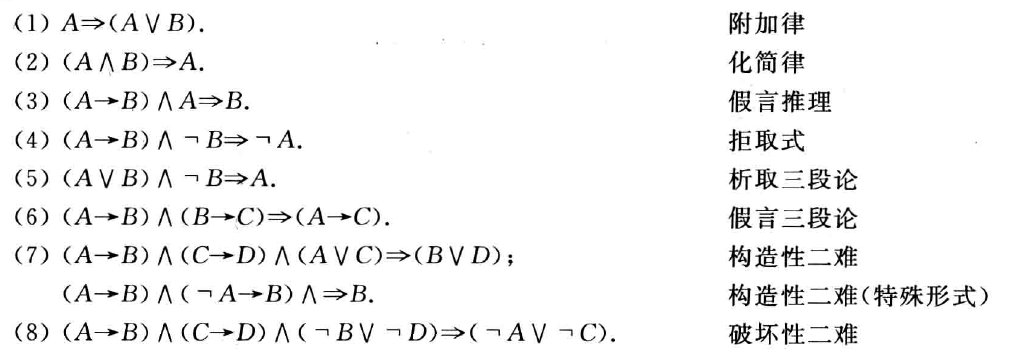
把一个公式换成任何与它等值的公式，称作等值置换，简称置换

证明方法

附加前提证明法

定义：当推理的结论为蕴含式$A\rightarrow B$时，把$A$加入推理的前提，把$B$作为推理的结论。$A$即为附加前提。

​ 即，把证明推理 $$ (A_1\land A_2\land \ldots\land A_k)\rightarrow (C\rightarrow B) $$ ​ 转换成证明推理 $$ (A_1\land A_2\land \ldots\land A_k\land C)\rightarrow B $$

归谬法

定义：把结论的否定加入前提，而要推出矛盾（以 0 为结论）。

​ 即，把证明推理 $$ (A_1\land A_2\land \ldots\land A_k)\rightarrow B $$ ​ 转换成证明推理 $$ (A_1\land A_2\land \ldots\land A_k\land \neg B)\rightarrow 0 $$

归结证明法

• 归结规则

  显然有

$$ (L\lor C_1)\land(\neg L \lor C_2)\Rightarrow C_1\lor C_2 $$

​ $L$是一个变元，$C_1$和$C_2$是简单析取式。称上式为归结定律 $$ \ \ L\lor C_1 \ \underline{\neg L\lor C_2}\ \ C_1\lor C_2 \ $$

• 基本思想：采用归谬法，把结论的否定引入前提。若推出空简单析取式（推出 0），则证明推理正确。
• 步骤
  • 把结论的否定引入前提
  • 把所有前提化成合取范式，将其中的所有简单析取式作为前提
  • 应用归结规则进行推理
  • 若推出空简单析取式（推出 0），则证明推理正确

一阶逻辑

一阶逻辑也叫一阶谓词逻辑或谓词逻辑

在一阶逻辑中，公式的可满足性、永真性、永假性是不可能判定的。

基本概念

个体词，谓词与量词

个体词

可以独立存在的具体或抽象的客体，分个体常项和个体变项

• 个体域：个体变项的取值范围
• 全总个体域：宇宙一切事物

谓词

刻画个体值性质及个体词间的关系，分谓词常项和谓词变项

• n 元谓词：$P(x_1,x_2,\ldots,x_n)$，值为 0 或 1
• 0 元谓词：不带个体变项的谓词
• 特性谓词：将个体词与其他事物区别开来的谓词，$M(x)$

量词

表示个体间的数量关系

• 全称量词：$\forall$

• 存在量词：$\exists$

符号化

一般而言，全称量词用蕴含，存在量词用合取。

一阶逻辑公式与分类

• 一阶语言字母表$\mathscr{L}$
  • 个体常项：$a,b,c,\ldots,a_i,b_i,c_i,\ldots,i\ge1$
  • 个体变项：$x,y,z,\ldots,x_i,y_i,z_i,\ldots,i\ge1$
  • 函数符号：$f,g,h,\ldots,f_i,g_i,h_i,\ldots,i\ge1$
  • 谓词符号：$F,G,H,\ldots,F_i,G_i,H_i,\ldots,i\ge1$
  • 量词符号：$\forall,\exists$
  • 联结词符号：$\neg,\land,\lor,\rightarrow,\leftrightarrow$
  • 括号与逗号：$(),,$
• 公式
  • 称$R(x_1,x_2,\ldots,x_n)$为原子公式（谓词+项）
  • 单一的原子公式或原子公式的各种组合称为合式公式（谓词公式），简称公式
• 辖域
  • 在公式 $\forall xA$ 和 $\exists xA$ 中，称 $x$ 为指导变元，$A$ 为相应量词的辖域
  • 在 $\forall x$ 和 $\exists x$ 的辖域中，$x$ 的所有出现都成为约束出现，$A$ 中不是约束出现的其他变项均称为是自由出现的
  • 若公式 $A$ 中不含自由出现的个体变项，则称 $A$ 为封闭的公式，简称闭式

• 解释与赋值

  
  • 闭式在任何解释下都变成命题
  • 公式在给定解释和赋值后即成为命题

• 代换实例：用一阶逻辑替代命题逻辑所得的公式

一阶逻辑的等值演算

四个等值式

$\forall$ 与 $\lor$、$\exists$ 与 $\and$ 无分配律

例题

置换、换名规则

一阶逻辑的等值演算同样满足置换规则和换名规则（换名只能换约束变量）

前束范式

定义：前面只能是量词的公式

定理：一阶逻辑任何公式都能化为前束范式