概率论 第八章
假设检验
引例



基本概念
理论性理解
假设
对未知总体分布的一个推断
关于总体分布类型的推断,叫非参数假设
关于总体分布参数的推断,叫参数假设
假设检验
- 检验假设正确与否
- 分参数假设检验与非参数假设检验
- 本章只关注参数假设检验
结合例子理解
在上例中,其中的 $H_0$ 称为原假设(零假设)
称$H_1$为备择假设,指原假设被拒绝后可供选择的假设
称给定的数 $\alpha$ 为显著水平
称 $Z=\cfrac{\overline X-\mu_0}{\sigma/\sqrt{n}}$ 为检验统计量
当检验统计量取某个区域$C$中的值时,就要拒绝原假设$H_0$,称区域$C$为拒绝域
称拒绝域的边界点为临界点
由于决策是依据一次抽样作出的,在原假设$H_0$为真时,可能犯拒绝$H_0$的错误,称这种“弃真”错误为第一类错误
其概率为$P{拒绝 H_0|H_0 为真}$,记为$P_{H_0}{H_1}$
同时在原假设$H_0$不真时,可能犯接受$H_0$错误,称这种“取伪”的错误为第二类错误
其概率为$P{接受 H_0|H_1 为真}$,记为$P_{H_1}{H_0}$
在样本容量一定时,若要使犯一类错误的概率减少,犯另一类错误的概率就会增加
显著性假设检验
控制犯第一类错误的概率的检验方法叫做显著性假设检验
步骤
- 提出一个原假设$H_0$,和与此相对的备择假设$H_1$
- 根据所做的假设,确定拒绝形式
- 确定检验统计量,并由$P_{H_0}{H_1}\le \alpha$确定拒绝域
- 通过抽样结果,作出拒绝域或接受$H_0$的决策(若检验统计量的观察值在拒绝域内,则拒绝$H_0$)
实际上,假设检验是一种带有概率意义的反证法
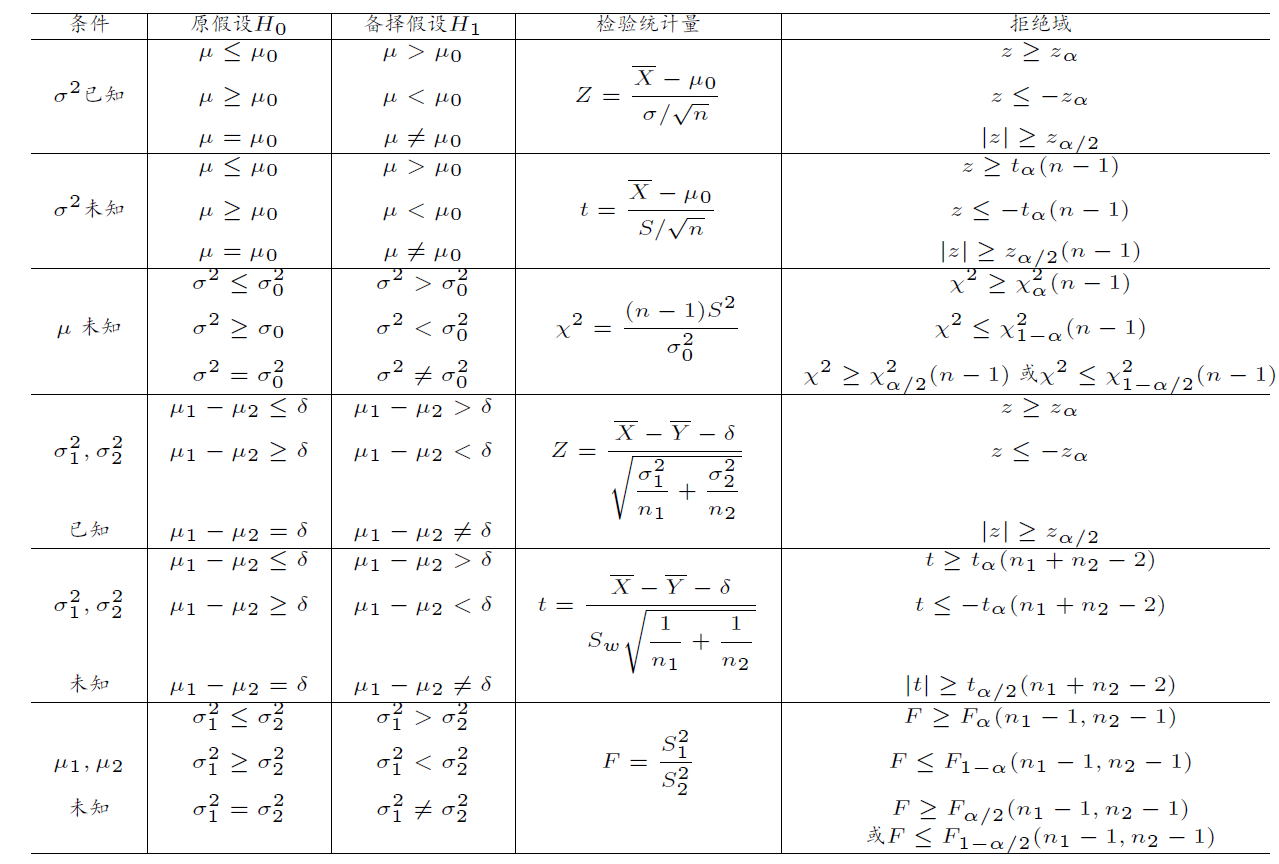
单个正态总体的假设检验
总体均值的假设检验
在总体方差$\sigma^2$已知的条件下
以$U=\cfrac{\overline X-\mu_0}{\sigma/\sqrt{n}}$为检验统计量,采用$z$检验法
- 双边检验:检验假设为$H_0:\mu=\mu_0,H_1:\mu\neq\mu_0$
$$ 拒绝域:|z|\ge z_{\alpha/2} $$
- 左边检验:检验假设为$H_0:\mu\ge\mu_0,H_1:\mu<\mu_0$
$$ 拒绝域:z\le -z_\alpha $$
- 右边检验:检验假设为$H_0:\mu\le\mu_0,H_1:\mu>\mu_0$
$$ 拒绝域:z\ge z_\alpha $$
在总体方差$\sigma^2$未知的条件下
以$T=\cfrac{\overline X-\mu_0}{S/\sqrt{n}}$为检验统计量,采用$t$检验法
- 双边检验:检验假设为$H_0:\mu=\mu_0,H_1:\mu\neq\mu_0$
$$ 拒绝域:|t|\ge t_{\alpha/2}(n-1) $$
- 左边检验:检验假设为$H_0:\mu\ge\mu_0,H_1:\mu<\mu_0$
$$ 拒绝域:t\le-t_{\alpha}(n-1) $$
- 右边检验:检验假设为$H_0:\mu\le\mu_0,H_1:\mu>\mu_0$
$$ 拒绝域:t\ge t_{\alpha}(n-1) $$
总体方差的假设检验
在$\mu$未知的条件下,以$\chi^2=\cfrac{(n-1)S^2}{\sigma_0^2}$为检验统计量,采用$\chi^2$检验法
- 双边检验:检验假设为$H_0:\sigma^2=\sigma_0^2,H_1:\sigma^2\neq\sigma_0^2$,拒绝域为
$$ \chi^2\le\chi_{1-\alpha/2}^2(n-1) \ 或 \ \chi^2\ge\chi_{\alpha/2}^2(n-1) $$
- 左边检验:检验假设为$H_0:\sigma^2\ge\sigma_0^2,H_1:\sigma^2<\sigma_0^2$,拒绝域为
$$ \chi^2\le\chi_{1-\alpha}^2(n-1) $$
- 右边检验:检验假设为$H_0:\sigma^2\le\sigma_0^2,H_1:\sigma^2>\sigma_0^2$,拒绝域为
$$ \chi^2\le\chi_{\alpha}^2(n-1) $$



双正态总体的假设检验
总体均值差的检验
在总体方差$\sigma_1^2,\sigma_2^2$已知的条件下
以$Z=\cfrac{\overline{X_1}-\overline{X_2}-\delta}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}$为检验统计量,采用$z$检验法
- 双边检验:检验假设为$H_0:\mu_1-\mu_2=\delta,H_1:\mu_1-\mu_2\neq\delta$,拒绝域为
$$ |z|\ge z_{\alpha/2} $$
- 左边检验:检验假设为$H_0:\mu_1-\mu_2\ge\delta,H_1:\mu_1-\mu_2<\delta$,拒绝域为
$$ z\le-z_\alpha $$
- 右边检验:检验假设为$H_0:\mu_1-\mu_2\le\delta,H_1:\mu_1-\mu_2\delta$,拒绝域为
$$ z\ge z_\alpha $$
在总体方差$\sigma_1^2,\sigma_2^2$未知的条件下
以$T=\cfrac{\overline{X_1}-\overline{X_2}-\delta}{S_w\sqrt{1/n_1+1/n_2}}$为检验统计量,采用$t$检验法
- 双边检验:检验假设为$H_0:\mu_1-\mu_2=\delta,H_1:\mu_1-\mu_2\neq\delta$,拒绝域为
$$ |t|\ge t_{\alpha/2}(n_1+n_2-2) $$
- 左边检验:检验假设为$H_0:\mu_1-\mu_2\ge\delta,H_1:\mu_1-\mu_2<\delta$,拒绝域为
$$ t\le-t_\alpha(n_1+n_2-2) $$
- 右边检验:检验假设为$H_0:\mu_1-\mu_2\le\delta,H_1:\mu_1-\mu_2>\delta$,拒绝域为
$$ t\ge t_\alpha(n_1+n_2-2) $$
总体方差相等的假设检验
在$\mu_1,\mu_2$未知的条件下,以$F=\cfrac{S_1^2}{S_2^2}$为检验统计量,采用$F$检验法
- 双边检验:检验假设为$H_0:\sigma_1^2=\sigma_2^2,H_1:\sigma_1^2\neq\sigma_2^2$,拒绝域为
$$ F\le F_{1-\alpha/2}(n_1-1,n_2-1) \ 或 \ F\ge F_{\alpha/2}(n_1-1,n_2-1) $$
- 左边检验:检验假设为$H_0:\sigma^2\ge\sigma_0^2,H_1:\sigma^2<\sigma_0^2$,拒绝域为
$$ F\le F_{1-\alpha}(n_1-1,n_2-1) $$
- 右边检验:检验假设为$H_0:\sigma^2\le\sigma_0^2,H_1:\sigma^2>\sigma_0^2$,拒绝域为
$$ F\ge F_{\alpha}(n_1-1,n_2-1) $$