参数估计

统计推断的基本问题分为两类：一是估计问题，另一个是假设检验。本章主要讨论总体参数的点估计和区间估计。

点估计

用总体 $\Bbb X$ 的一个样本来估计总体未知参数的方法称为点估计法

术语

设 $X_1,X_2,\ldots,X_n$ 是来自总体 $\Bbb X$ 的一个样本，点估计法就是要构建一个合适的统计量$\hat{\theta}(X_1,X_2,\ldots,X_n)$用它的观察值$\hat{\theta}(x_1,x_2,\ldots,x_n)$作为未知参数$\theta$的近似值，有

• 估计量：$\hat{\theta}(X_1,X_2,\ldots,X_n)$

• 估计值：$\hat{\theta}(x_1,x_2,\ldots,x_n)$

估计量和估计值统称为估计

矩估计法

用样本矩作为相应的总体矩的估计方法称为矩估计法

方法

设$\theta_1,\theta_2,\ldots,\theta_k$为带估计的参数，用$\Theta$表示带估计参数组成的向量，即$\Theta=(\theta_1,\theta_2,\ldots,\theta_k)$

• $\Bbb X$ 为连续型总体，其概率密度为 $f(x,\Theta)$，总体的前 $k$ 阶矩为

$$ \mu_l(\Theta)=E(X^l)=\int_{-\infty}^{+\infty}x^lf(x,\Theta)dx\quad l=1,2,\ldots,k $$

• $\Bbb X$ 为离散型总体，其分布律为 $P{X=x_i}=p_i(\Theta),i=1,2,\ldots,k$，总体的前 $k$ 阶矩为

$$ \mu_l(\Theta)=E(X^l)=\sum\limits_{i=1}^{\infty}(x_i)^lp_i(\Theta)\quad l=1,2,\ldots,k $$

设$X_1,X_2,\ldots,X_n$为来自总体$\Bbb X$的一个样本，它的前$k$阶样本矩观察值为 $$ a_l=\cfrac{1}{n}\sum\limits_{i=1}^nx_i^l\quad (l=1,2,\ldots,k) $$

然后列方程（组） $$ \begin{cases} \ \mu_1(\theta_1,\theta_2,\ldots,\theta_k)=a_1 \ \ \mu_2(\theta_1,\theta_2,\ldots,\theta_k)=a_2 \ \ \vdots \ \ \mu_k(\theta_1,\theta_2,\ldots,\theta_k)=a_k \end{cases} $$

最后求解方程（组），即可获得未知参数$\theta_1,\theta_2,\ldots,\theta_k$的估计值为 $$ \hat{\theta}_l=\theta_l(a_1,a_2,\ldots,a_k)\quad (l=1,2,\ldots,k) $$ 因此估计量为 $$ \hat{\theta}_l=\theta_l(A_1,A_2,\ldots,A_k)\quad (l=1,2,\ldots,k) $$

例

结论

1. 总体期望可以由样本均值（一阶中心矩）表示，$\overline{X} 或 A_1$
2. 总体方差可以由样本二阶中心矩表示，$A_2$

最大似然估计法

设 $\theta_1,\theta_2,\ldots,\theta_k$ 为带估计的参数，用$\Theta$表示带估计参数组成的向量，即$\Theta=(\theta_1,\theta_2,\ldots,\theta_k)$

设$x_1,x_2,\ldots,x_n$是一组抽样值，这意味着${X_1=x_1,X_2=x_2,\ldots,X_n=x_n}$是一个大概率事件。

最大似然估计法就是要确定未知参数的值，使得$P{X_1=x_1,X_2=x_2,\ldots,X_n=x_n}$（这其中含有未知参数）为最大。

方法

• $\Bbb X$ 为离散型总体，其分布律为 $P{X=x_i}=p_i(\Theta),i=1,2,\ldots,k$，设$x_1,x_2,\ldots,x_n$是一组抽样值

$$ P{X_1=x_1,X_2=x_2,\ldots,X_n=x_n}=\prod\limits_{i=1}^np_i(\Theta),令\ L(x_1,x_2,\ldots,x_n;\Theta)=\prod\limits_{i=1}^np_i(\Theta) $$

• $\Bbb X$ 为连续型总体，其概率密度为 $f(x,\Theta)$，设$x_1,x_2,\ldots,x_n$是一组抽样值

$$ P{X_1=x_1,X_2=x_2,\ldots,X_n=x_n}\approx\prod\limits_{i=1}^nf(x_i;\Theta) $$

​ 其中$\prod\limits_{i=1}^ndx_i$与未知参数$\Theta$无关 $$ L(x_1,x_2,\ldots,x_n;\Theta)=\prod\limits_{i=1}^nf(x_i;\Theta) $$ 称 $$ L=(x_1,x_2,\ldots,x_n;\theta_1,\theta_2,\ldots,\theta_k) $$

为似然函数，其自变量为$\theta_1,\theta_2,\ldots,\theta_k$。

最大似然估计就是要确定参数取何值时似然函数达到最大值。

通常利用对数似然函数来求，即求 $$ \cfrac{\partial}{\partial\theta_i}lnL(x_1,x_2,\ldots,x_n;\theta_1,\theta_2,\ldots,\theta_k)=0\qquad(i=1,2,\ldots,k) $$ 来求得未知参数的估计值$\hat\theta_1,\hat\theta_2,\ldots,\hat\theta_k$，再将其估计值改为估计量

例

步骤

1. 求总体的分布律/概率密度
2. 写出似然函数

$$ L(\Theta)=\prod\limits_{i=1}^np_i(\Theta)\ 或 \ L(\Theta)=\prod\limits_{i=1}^nf(x_i;\Theta) $$

3. 取对数，求导

$$ \cfrac{\partial}{\partial\Theta}lnL=… $$

估计量的评选标准

无偏性

若估计量 $\hat\theta=\hat\theta(X_1,X_2,\ldots,X_n)$ 的数学期望 $E(\hat\theta)$ 存在，且对任意 $\theta\in \Theta$ 有 $$ E(\hat\theta)=\theta $$ 则称$\hat\theta$是$\theta$的无偏估计量

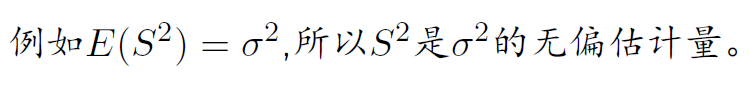
有效性

设$\hat\theta_1=\hat\theta_1(X_1,X_2,\ldots,X_n)$与$\hat\theta_2=\hat\theta_2(X_1,X_2,\ldots,X_n)$都是$\theta$的无偏估计量，若对任意的$\theta\in \Theta$，有 $$ D(\hat\theta_1)\le D(\hat\theta_2) $$ 则称 $\hat\theta_1$ 较 $\hat\theta_2$ 有效

相合性

设 $\hat\theta=\hat\theta(X_1,X_2,\ldots,X_n)$ 是参数 $\theta$ 的估计量，若对于任意的 $\theta\in \Theta$，对于任意 $\varepsilon>0$ 有 $$ \lim\limits_{n\rightarrow\infty}P{|\hat\theta-\theta|<\varepsilon}=1 $$ 则称 $\hat\theta$ 是 $\theta$ 的相合估计量

区间估计

置信区间

设总体 $\Bbb X$ 的分布含有一个未知参数 $\theta$，对于给定的 $\alpha(0<\alpha<1)$，由来自 $\Bbb X$ 的样本 $X_1,X_2,\ldots,X_n$ 确定的两个统计量$\underline\theta=\underline\theta(X_1,X_2,\ldots,X_n)$ 和 $\overline\theta=\overline\theta(X_1,X_2,\ldots,X_n)$，对任意 $\theta\in\Theta$ 都有 $$ P{\underline\theta<\theta<\overline\theta}\ge 1-\alpha $$ 则称随机区间 $(\underline\theta,\overline\theta)$为 $\theta$ 的一个置信水平为 $1-\alpha$ 的置信区间，

• $\underline\theta$：双侧置信下限

• $\overline\theta$：双侧置信上限

• $1-\alpha$：置信水平

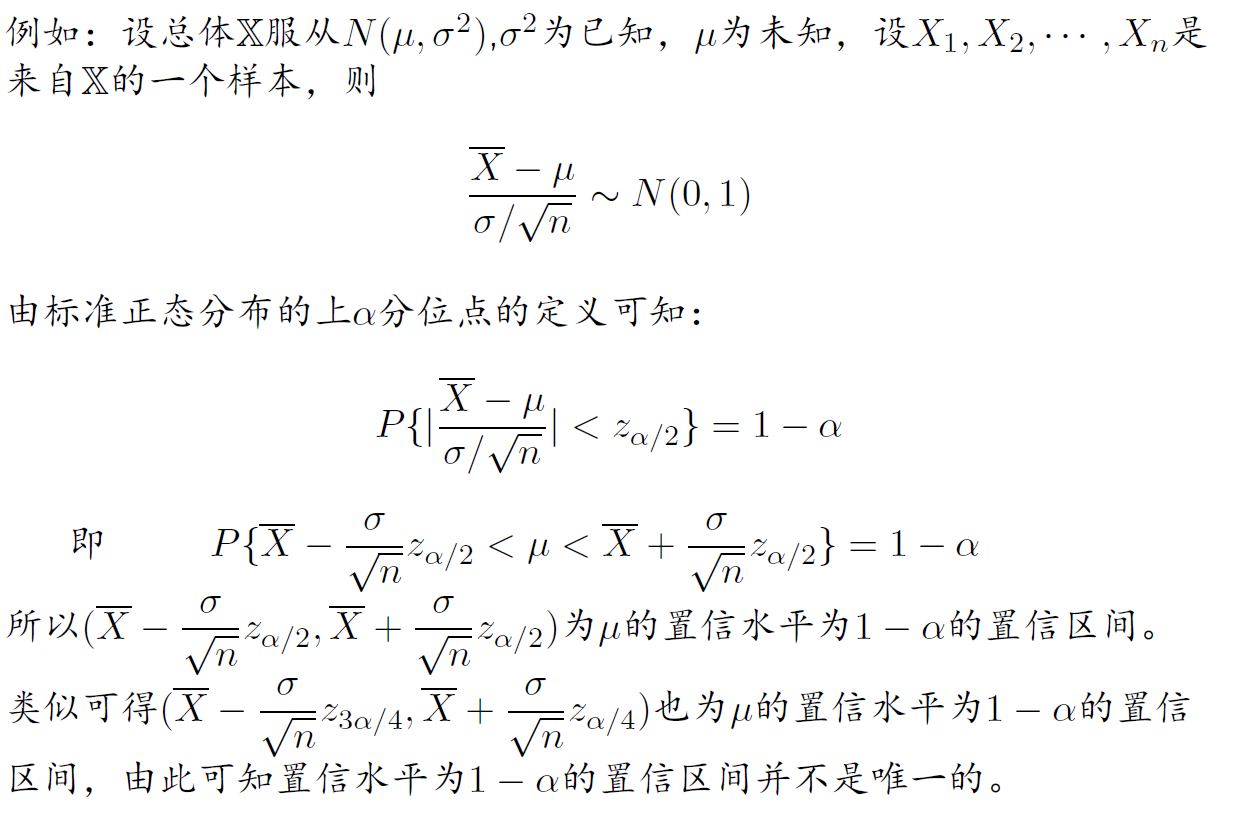
区间估计

求出一个合适的置信水平为 $1-\alpha$ 的置信区间，使得该区间包含参数 $\theta$ 真值的可信程度为置信水平 $1-\alpha$

步骤

1. 寻求一个样本 $X_1,X_2,\ldots,X_n$ 和 $\theta$ 的函数 $W=W(X_1,X_2,\ldots,X_n,\theta)$，使其分布是已知（但该分布与$\theta$无关），（通常称这个$W$为枢轴量）
2. 对给定的置信水平 $1-\alpha$，由双侧分位点确定 $a$ 和 $b$，使得

$$ P{a<W(X_1,X_2,\ldots,X_n,\theta)<b}=1-\alpha $$

3. 由 $a<W(X_1,X_2,\ldots,X_n,\theta)$ 得出 $\underline\theta<\theta<\overline\theta$，则 $(\underline\theta,\overline\theta)$ 为所求的 $\theta$ 的置信水平为 $1-\alpha$ 的置信区间

正态总体均值与方差的区间估计

单个总体的情况

1. 方差$\sigma^2$已知的条件下均值$\mu$的置信区间（略）
2. 方差$\sigma^2$未知的条件下均值$\mu$的置信区间

$$ (\overline X\pm\cfrac{S}{\sqrt{n}}t_{\alpha/2}(n-1)) $$

3. 方差$\sigma^2$的置信区间

$$ (\cfrac{(n-1)S^2}{\chi^2_{\alpha/2}(n-1)},\cfrac{(n-1)S^2}{\chi^2_{1-\alpha/2}(n-1)}) $$

两个总体的情况

1. $\sigma_1^2,\sigma_2^2$已知，$\mu_1-\mu_2$的区间估计，枢轴量为

$$ Z=\cfrac{\overline X-\overline Y-(\mu_1-\mu_2)}{\sqrt{\cfrac{\sigma_1^2}{n_1}+\cfrac{\sigma_2^2}{n_2}}}\sim N(0,1) $$

2. $\sigma_1^2,\sigma_2^2$未知，$\mu_1-\mu_2$的区间估计，枢轴量为

$$ t=\cfrac{\overline X-\overline Y-(\mu_1-\mu_2)}{S_w\sqrt{\cfrac{1}{n_1}+\cfrac{1}{n_2}}}\sim t(n_1+n_2-2) $$

3. $\mu_1,\mu_2$未知，$\cfrac{\sigma_1^2}{\sigma_2^2}$的区间估计，枢轴量为

$$ F=\cfrac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2}\sim F(n_1-1,n_2-1) $$

总结

例

单侧置信区间