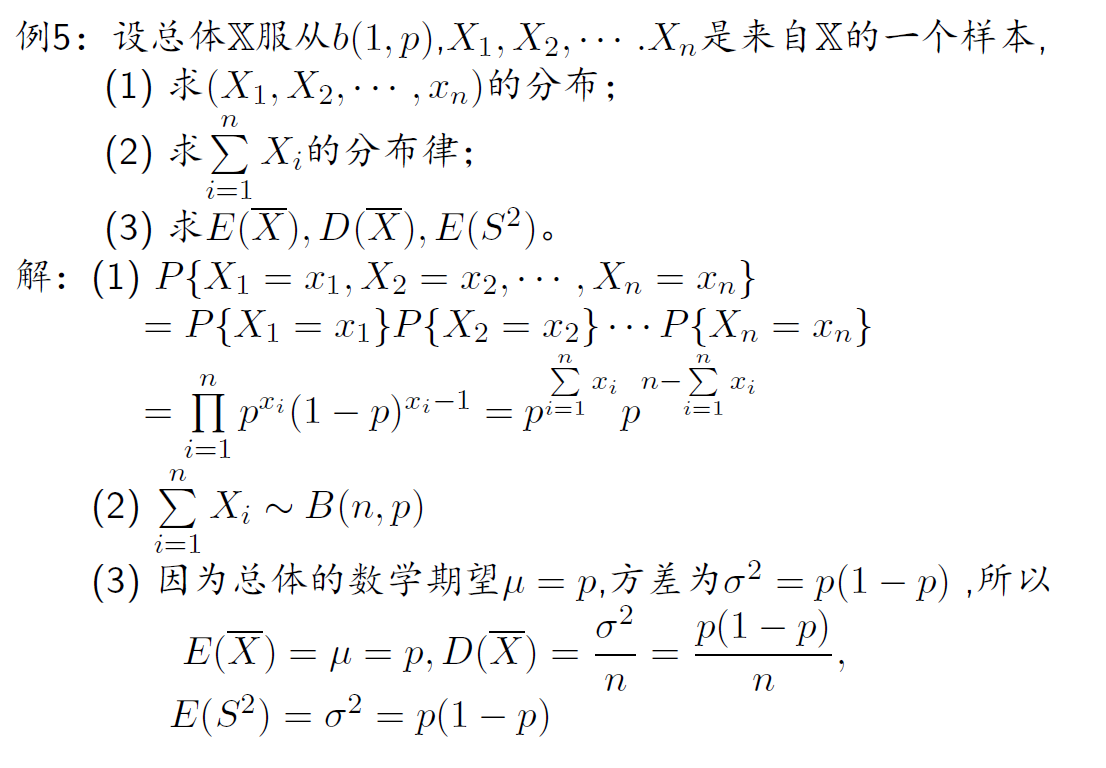概率论 第六章
样本及抽样分布
数理统计的基本概念
总体与个体
- 总体(母体):具有一定共性的研究对象的全体,记为 $\Bbb{X}$
- 个体:构成总体的每一个成员
- 总体的容量:个体的个数
样本与样本分布
- 抽样:按一定的原则从$\Bbb{X}$中抽取若干个体
- 样本:被抽出的部分个体(相互独立且同分布),记作$X_1,X_2,\ldots,X_n$
- 总体分布:每一个个体可以看作一个随机变量,这个随机变量的分布即为总体分布
- 样本容量:样本是一组随机变量$X_1,X_2,\ldots,X_n$,$n$即为样本容量
- 样本值:对样本进行一次观察得到的一组观察值$x_1,x_2,\ldots,x_n$
- 样本分布:样本$(X_1,X_2,\ldots,X_n)$的概率分布,有
$$ F(x_1,x_2,\ldots,x_n)=F(x_1)F(x_2)\ldots F(x_n)\ f(x)=f(x_1)f(x_2)\ldots f(x_n) $$
统计量
定义
设 $X_1,X_2,\ldots,X_n$ 是来自总体 $\Bbb{X}$ 的一个样本,称此样本的任一不含总体分布未知参数的函数为该样本的统计量
统计量是随机变量,不是一个数
常见的统计量及其观察值分布
- 样本均值
$$ \overline{X}=\cfrac{1}{n}\sum\limits_{i=1}^{n}X_i\ \overline{x}=\cfrac{1}{n}\sum\limits_{i=1}^{n}x_i $$
- 样本方差
$$ S^2=\cfrac{1}{n-1}\sum\limits_{i=1}^{n}(X_i-\overline{X})^2=\cfrac{1}{n-1}(\sum\limits_{i=1}^{n}X_i^2-n\overline{X}^2)\ s^2=\frac{1}{n-1}\sum\limits_{i-1}^n(x_i-\overline{x})^2 $$
- 样本标准差
$$ S=\sqrt{\cfrac{1}{n-1}\sum\limits_{i=1}^{n}(X_i-\overline{X})^2}\ s=\sqrt{\frac{1}{n-1}\sum\limits_{i-1}^n(x_i-\overline{x})^2} $$
- 样本 k 阶(原点)矩
$$ A_k=\cfrac{1}{n}\sum\limits_{i=1}^nX_i^k\qquad k=1,2,\ldots\ a_k=\cfrac{1}{n}\sum\limits_{i=1}^nx_i^k $$
- 样本 k 阶中心矩
$$ B_k=\cfrac{1}{n}\sum\limits_{i=1}^n(X_i-\overline{X})^k\qquad k=2,3,\ldots\ b_k=\cfrac{1}{n}\sum\limits_{i=1}^n(x_i-\overline{x})^k $$
抽样分布
概念
称统计量的分布为抽样分布(统计分布)
分类
$\chi ^2$ 分布
- 定义
设 $X_1,X_2,\ldots,X_n$ 是来自总体 $N(0,1)$ 的样本,则称统计量 $$ \chi^2=X_1^2+X_2^2+\ldots+X_n^2=\sum\limits_{i=1}^{n}X_i^2 $$ 服从自由度为 $n$ 的 $\chi^2$ 分布,记作 $\chi^2\sim \chi^2(n)$
- 性质
- $\chi_1^2+\chi_2^2\sim \chi^2(n_1+n_2)$
- $E(\chi^2)=n\qquad D(\chi^2)=2n$
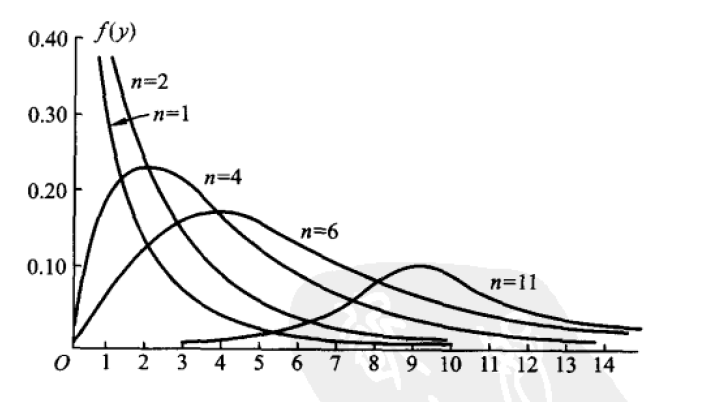
- 图形特征(扩展)
- 单峰曲线,在 n-2 时取到最大值
- 不对称,n 越大越对称
- 当 n 很大时可用正态分布来近似
$t$ 分布
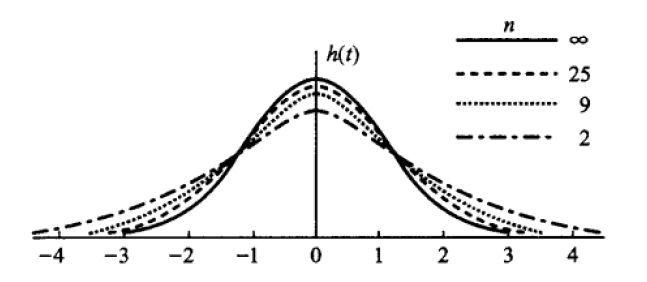
设$X\sim N(0,1),Y\sim \chi^2(n)$,且 $X,Y$ 相互独立,则称统计量 $$ t=\cfrac{X}{\sqrt{Y/n}} $$ 服从自由度为 $n$ 的 $t$ 分布(学生氏分布),记作 $t\sim t(n)$
$F$ 分布
设 $U\sim \chi^2(n_1),V\sim \chi^2(n_2)$,且 $U,V$ 相互独立,则称统计量 $$ F=\cfrac{U/n_1}{V/n_2} $$ 服从自由度为 $(n_1,n_2)$的 $F$ 分布,记作 $F\sim F(n_1,n_2)$

分位数
(Quantile)
概念
对随机变量$X,0<\alpha<1$
- 若$P{X>t_\alpha}=\alpha$,则称$t_\alpha$为$X$的上$\alpha$分位点
- 若$P({X<t_{\alpha_1}}\cup{X>t_{\alpha_2}})=\alpha(\alpha_1+\alpha_2=1)$,则称$t_{\alpha_1}$和$t_{\alpha_2}$为$X$的双侧$\alpha$分位点
通常取$\alpha_2=\alpha/2,\alpha_1=1-\alpha/2$
常见分布的分位点
标准正态分布
设 $X\sim N(0,1)$,若数 $z_\alpha$ 满足 $$ P{X>z_\alpha}=\alpha,0<\alpha<1 $$ 则称 $z_\alpha$ 为标准正态分布的上 $\alpha$ 分位点

$\chi^2$ 分布
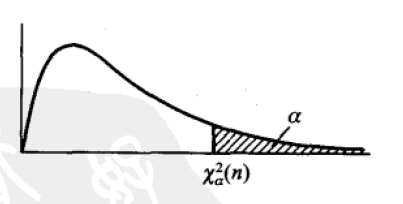
设$\mathcal{X}^2\sim X^2(n)$,若数${\mathcal X_\alpha^2}(n)$满足 $$ P{\mathcal{X}^2>X_\alpha^2(n)}=\alpha,0<\alpha<1 $$ 则称${\mathcal{X}_\alpha^2}(n)$为$\mathcal{X^2}(n)$分布的上$\alpha$分位点
$t$ 分布
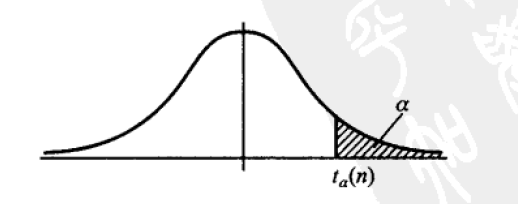
设 $t\sim t(n)$,若数 $t_\alpha(n)$ 满足 $$ P{t>t_\alpha(n)}=\alpha,0<\alpha<1 $$ 则称 $t_\alpha(n)$ 为 $t(n)$分布的上 $\alpha$ 分位点
- 有$t_{1-\alpha}(n)=-t_\alpha(n)$
$F$ 分布
设 $F\sim F(n_1,n_2)$,若数 $F_\alpha(n_1,n_2)$ 满足 $$ P{F>F_\alpha(n_1,n_2)}=\alpha,0<\alpha<1 $$ 则称 $F_\alpha(n_1,n_2)$ 为$F$分布的上 $\alpha$ 分位点
- 有$F_\alpha(n_1,n_2)=\cfrac{1}{F_{1-\alpha}(n_2,n_1)}$

总结
| 分布名 | 上 $\alpha$ 分位点 | 双侧 $\alpha$ 分位点 |
|---|---|---|
| 标准正态分布 | $z_\alpha$ | $\pm z_{\alpha/2}$ |
| $\mathcal X^2$ 分布 | ${\mathcal X_\alpha^2}(n)$ | ${\mathcal X}^2_{\alpha/2}(n)\{\mathcal X}^2_{1-\alpha/2}(n)$ |
| $t$ 分布 | $t_\alpha(n)$ | $\pm t_{\alpha/2}(n)$ |
| $F$ 分布 | $F_\alpha(n_1,n_2)$ | $F_{\alpha/2}(n_1,n_2)\F_{1-\alpha/2}(n_1,n_2)$ |
正态总体的样本均值与样本方差的分布
设总体$\Bbb X$的均值为$\mu$,方差为$\sigma^2$,$X_1,X_2,\ldots,X_n$是来自$\Bbb X$的一个样本,$\overline{X}$和$S^2$分别为该样本的样本均值和样本方差,则 $$ E(\overline{X})=\mu,D(\overline{X})=\cfrac{\sigma^2}{n}\ E(S^2)=\sigma^2 $$
定理一
设总体$\Bbb X$的分布为$N(\mu,\sigma^2)$,$X_1,X_2,\ldots,X_n$是来自$\Bbb X$的一个样本,$\overline{X}$为该样本的样本均值,则 $$ (1) \quad \overline{X}\sim N(\mu,\sigma^2/n)\qquad (2)\quad\cfrac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0,1) $$
定理二
设总体$\Bbb X$的分布为$N(\mu,\sigma^2)$,$X_1,X_2,\ldots,X_n$是来自$\Bbb X$的一个样本,$\overline{X}$和$S^2$分别为该样本的样本均值和样本方差,则
$$
(1)\quad\cfrac{n-1}{\sigma^2}S^2\sim\chi^2(n-1)\qquad(2)\quad\overline{X}与 S^2 相互独立
$$

定理三
设总体$\Bbb X$的分布为$N(\mu,\sigma^2)$,$X_1,X_2,\ldots,X_n$是来自$\Bbb X$的一个样本,$\overline{X}$和$S^2$分别为该样本的样本均值和样本方差,则 $$ \cfrac{\overline{X}-\mu}{S/\sqrt{n}}\sim t(n-1) $$
定理四
设 $X_1,X_2,\ldots,X_{n1}$ 与 $Y_1,Y_2,\ldots,Y_{n2}$ 分别是来自两个相互独立的正态总体 $N(\mu_1,\sigma^2_1)$ 和 $N(\mu_2,\sigma^2_2)$ 的样本,$\overline{X}$ 和$ \overline{Y}$ 分别为这两个样本的样本均值,$S_1^2$ 和 $S_2^2$ 分别为这两个样本的样本方差,则 $$ (1)\quad\cfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/n_1+\sigma_2^2/n_2}}\sim N(0,1)\qquad(2)\quad\cfrac{S_1^2/S_2^2}{\sigma_1^2/\sigma_2^2}\sim F(n_1-1,n_2-1)
\(3)当\sigma^2_1=\sigma^2_2=\sigma^2 时,\quad\cfrac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_w\sqrt{\cfrac{1}{n_1}+\cfrac{1}{n_2}}}\sim t(n_1+n_2-2) \其中 S_w=\sqrt{\cfrac{(n_1-1)S_1^2+(n_2-1)S^2_2}{n_1+n_2-2}} $$ 例