概率论 第四章
随机变量的数字特征
定义:这些用来描述随机变量统 计特征的数字,称为随机变量的数字特征。
最常用的数字特征有:数学 期望(均值)、方差、相关系数和矩。
数学期望 E(x)
(Expectation)
定义
设离散型随机变量$X$的分布律为$P{X=x_k}=p_k,\quad (k=1,2,\ldots)$,若级数$\sum\limits_{k=1}^\infty x_kp_k$绝对收敛,则称级数$\sum\limits_{k=1}^\infty x_kp_k$的和为$X$的数学期望(均值),记为$E(X)$;
设连续型随机变量$X$的概率密度为$f(x)$,若积分$\int_{-\infty}^{+\infty}xf(x)dx$绝对收敛,则称级数$\int_{-\infty}^{+\infty}xf(x)dx$的和为$X$的数学期望(==均值==),记为$E(X)$;
例

性质
- $E(C)=C$
- $E(CX)=CE(X)$
- $E(X+Y)=E(X)+E(Y)$
- 若$X$与$Y$相互独立,则$E(XY)=E(X)E(Y)$
六个常见随机变量的数学期望
(0-1)分布
$$ E(X)=p $$
二项分布 $B(n,p)$
$$ E(X)=np $$
泊松分布 $\pi(\lambda)$
$$ E(X)=\lambda $$
均匀分布 $U(a,b)$
$$ E(X)=\cfrac{a+b}{2} $$
指数分布 $e(\lambda)$
$$ E(X)=\cfrac{1}{\lambda} $$
正态分布 $N(\mu,\sigma^2)$
$$ E(X)=\mu $$
随机变量的函数的数学期望
$X$为离散型的,$Y=g(X)$的均值
若$X$的分布律为$P{X=x_i}=p_i\quad (i=1,2,\ldots)$,则 $$ E(Y)=\sum\limits_{i=1}^\infty g(x_i)p_i $$
$(X,Y)$为离散型的,$Z=g(X,Y)$的均值
若$(X,Y)$的分布律为$P{X=x_i,Y=y_i}=p_{i,j}\quad (i,j=1,2,\ldots)$,则 $$ E(Z)=\sum\limits_{i,j}g(x_i,y_i)p_{i,j} $$
$X$为连续型的,$Y=g(X)$的均值
若$X$的概率密度为$f_X(x)$,则 $$ E(Y)=\int_{-\infty}^{+\infty}g(x)f_X(x)dx $$
$(X,Y)$为连续型的,$Z=g(X,Y)$的均值
若$(X,Y)$的概率密度为$f(x,y)$,则 $$ E(Z)=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)dxdy $$
例



方差 D(X)
(Variance)
定义
设$X$是一个对随机变量,若$E{[X-E(X)]^2}$存在,则称其为$X$的方差,记为$D(X)$或$Var(X)$
称$\sqrt{D(X)}$为标准差或均方差,记为$\sigma(X)$
认识
标准差、方差越大,离散程度越大,若$X$的取值比较集中,则方差$D(X)$较小,若$X$的取值比较分散,则方差$D(X)$较大。因此,$D(X)$是刻画$X$取值分散程度的一个量,它是衡量取值分散程度的一个尺度
==公式==
$$ D(X)=E(X^2)-[E(X)]^2 $$
性质
$D(C)=0$
$D(CX)=C^2D(X)$
$D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}$
若$X$,$Y$相互独立,则有$D(X+Y)=D(X)+D(Y)$,又有$D(X-Y)=D(X)+D(Y)$
常见随机变量的方差
(0-1)分布
$$ D(X)=p(1-p) $$
二项分布 $B(n,p)$
$$ D(X)=np(1-p) $$
泊松分布 $\pi(\lambda)$
$$ D(X)=\lambda $$
均匀分布 $U(a,b)$
$$ D(X)=\cfrac{(b-a)^2}{12} $$
指数分布 $e(\lambda)$
$$ D(X)=\cfrac{1}{\lambda^2} $$
正态分布 $N(\mu,\sigma^2)$
$$ D(X)=\sigma^2 $$
==随机变量参考总结==
| 分布名称 | 分布律或概率密度 | 数学期望 | 方差 |
|---|---|---|---|
| (0-1)分布 | $P{X=k}=p^k(1-p)^{1-k}$ | $p$ | $p(1-p)$ |
| 二项分布 $B(n,p)$ | $P{X=k}=C_n^kp^k(1-p)^{n-k}$ | $np$ | $np(1-p)$ |
| 泊松分布 $\pi(\lambda)$ | $P{X=k}=e^{-\lambda}\cfrac{\lambda^k}{k!}$ | $\lambda$ | $\lambda$ |
| 均匀分布 $U(a,b)$ | $f(x)=\begin{cases}\ \cfrac{1}{b-a}\qquad a<x<b\ \ 0\qquad\qquad 其他\end{cases}$ | $\cfrac{a+b}{2}$ | $\cfrac{(b-a)^2}{12}$ |
| 指数分布 $e(\lambda)$ | $f(x)=\begin{cases}\ \lambda e^{-\lambda x}\qquad x\ge 0\ \ 0\qquad\qquad 其他\end{cases}$ | $\cfrac{1}{\lambda}$ | $\cfrac{1}{\lambda^2}$ |
| 正态分布 $N(\mu,\sigma^2)$ | $f(x)=\cfrac{1}{\sqrt{2\pi}\sigma}e^{-\cfrac{(x-\mu)^2}{2\sigma^2}}$ | $\mu$ | $\sigma^2$ |
例
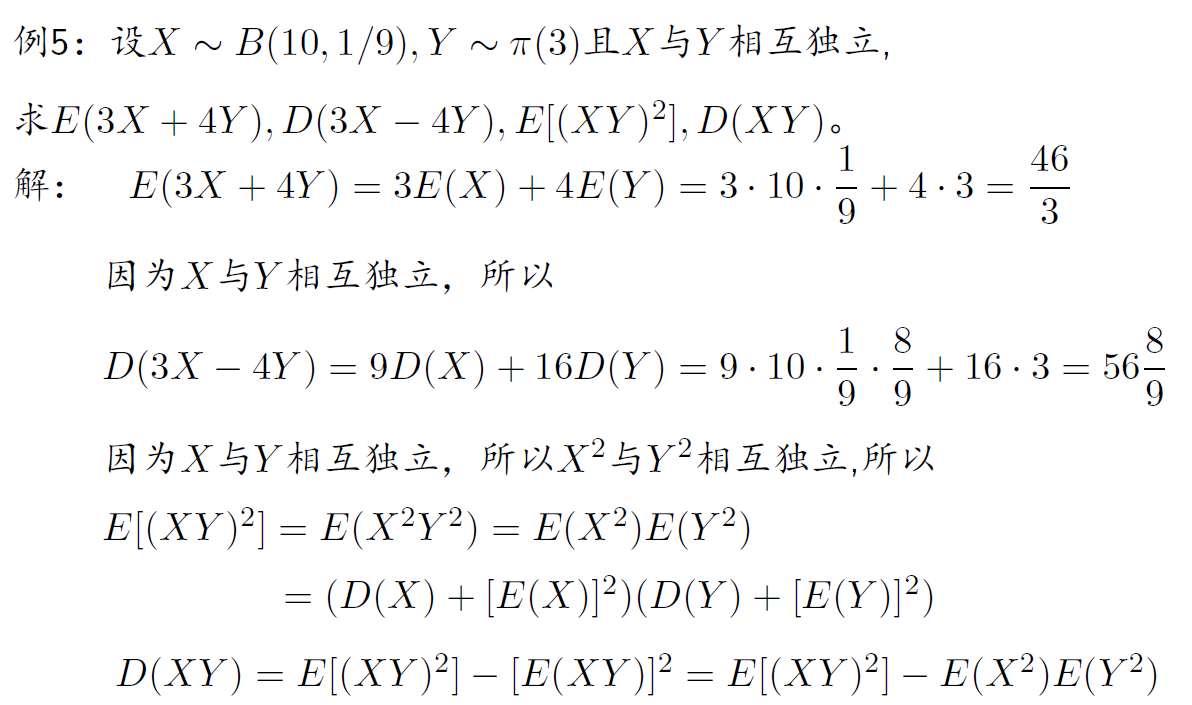
协方差
定义
设$(X,Y)$为二维随机变量,若$E{[X-E(X)][Y-E(Y)]}$存在,则称其为$X$和$Y$的协方差,记为$Cov(X,Y)$
- ==公式==
$$ Cov(X,Y)=E(XY)-E(X)E(Y) $$
性质
- $Cov(X,X)=D(X)$
- $Cov(X,Y)=Cov(Y,X)$
- $Cov(aX,bY)=abCov(X,Y)$
- $Cov(C,X)=0$
- $Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)$
- 当$X$与$Y$相互独立时,$Cov(X,Y)=0$
- $D(aX+bY)=a^2D(X)+b^2D(Y)+2abCov(X,Y)$
相关系数
定义
设$(X,Y)$为二维随机变量,$D(X)>0,D(Y)>0$,称 $$ \cfrac{Cov(X,Y)}{\sqrt{D(X)D(Y)}} $$ 为$X$和$Y$的相关系数,记为$\rho_{XY}$。其值为 0 时,$X$和$Y$不相关
性质
$|\rho_{XY}|\le 1$
当$X$与$Y$相互独立时,$\rho_{XY}=0$,$X$和$Y$不相关
若$D(X)>0,D(Y)>0,|\rho_{XY}|=1\Leftrightarrow 存在常数 a,b,使得 P{Y=aX+b}=1$
而且当$a>0$时,$\rho_{XY}=1$,当$a<0$时,$\rho_{XY}=-1$
==相关系数刻画了随机变量$X$与$Y$之间”线性相关“的程度==
例
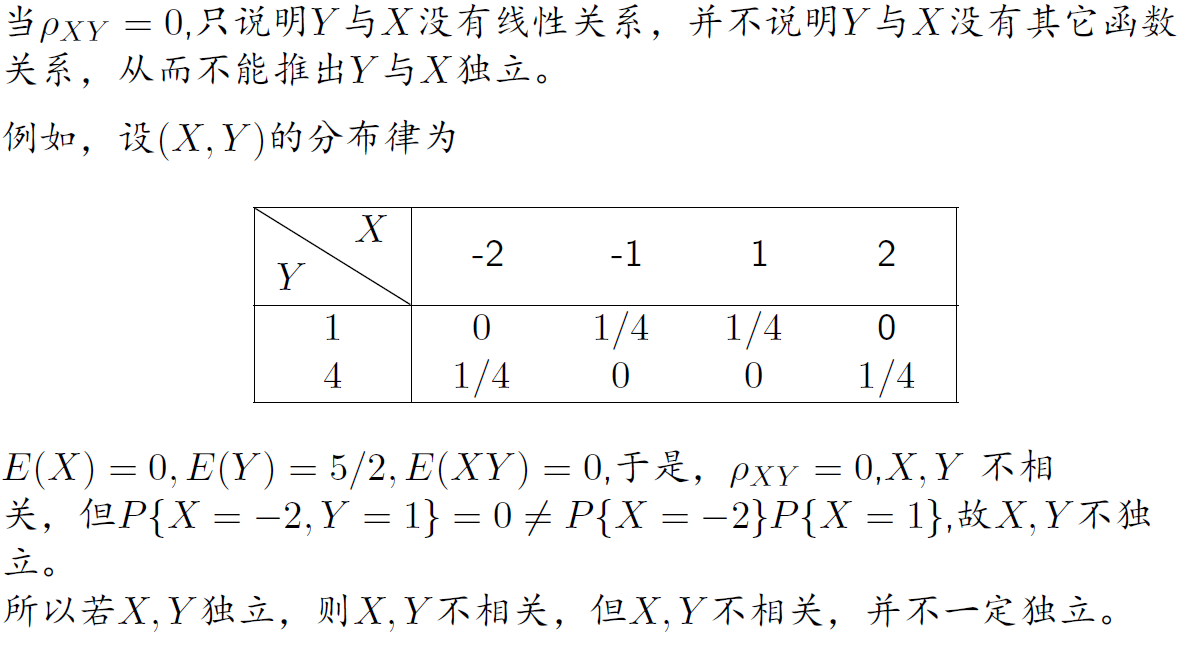
- $X^*=\cfrac{X-E(X)}{\sqrt{D{X}}}$是对随机变量$X$的标准化,有
$$ \rho_{XY}=Cov(X^,Y^) $$
- 对于二维正态分布来说,不相关$\Leftrightarrow$独立
例


不相关与独立
独立:没有任何关系
不相关:没有线性关系
$独立 \Rightarrow 不相关 \ 不相关 \nRightarrow 独立$
二维随机变量中,两者等价
矩
定义
设$X,Y$是随机变量
- 若$E(X^k),k=1,2,\ldots$存在,称它为$X$的$k$阶原点矩,简称**$k$阶矩**
- 若$E{[X-E(X)]^k},k=2,3,\ldots$存在,称它为$X$的**$k$阶中心矩**
- 若$E(X^kY^l),k,l=1,2,\ldots$存在,称它为$X$和$Y$的**$k+l$阶混合矩**
- 若$E{[X-E(X)]^k[Y-E(Y)]^l},k,l=2,3,\ldots$存在,称它为**$X$和$Y$的$k+l$阶混合中心矩**
数学期望为一阶原点矩,方差为二阶中心矩,协方差为二阶混合中心矩
协方差矩阵
设$n$维随机变量$(X_1,X_2,\ldots,X_n)$的二阶混合中心矩$E{[X_i-E(X_i)][Y_j-E(Y_j)]}\triangleq c_{i,j}, (i,j=1,2,\ldots,n)$都存在,则称矩阵 $$ \begin{pmatrix} c_{11}&c_{12}&\ldots&c_{1n} \ c_{21}&c_{22}&\ldots&c_{nn}\ \vdots&\vdots&\vdots&\vdots \ c_{n1}&c_{n2}&\ldots&c_{nn} \end{pmatrix} $$ 为$n$维随机变量$(X_1,X_2,\ldots,X_n)$的协方差矩阵