概率论 第三章
多维随机变量及其分布
二维随机变量
定义
设$E$是一个随机试验,它的样本空间为$S$,设$X=X(e), Y=Y(e)$是定义在$S$上的两个随机变量,由它们构成的向量$(X,Y)$,叫做二维随机变量(也称随机矢量)

分布函数及其性质
设$(X,Y)$是一个二维随机变量,对任意的实数$x,y$,定义 $$ F(x,y)=P({X\le x}\cap {Y\le y})\triangleq P{X\le x,Y\le y} $$ 则称$F(x,y)$为二维随机变量$(X,Y)$的分布函数。
- 性质
- $F(x,y)$是关于变量 x 和 y 的不减函数
- $0\le F(x,y)\le 1$
- $F(-\infty,y)=\lim\limits_{x\rightarrow-\infty}F(x,y)=0,\quad F(x,-\infty)=\lim\limits_{y\rightarrow-\infty}F(x,y)=0\ F(-\infty,-\infty)=\lim\limits_{x,y\rightarrow-\infty}F(x,y)=0\ F(+\infty,+\infty)=\lim\limits_{x,y\rightarrow+\infty}F(x,y)=1$
- $F(x,y)$既关于 x 右连续($F(x+0,y)=F(x,y)$),也关于 y 右连续($F(x,y+0)=F(x,y)$)
二维离散型随机变量及其分布
若二维随机变量$(X,Y)$只有有限或可列个取值对,则称$X,Y$为一个二维离散型随机变量
若随机矢量$(X,Y)$所有可能取值对为$(x_i,y_i),(i=1,2,\ldots,j=1,2,\ldots)$
则称 $$ P({X=x_i}\cap{Y=y_i})\triangleq {X=x_i,Y=y_i}=P_{i,j} \(i=1,2,\ldots,j=1,2,\ldots) $$ 为$(X,Y)$的分布律或称联合分布律。
联合分布律可以更直观地用以下表格的形式来描述

其中$p_{i,j}(i=1,2,\ldots,j=1,2,\ldots)$要满足以下条件
- $p_{i,j}\ge 0$
- $\sum\limits_{i=1}^\infty\sum\limits_{j=1}^\infty p_{i,j}=1$

二维连续型随机变量及其概率密度
二维连续型随机变量的定义
设$(X,Y)$为二维随机变量,$F(x,y)$为其分布函数,若存在一个非负二元
函数$f(x,y)$,使得对任意$x,y$有 $$ F(x,y)=\int_{-\infty}^x\int_{-\infty}^y f(s,t)dsdt $$ 则称$(X,Y)$为二维连续型随机变量,并称$f(x,y)$为$(X,Y)$的概率密度,
或称为$X$和$Y$的联合概率密度
二维概率密度的性质
- $f(x,y)\ge 0$
- $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y)dxdy=1$
- $P{(X,Y)\in D}=\iint\limits_D f(x,y)dxdy$(其中的$D$为一个平面区域)
- $f(x,y)=\cfrac{\partial ^2 F(x,y)}{\partial x\partial y}$
两个常见的二维连续型随机变量
二维均匀分布
$(X,Y)$的概率密度为 $$ f(x,y)=\begin{cases} \ \cfrac{1}{A}\qquad (x,y)\in G \ \ 0\qquad \quad 其他 \end{cases}\quad \其中 G 为平面上的一个有界区域,A 为其面积(即 S(G)) $$
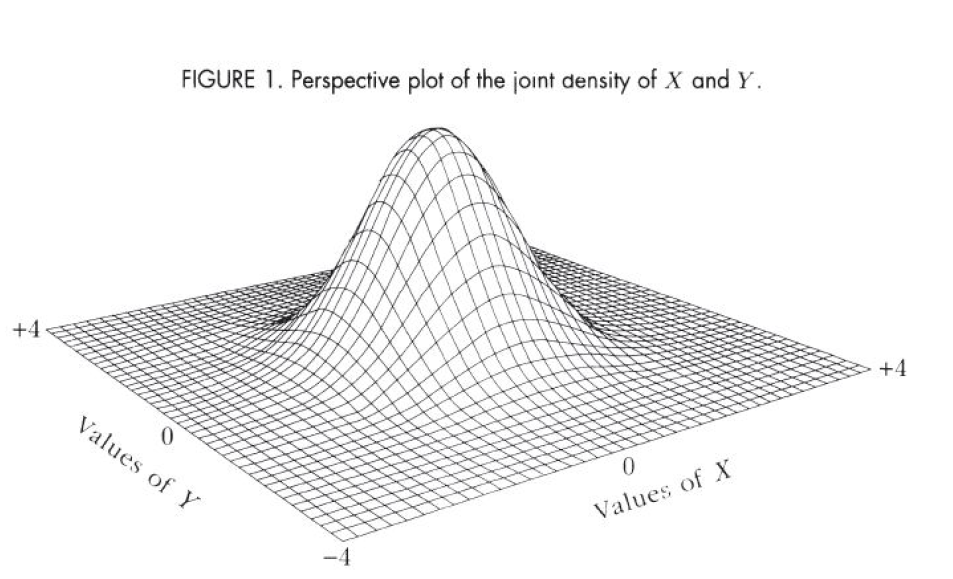
二维正态分布
$(X,Y)$的概率密度为 $$ f(x,y)=\cfrac{1}{2\pi \sqrt{1-\rho^2}\sigma_1\sigma_2}exp{\cfrac{-1}{2(1-\rho^2)}\left[ \bigg(\cfrac{x-\mu_1}{\sigma_1}\bigg)^2-2\rho \bigg(\cfrac{x-\mu_1}{\sigma_1}\bigg)\cdot \bigg(\cfrac{y-\mu_2}{\sigma_2}\bigg)+\bigg(\cfrac{y-\mu_2}{\sigma_2}\bigg)^2 \right]} $$
记作$(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$


边缘分布
(Marginal Distribution)
概念
对于二维随机变量 w$(X,Y)$,其分布函数为 $F(x,y)$,它的每个分量 $X$ 和 $Y$ 都是一维随机变量,它们各自的分布函数分别为 $F_X(x)$ 和 $F_Y(y)$,通常把它们称为 $(X,Y)$ 关于 $X$ 和 $Y$ 的边缘分布函数。
接下来我们考察一下联合分布函数$F(x,y)$与边缘分布函数$F_X(x)$和$F_Y(y)$的关系: $$ F_X(x)=P{X\le x}=P{X\le x,Y<+\infty}=F(x,+\infty)\F_Y(y)=P{Y\le y}=P{X< +\infty,Y\le y}=F(+\infty,y) $$
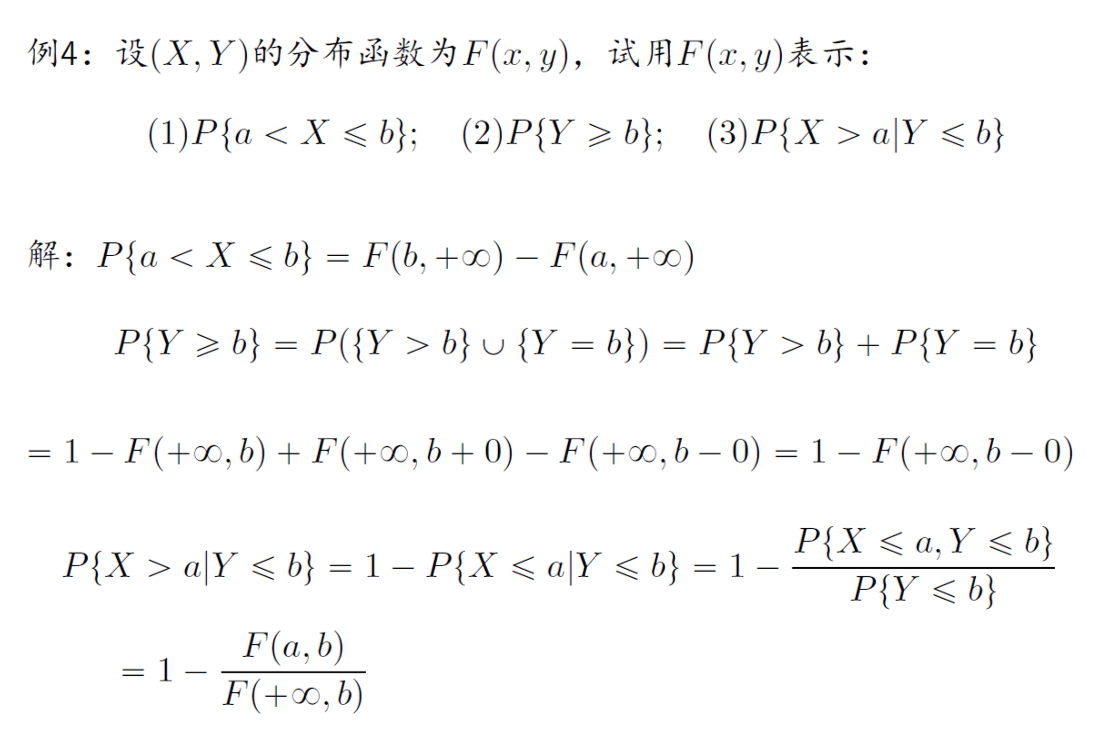
二维离散型随机变量的边缘分布律
$$ F_X(x)=F(x,+\infty)=\sum\limits_{x_i\le x}\sum\limits_{j=1}^{+\infty}p_{i,j} $$
(注意:对一维随机变量$X$,$F_X(x)=\sum\limits_{x_i\le x}p_i$)
所以关于$X$的边缘分布律为 $$ P{X=x_i}=\sum\limits_{j=1}^\infty p_{i,j}\triangleq p_{i\cdot} \qquad(i=1,2,\ldots) $$ 类似地,关于$Y$的边缘分布律为 $$ P{Y=y_i}=\sum\limits_{i=1}^\infty p_{i,j}\triangleq p_{j\cdot} \qquad(j=1,2,\ldots) $$
二维连续型随机变量的边缘概率密度

设二维连续型随机变量$(X,Y)$的联合概率密度为$f(x,y)$,则 $$ F_X(x)=F(x,+\infty)=\int_{-\infty}^x\left[ \int_{-\infty}^{+\infty}f(s,t)dt \right]ds \ 对一维连续型随机变量 X,F_X(x)=\int_{-\infty}^{x}f_X(t)dt $$ 所以,==关于$X$的边缘概率密度==为 $$ f_X(x)=\int_{-\infty}^{+\infty}f(x,y)dy $$ 同样地,==关于 $Y$ 的边缘概率密度==为 $$ f_Y(y)=\int_{-\infty}^{+\infty}f(x,y)dx $$
例

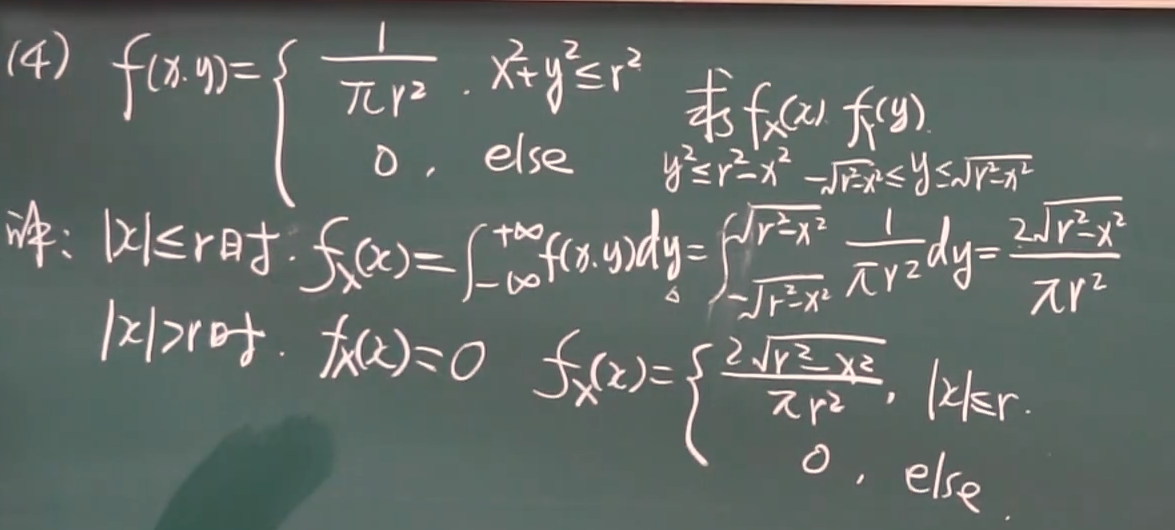
条件分布
(Conditional Distribution)
二维离散型随机变量的条件分布律
设$(X,Y)$是二维离散型随机变量,其分布律为 $$ P{X=x_i,Y=y_i}=p_{i,j}\qquad i,j=1,2,\ldots $$ 的概率,即求事件 $$ {X=x_i|Y=y_i}\qquad i=1,2,\ldots $$ 的概率。由条件概率公式可得 $$ P{X=x_i|Y=y_i}=\cfrac{P{X=x_i,Y=y_i}}{P{Y=y_i}}=\cfrac{p_{i,j}}{\sum\limits_{i=1}^{\infty}p_{i,j}}\qquad i=1,2,\ldots $$ 其为在$Y=y_i$的条件下随机变量$X$的==条件分布律==
类似地,称 $$ P{Y=y_i|X=x_i}=\cfrac{P{X=x_i,Y=y_i}}{P{X=x_i}}=\cfrac{p_{i,j}}{\sum\limits_{j=1}^{\infty}p_{i,j}}\qquad j=1,2,\ldots $$ 为在$X=x_i$的条件下随机变量$Y$的条件分布律
二维连续型随机变量的条件概率密度
考的不多
联合密度比边缘密度
称 $$ f_{X|Y}(x|y)=\cfrac{f(x,y)}{f_Y(y)} $$
为在$Y=y$条件下$X$的==条件概率密度==,记为$f_{X|Y}(x|y)$
同时称 $$ F_{X|Y}(x|y)=\int_{-\infty}^x\cfrac{f(s,y)}{f_Y(y)}ds=\int_{-\infty}^xf_{X|Y}(x|y)dx $$
为在$Y=y$条件下$X$的==条件分布函数==,记为$F_{X|Y}(x|y)$或$P{X\le x|Y=y}$
类似地,定义 $$ f_{Y|X}(y|x)=\cfrac{f(x,y)}{f_Y(x)}\ F_{Y|X}(y|x)=\int_{-\infty}^y\cfrac{f(x,t)}{f_X(x)}dt $$ 例


随机变量的独立性
二个随机变量独立性的概念
联合密度 = 边缘密度相乘
边缘密度 = 条件密度
设$F(x,y),F_X(x),F_Y(y)$分别为二维随机变量$(X,Y)$的联合分布函数和边缘分布函数,若对任意的$x,y$,都有 $$ F(x,y)=F_X(x)F_Y(y) \quad 即\ P{X\le x,Y\le y}=P{X\le x}P{Y\le y} $$
==独立的条件==
- 离散型:$P{X= x_i,Y= y_j}=P{X= x_i}P{Y= y_j}$ 对任意 i, j 成立
- 连续型:$f(x,y)=f_X(x)f_Y(y)$
例
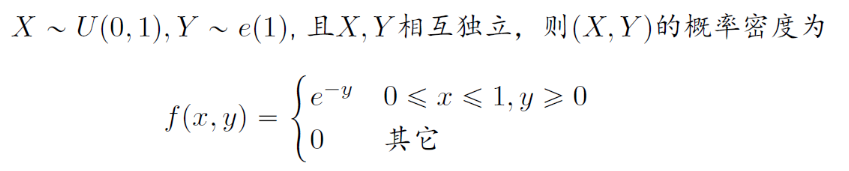
对于连续型随机变量$(X,Y)$,若$X$与$Y$相互独立,当且仅当 $$ f_X(x)=f_{X|Y}(x|y) \ 或 \ f_Y(y)=f_{Y|X}(y|x) $$ 若$(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$,则 $$ f_X(x)=\cfrac{1}{\sqrt{2\pi}\sigma_1}e^{-\cfrac{(x-\mu_1)^2}{2\sigma_1^2}},\quad f_X(x)=\cfrac{1}{\sqrt{2\pi}\sigma_2}e^{-\cfrac{(x-\mu_2)^2}{2\sigma_2^2}} $$ 对于二维正态随机变量$(X,Y)$,相互独立的充要条件为 $\rho=0$
多维随机变量的独立性
$n$维随机变量$(X_1,X_2,\ldots ,X_n)$的分布函数定义为 $$ F(x_1,x_2,\ldots,x_n)=P{X_1\le x_1,X_2\le x_2,\ldots,X_n\le x_n} $$ 若对于所有$x_1,x_2,\ldots,x_n$,有 $$ F(x_1,x_2,\ldots,x_n)=F_{X_1}(x_1)F_{X_2}(x_2)\ldots F_{X_n}(x_n) $$ 则称$X_1,X_2,\ldots ,X_n$是相互独立的
两个随机变量的函数的分布
二维连续型随机变量的函数的分布
一般的二维连续型随机变量的函数的分布
设$(X,Y)$是二维随机变量,其概率密度为$f(x,y)$,$Z=g(X,Y)$是一个二维随机变量的函数,==则== $$ F_Z(z)=P{Z\le z}=P{g(X,Y)\le z}=\iint\limits_{D_z} f(x,y)dxdy \ 其中 D_z={(x,y)|g(x,y)\le z} $$ 例

$Z=X+Y$的分布
设$(X,Y)$是二维随机变量,其概率密度为$f(x,y)$,则$Z=X+Y$的分布函数为 $$ F_Z(z)=\int_{-\infty}^z[\int_{-\infty}^{+\infty}f(u-y,y)dy]du $$ 其概率密度为 $$ f_{X+Y}(z)=\int_{-\infty}^{+\infty}f(z-y,y)dy=\int_{-\infty}^{+\infty}f(x,z-x)dx $$
例

$Z=\cfrac{Y}{X},Z=XY$的分布
设$(X,Y)$是二维随机变量,其概率密度为$f(x,y)$,则$Z=\cfrac{Y}{X}$的分布函数为 $$ f_{\frac{Y}{X}}(z)=\int_{-\infty}^{+\infty}|x|f(x,xz)dx $$ 也可以求得$Z=XY$的概率密度为 $$ f_{XY}(z)=\int_{-\infty}^{+\infty}\cfrac{1}{|x|}f(x,\cfrac{z}{x})dx $$
$M=max{X,Y},N=min{X,Y}$ 的分布
设 $(X,Y)$ 是二维随机变量,其概率密度为 $f(x,y)$,则 $M=max{X,Y}$ 的分布函数为 $$ F_{max}(z)=F_X(z)F_Y(z) $$ $N=min{X,Y}$ 的分布函数为 $$ F_{min}(z)=1-[1-F_X(z)][1-F_Y(z)] $$
扩展
设$X_i(i=1,2,\ldots,n)$是$n$个相互独立的随机变量,它们的分布函数为$F_{x_i}(x)$,则$M=max{X_1,X_2,\ldots,X_n}$和$N=min{X_1,X_2,\ldots,X_n}$的分布函数分别为
$$ F_{max}(z)=F_{x_1}(z)F_{x_2}(z)\ldots F_{x_n}(z) \ \qquad \ F_{min}(z)=1-[1-F_{x_1}(z)][1-F_{x_2}(z)]\ldots [1-F_{x_n}(z)] $$
例
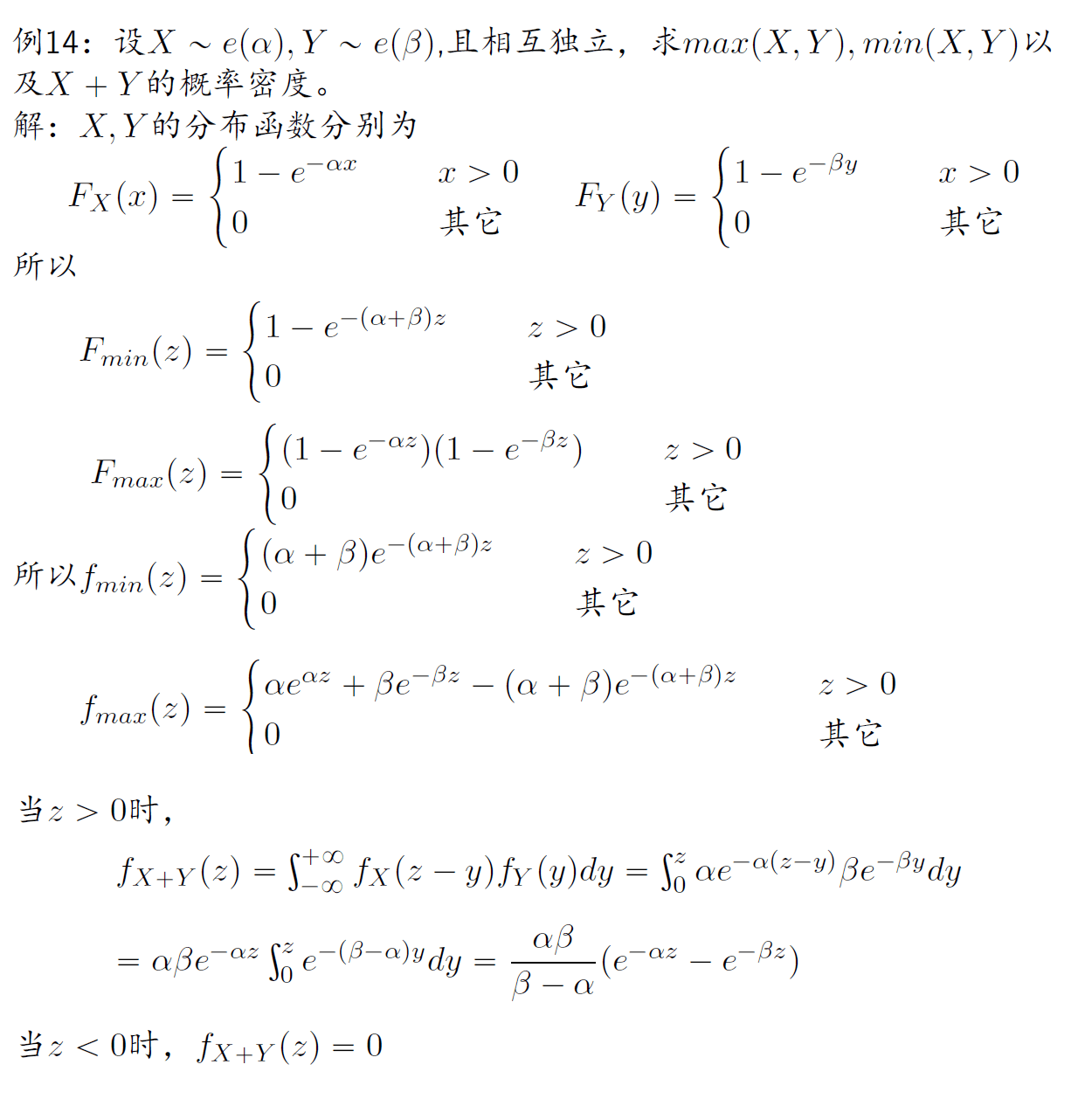
二维离散型随机变量的函数的分布
- 注意:若$X$和$Y$相互独立
- 若$X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$,则$X+Y\sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$
- 若$X\sim e(\alpha),Y\sim e(\beta)$,则$min(X,Y)\sim e(\alpha+\beta)$
- 若$X\sim B(n_1,p),Y\sim B(n_2,p)$,则$Z=X+Y\sim B(n_1+n_2,p)$
- 若$X\sim \pi(\lambda_1),Y\sim \pi(\lambda_2)$,则$Z=X+Y\sim \pi(\lambda_1+\lambda_2)$