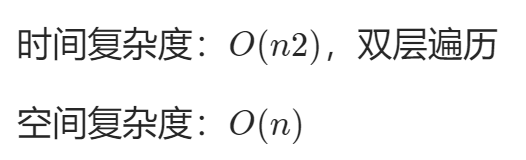300. 最长递增子序列

mid

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

1
2
3
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

1
2
输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

1
2
输入：nums = [7,7,7,7,7,7,7]
输出：1

DP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
func lengthOfLIS(nums []int) int {
	res := 1
	dp := make([]int, len(nums))
	dp[0] = 1
	for i := 1; i < len(nums); i++ {
		maxLen := 0
		for j := 0; j < i; j++ {
			if nums[j] < nums[i] && dp[j] > maxLen {
				maxLen = dp[j]
			}
		}
		dp[i] = maxLen + 1
		if dp[i] > res {
			res = dp[i]
		}
	}
	return res
}	

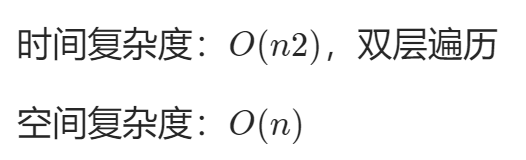
DP + 二分

很具小巧思。新建数组 dp，用于保存最长上升子序列。

对原序列进行遍历，将每位元素二分插入 dp 中。

如果 dp 中元素都比它小，将它插到最后
否则，用它覆盖掉比它大的元素中最小的那个。

总之，思想就是让 dp 中存储比较小的元素。这样，dp 未必是真实的最长上升子序列，但长度是对的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func lengthOfLIS(nums []int) int {
	if len(nums) == 1 {
		return 1
	}
	dp := []int{nums[0]}
	for i := 1; i < len(nums); i++ {
		// nums[i] 最大
		if nums[i] > dp[len(dp)-1] {
			dp = append(dp, nums[i])
			continue
		}
		low, high := 0, len(dp)-1
		for low <= high {
			mid := low + (high-low)>>1
			if nums[i] <= dp[mid] {
				if mid==0||nums[i] > dp[mid-1] {
					// 找到第一个大于等于nums[i]的元素
					dp[mid] = nums[i] // 替换
					break
				}
                high = mid - 1
			} else {
				low = mid + 1
			}
		}
	}
	return len(dp)
}

这样时间复杂度能降低到 $O(nlogn)$

DFS

超时了，他妈的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
func lengthOfLIS(nums []int) int {
	res := 1
	var dfs func(startIndex, lastVal, curLen int)
	dfs = func(startIndex, lastVal, curLen int) {
		if curLen > res {
			res = curLen
		}
		if startIndex == len(nums) {
			return
		}
		for i := startIndex; i < len(nums); i++ {
			if nums[i] > lastVal && curLen+len(nums)-i > res {
				dfs(i+1, nums[i], curLen+1)
			}
		}
	}
	for i := 1; i < len(nums); i++ {
		dfs(i, nums[i-1], 1)
	}
	return res
}