221. 最大正方形

mid

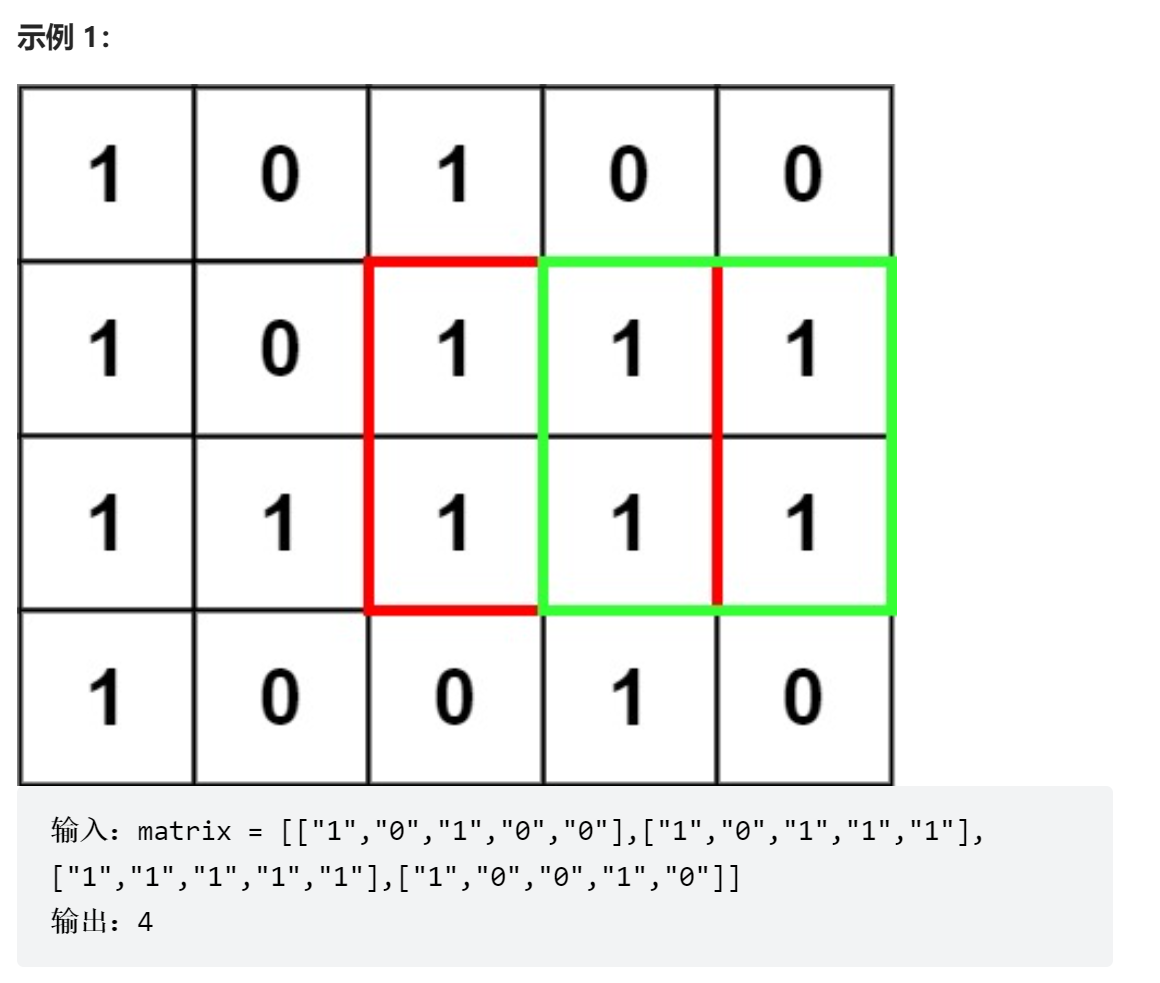
在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

DP

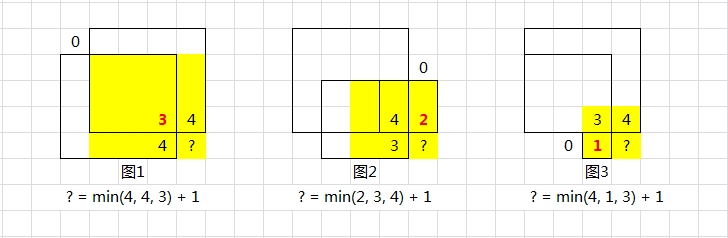
若某格子值为 1，则以此为右下角的正方形的、最大边长为：上面的正方形、左面的正方形或左上的正方形中，最小的那个，再加上此格。 $$ dp(i, j) = min(dp(i - 1, j), dp(i, j - 1), dp(i - 1, j - 1)) + 1; $$ 这个转移方程比较神奇，感受一下就好

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func maximalSquare(matrix [][]byte) int {
	rows, cols := len(matrix), len(matrix[0])
	dp := make([][]int, rows)
	for i := 0; i < rows; i++ {
		dp[i] = make([]int, cols)
	}
	maxSideLen := 0
	// 先给第0行和第0列赋值
	for y := 0; y < cols; y++ {
		if matrix[0][y] == '1' {
			dp[0][y] = 1
			maxSideLen = 1
		} else {
			dp[0][y] = 0
		}
	}
	for x := 0; x < rows; x++ {
		if matrix[x][0] == '1' {
			dp[x][0] = 1
			maxSideLen = 1
		} else {
			dp[x][0] = 0
		}
	}
	for x := 1; x < rows; x++ {
		for y := 1; y < cols; y++ {
			if matrix[x][y] == '1' {
				dp[x][y] = min(dp[x-1][y-1], min(dp[x-1][y], dp[x][y-1])) + 1
				if dp[x][y] > maxSideLen {
					maxSideLen = dp[x][y]
				}
			}
		}
	}
	return maxSideLen * maxSideLen
}

func min(a, b int) int {
	if a < b {
		return a
	} else {
		return b
	}
}