剑指 Offer 13. 机器人的运动范围

mid

地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。

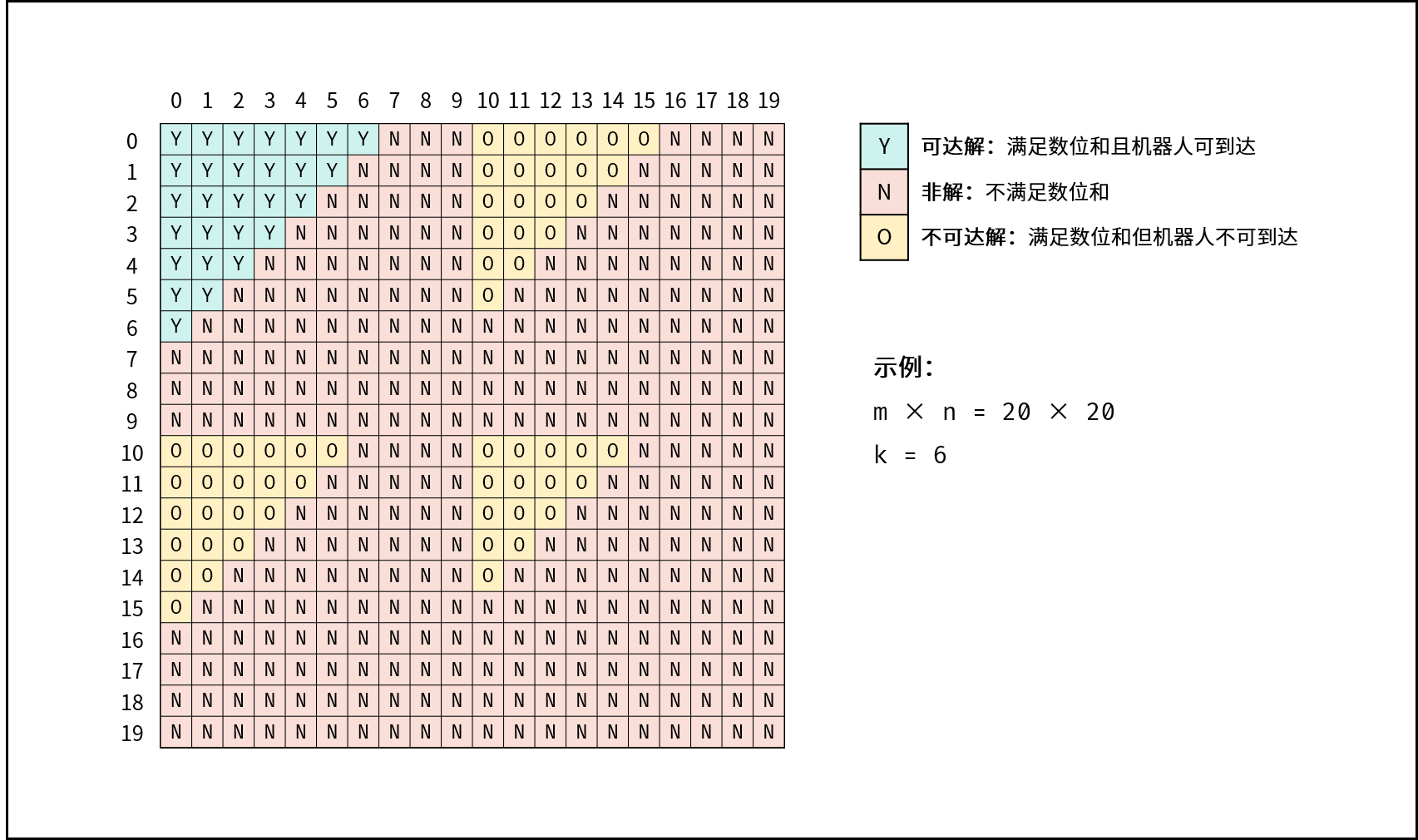
一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于 k 的格子。

例如，当 k 为 18 时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。

请问该机器人能够到达多少个格子？

示例 1：

1
2
输入：m = 2, n = 3, k = 1
输出：3

示例 2：

1
2
输入：m = 3, n = 1, k = 0
输出：1

分析

题目特点：

无论是 DFS 还是 BFS，向右和向下走就能覆盖所有位置
可达范围呈三角形状

各位之和算法：

1
2
3
4
5
6
7
8
// 获取各位数之和
func getSum(num int) (res int) {
	for num != 0 {
		res += num % 10
		num /= 10
	}
	return
}

DFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// DFS
func movingCount(m int, n int, k int) int {
	visited := make([][]bool, m) // 存储已遍历过的坐标
	for i, _ := range visited {
		visited[i] = make([]bool, n)
	}
	res := 0
	var backtracking func(i, j int)
	backtracking = func(i, j int) {
		if i < 0 || i > m-1 || j < 0 || j > n-1 {
			// 越界
			return
		}
		if visited[i][j] {
			// 已被遍历过
			return
		}
		visited[i][j] = true
		if getSum(i)+getSum(j) <= k {
			res++
			backtracking(i+1, j) // 下
			backtracking(i, j+1) // 右
		}
	}
	backtracking(0, 0)
	return res
}

BFS

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// BFS
func movingCount2(m int, n int, k int) int {
	visited := make([][]bool, m) // 存储已遍历过的坐标
	for i, _ := range visited {
		visited[i] = make([]bool, n)
	}

	res := 0
	stack := list.New()
	stack.PushBack([2]int{0, 0})

	var curPos [2]int
	var i, j int
	for stack.Len() != 0 {
		// 出栈
		curPos = stack.Front().Value.([2]int)
		stack.Remove(stack.Front())
		i, j = curPos[0], curPos[1]
		if i < 0 || i > m-1 || j < 0 || j > n-1 {
			// 越界
			continue
		}
		if visited[i][j] {
			// 已经遍历过
			continue
		}
		visited[i][j] = true
		if getSum(i)+getSum(j) <= k {
			res++
			// 右边和下边入队
			stack.PushBack([2]int{i + 1, j})
			stack.PushBack([2]int{i, j + 1})
		}
	}
	return res
}

DP

位置 i, j 是否可达取决于：

i-1, j 或 i,j-1 任意一个是否可达
i, j 位数和是否小于等于 k

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
// dp
func movingCount3(m int, n int, k int) int {
	visited := make(map[[2]int]bool)
	visited[[2]int{0, 0}] = true
	res := 1
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if getSum(i)+getSum(j) <= k && (visited[[2]int{i - 1, j}] || visited[[2]int{i, j - 1}]) {
				res++
				visited[[2]int{i, j}] = true
			}
		}
	}
	return res
}