78. 子集

mid

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

1
2
输入：nums = [0]
输出：[[],[0]]

DFS

经典的组合问题，一棵二叉树，选或不选

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
func subsets(nums []int) [][]int {
	res := make([][]int, 0)
	var dfs func(subset []int, layer int)
	dfs = func(subset []int, layer int) {
		if layer == len(nums) {
			subsetCopy := make([]int, len(subset))
			copy(subsetCopy, subset)
			res = append(res, subsetCopy)
			return
		}
		dfs(subset, layer+1)
		dfs(append(subset, nums[layer]), layer+1)
	}
	dfs([]int{},0)
	return res
}

更标准的 DFS 回溯写法

然而内存消耗并没有区别。。。

其实这道题是用不上回溯的

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
func subsets(nums []int) [][]int {
	res := make([][]int, 0)
	subset := make([]int, 0)
	var dfs func(layer int)
	dfs = func(layer int) {
		if layer == len(nums) {
			subsetCopy := make([]int, len(subset))
			copy(subsetCopy, subset)
			res = append(res, subsetCopy)
			return
		}
		dfs(layer + 1)
		subset = append(subset, nums[layer])
		dfs(layer + 1)
		subset = subset[:len(subset)-1]
	}
	dfs(0)
	return res
}

这样写切片拷贝，好像更快一点：

1
res = append(res, append([]int{}, subset...))

另一种思路

之前的思路是收集一棵树所有的叶子节点，也可以收集树的所有节点

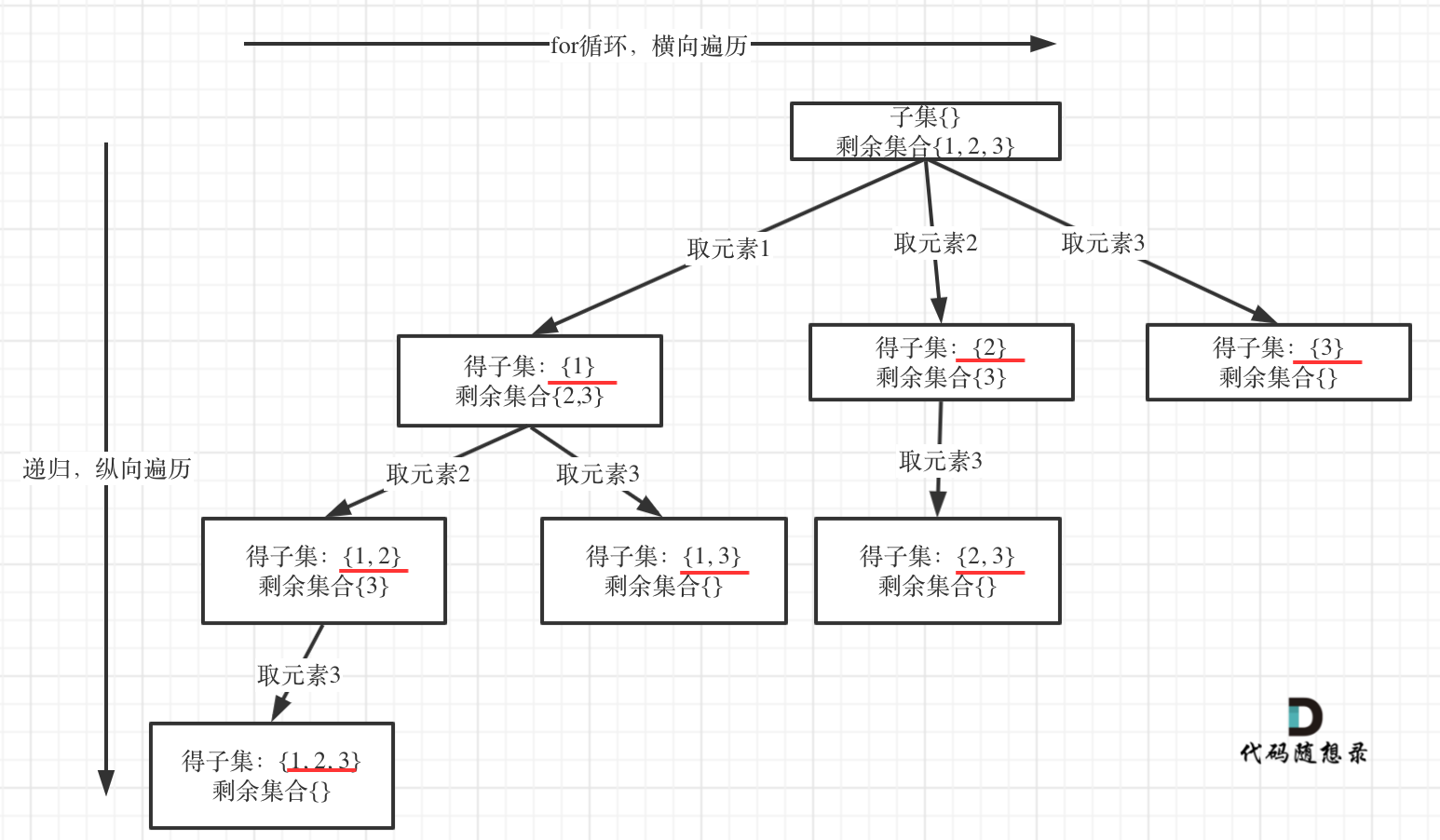
这样的话就有一个 for 循环选取剩余集合中的每个元素了，用 startIndex 避免重复（因为是组合问题）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
func subsets(nums []int) [][]int {
	res := make([][]int, 0)
	var dfs func(subset []int, startIndex int)
	dfs = func(subset []int, startIndex int) {
		res = append(res, append([]int{}, subset...))
		if startIndex == len(nums) {
			// 终止条件 可以不加
			return
		}
		for i := startIndex; i < len(nums); i++ {
			subset = append(subset, nums[i])
			dfs(subset, i+1)
			subset = subset[:len(subset)-1]
		}
	}
	dfs([]int{}, 0)
	return res
}

这才是真回溯