54. 螺旋矩阵
mid
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:

1
2
| 输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
|
示例 2:

1
2
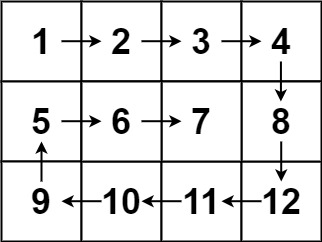
| 输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
|
模拟
就恩写;注意边界条件
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| func spiralOrder(matrix [][]int) []int {
m, n := len(matrix), len(matrix[0])
res := make([]int, m*n)
if n == 1 {
for i, x := range matrix {
res[i] = x[0]
}
return res
}
layer := 0 // 当前层
i, j := 0, 0 // 行列指针
state := 'r'
count := 0
for count < m*n {
if state == 'r' {
res[count] = matrix[i][j]
j++
if j+1 == n-layer {
state = 'd'
}
if j+1 > n-layer {
// 溢出后的处理
j = n - layer - 1
i++
}
} else if state == 'd' {
res[count] = matrix[i][j]
i++
if i+1 == m-layer {
state = 'l'
}
if i+1 > m-layer {
i = m - layer - 1
j--
}
} else if state == 'l' {
res[count] = matrix[i][j]
j--
if j == layer {
state = 'u'
}
if j < layer {
j = layer
i--
}
} else if state == 'u' {
res[count] = matrix[i][j]
i--
if i == layer {
state = 'r'
layer++
i++
j++
}
}
count++
fmt.Println(res)
}
return res
}
|
更好的模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| func spiralOrder(matrix [][]int) []int {
if len(matrix) == 0 {
return []int{}
}
m, n := len(matrix), len(matrix[0])
res := make([]int, m*n)
l, r, t, b := 0, n-1, 0, m-1 // 左右上下
count := 0
state := 'r'
for count < m*n {
if state == 'r' {
// l2r
for col := l; col <= r; col++ {
res[count] = matrix[t][col]
count++
}
t++
state = 'd'
} else if state == 'd' {
// u2d
for row := t; row <= b; row++ {
res[count] = matrix[row][r]
count++
}
r--
state = 'l'
} else if state == 'l' {
// r2l
for col := r; col >= l; col-- {
res[count] = matrix[b][col]
count++
}
b--
state = 'u'
} else if state == 'u' {
// d2u
for row := b; row >= t; row-- {
res[count] = matrix[row][l]
count++
}
l++
state = 'r'
}
}
return res
}
|